Помехозащищенность цифрового вольтметра, страница 5

Физически это можно представить таким образом: конденсаторы в схеме на рис. 13,а разряжены, напряжение на емкости не может изменится скачком;

2) ; h(0)=1, т.е. .

Это можно представить так: конденсаторы в схеме на рис. 13,а полностью зарядились и поэтому их можно не учитывать.

Переходная функция h(t) показана на рис. 13,г. пунктиром показаны 2-е и 3-е слагаемые правой части (27). Экспонента с постоянной времени 0,85 мс сравнительно быстро затухает, поэтому для времен, расположенных на рис. 13 правее штрихпунктирной вертикали, вместо (27) можно записать

.

Соответственно относительная погрешность, связанная с тем, что экспонента не достигает асимптоты, будет

.

Задавшись условием, что эта погрешность не должна превосходить относительной значения кванта ЦВ, получим

,

откуда

.

При =12 мс имеем, в миллисекундах,

.

С использованием последней формулы, а также (18), (19), (23) получены данные, помещенные в табл. 1, из которой явно видно преимущество двойного Т-образного RC-фильтра (2ТФ) по сравнению с простым низкочастотным RC-фильтром (НЧФ) при защите от сетевой помехи

Таблица 1

Вид фильтра	, мс	f, Гц	,  дБ	, мс
НЧФ	300	50	40	2000	3500
2ТФ	6,4	50+-0,5	46	80	140

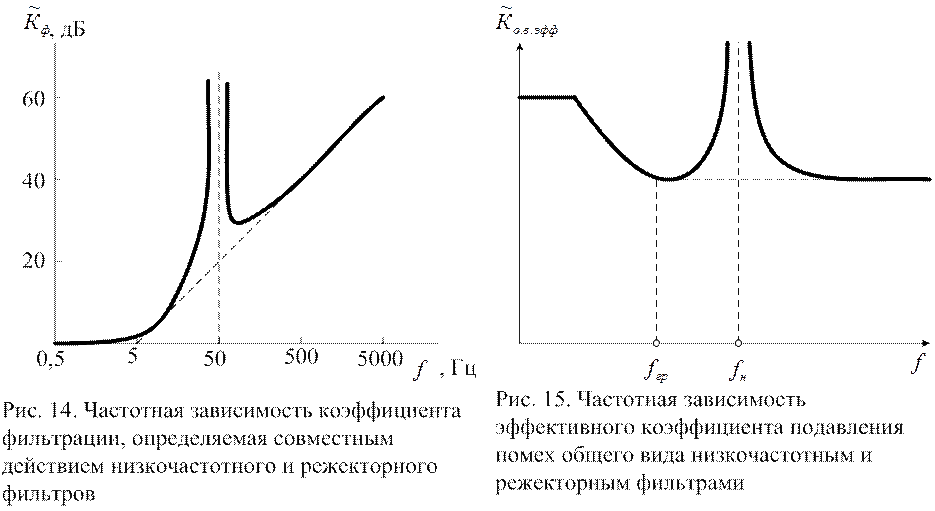
Иногда хороший режекторный фильтр сочетают с низкочастотным, чтобы обеспечить хорошую защиты от помех как сетевой частоты, так и более высокочастотных. На рис. 14 показана частотная зависимость (f) такого сложного фильтра с граничной частотой полосы пропускания низкочастотного фильтра 5  Гц и с частотой настройки режекторного фильтра 50  Гц. Иногда применяют набор режекторных фильтров. Настроенных на частоты нескольких начальных гармоник сетевого напряжения.

 Установим связь , во-первых, с коэффициентом подавления помехи , в соответствии с (1) и , во-вторых, с эффективным коэффициентом подавления помехи , в соответствии с (5). Изменение показаний ЦВ, обусловленное переменной составляющей напряжения на выходе фильтра, а в общем случае зависит не только от ее значения, но и от фазы. Для КИ ЦВ и ВИ ЦВ с разверткой в худшем случае изменение показаний , где  - амплитудное значение переменной составляющей напряжение на выходе фильтра.

 Далее нужно связать   (рис. 11) с созданной ею переменной составляющей напряжение на входе фильтра (). В общем случае . Соотношение между  и  зависит от , ,  и входного сопротивления фильтра. Здесь лучший случай -равенство  при короткой линии связи (==0) и при очень малом выходном сопротивлении источника измеряемого напряжения (=0). Подставляя в (1)  и , получаем

                                                                  

 Таким образом, в общем случае  и в худшем случае . Применяя аналогичное рассуждение по отношению к  и учитывая (6), получаем для худшего случая

                                                        

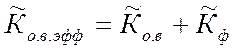
Интересно отметить, что если частотная зависимость (f) имеет вид, показанный на рис. 10 (наклон - 20 дБ/дек), и применен низкочастотный фильтр с частотной характеристикой, показанной на рис. 12,б (наклон +20 дБ/дек), то в области > происходит выравнивание частотной зависимости  (f). На рис. 15 показана более сложная зависимость (f), соответствующая сочетанию низкочастотного фильтра с режекторным. В области < =0 и (f)= (f) (горизонтальный участок, а затем спад с наклоном – 20 дБ/дек). В области > спад (f) компенсируется подъемом (f) низкочастотного фильтра. В окрестности частоты настройки  режекторного фильтра имеется резкий всплеск.

Для повышения  применяют не только RC, но и LC-фильтры, а также активные фильтры. Однако при прочих равных условиях увеличение  приводит к увеличению .

Итак, принципиальный недостаток защиты от помех нормального вида с помощью фильтров нормального вида состоит в том, что чем выше помехозащищенность ЦВ, тем больше инерционность.

2.2 Интегрирование. Идея защиты состоит в том, что интеграл от синусоидального сигнала за время, равное или краткое его периоду, равен нулю:

                                                      ,

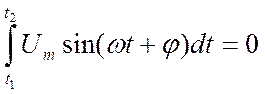если

                                                         -=kT,

где k=1,2,3…; T=2.

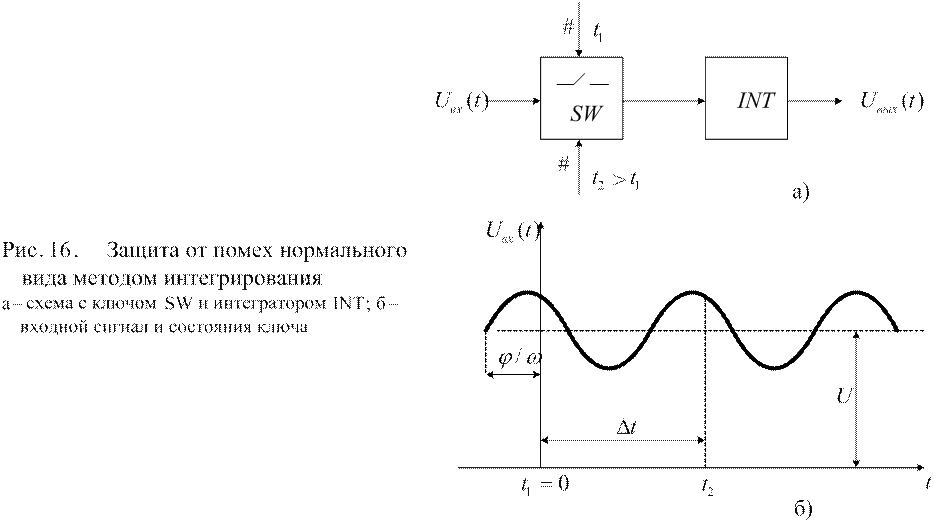
Пусть ко входу устройства (рис. 16,а), содержащего идеальный ключ SW, замыкаемый в момент  и размыкаемый в момент , и идеальный интегратор INT, приложено напряжение . Тогда после замыкания SW на выходе будет напряжение

                                            ,

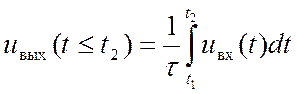где - постоянная интегрирования.

Вначале предложим, что помехи нет:

                                                         =U

где U – напряжение постоянного тока. Тогда

,

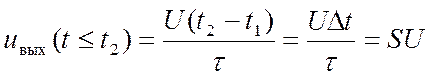где =- - длительность интегрирования; S=/ - коэффициент преобразования рассматриваемого устройства (рис. 16,а).

Предложим, что на полезный сигнал наложена синусоидальная помеха нормального вида

                                                 ,

где - фазовый сдвиг помехи относительного начала интегрирования, т.е. относительно момента , принимаемого за начало координат: =0; = (рис. 16,б).

В этом случае

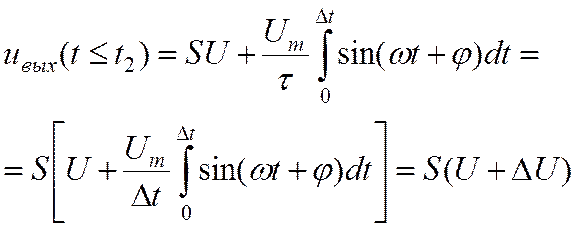                                                                              (28)

где  - приведенное ко входу изменение выходного напряжения, вызванное помехой. При

                                            =kT=2                      (29)

где k=1,2,3…,

и (28) совпадает с (27), как будто помехи нет. Однако (29) не может быть выполнено идеально точно, поэтому

                                                               

и можно говорить о коэффициенте подавления помехи нормального вида устройством, показанным на рис. 16,а

В соответствии с (1) и (28)