Обработка результатов нескольких групп прямых многократных измерений, страница 5

r	Ui ,мB	ne	Ui ,мB
1	-0,16673	2	-0,1904
2	-0,11945	3	-0,1431
3	-0,07218	6	-0,0958
4	-0,02491	39	-0,0485
5	0,022364	108	-0,0958
6	0,069636	26	0,046
7	0,116909	10	0,09327
8	0,164182	3	0,14055
9	0,211455	1	-0,0013
10	0,258727	1	0,23509
11	0,306	1	0,28236

11.4 Строим гистограмму расчетных  значений.

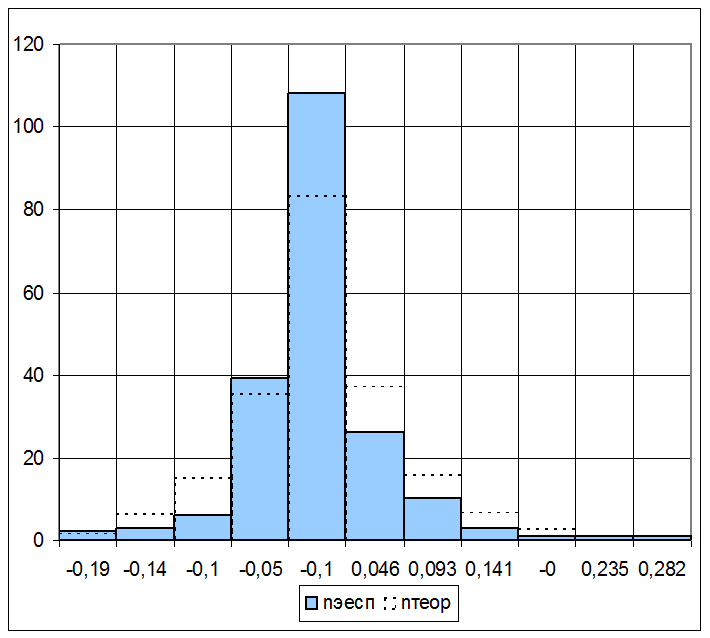
Рис.2

12. Определим вид распределения и построим теоретическую гистограмму. Расчетная гистограмма имеет один ярко выраженный максимум, поэтому стоит проверить полученное распределение на соответствие функции Лапласа, проверять на нормальное распределение не имеет смысла.

12.1  Рассчитаем аргумент функции Лапласа.

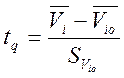
-3,866244696

-2,585

-1,7311

-0,877

-0,023

0,831

1,6851177

2,5392

3,3932

4,2473

5,101341

12.2 Определим значения функции Лапласа.

0,01047

0,0377

0,0885

0,208

0,489

0,218

0,0927113

0,0395

0,0168

0,0072

0,00304

12.3  Найдем n_t для построения теоретической гистограммы.

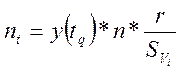   n- число результатов

5,496962

21,037006

80,50913

51,5401

15,27545

3,99147

1,04297

12.4 Определим  экспериментальное.

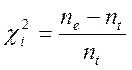
1,13423

3,8820862

13,93182

0,80966

1,821904

0,993607

0,00177

12.5 Определим  суммарное.

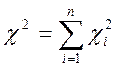
22,57507

12.6 Из таблицы распределения  определим минимальное и максимальное значения интервала.

	26,1
	1,646

12.7 Исследуемое распределение соответствует функции Лапласа, т.к.  суммарное входит в этот интервал. Распределение Лапласа принадлежит к семейству нормальных,  поэтому можно выбрать соответствующие оценки измеренных значений.

13. Аппроксимация статической характеристики преобразования

Для получения теоретической зависимости   необходимо аппроксимировать статическую характеристику преобразования. Для аппроксимации используем метод наименьших квадратов (МНК).

13.1 Находим теоретическую зависимость вида  , т.к. исходный график СХП представляет собой квадратичную зависимость, для чего составляем систему условных уравнений:

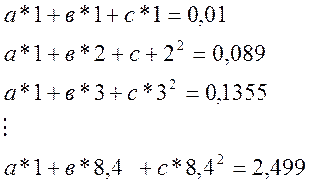
13.2 Решение системы уравнений необходимо выполнять таким образом, чтобы сумма квадратов невязок была минимальной. Использование МНК позволяет путем дифференцирования суммы квадратов невязок получить систему уравнений, для которой число неизвестных и число уравнений совпадают, эту систему можно записать в виде матрицы.

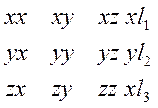
13.3 Вычислим значения элементов матрицы.

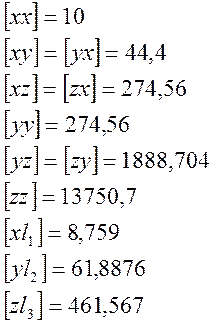
Запишем их в стандартном виде.

10	44,4	274,56	8,759
44,4	274,56	1888,704	61,8876
274,56	1888,7	13750,7	461,56744

Решая ее, получим   ,  , 

Тогда

Статическая характеристика преобразования и аппроксимирующая ее функция.

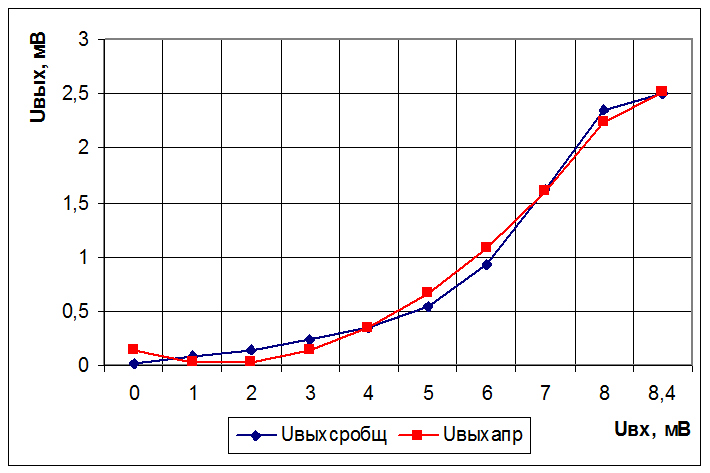
График 4

14. Аппроксимация невязок

  14.1  По полученной теоретической функции U_{вых теор} и известным значениям U_вых вычисляем невязки

0,124334

-0,06101

-0,108393

-0,1043

-0,00674

0,116295

0,154799

-0,01923

-0,11578

0,020027

14.2 С помощью МНК аппроксимируем полученную функцию прямой. 

14.3 Составим систему нормальных уравнений 

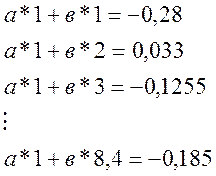
14.4 Запишем уравнения в виде матрицы и определим ее элементы.

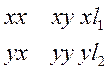
10	44,4	1,01308E-14
44,4	274,56	4,39926E-14

14.5 Получим значения коэффициентов

   

Аппроксимация невязок

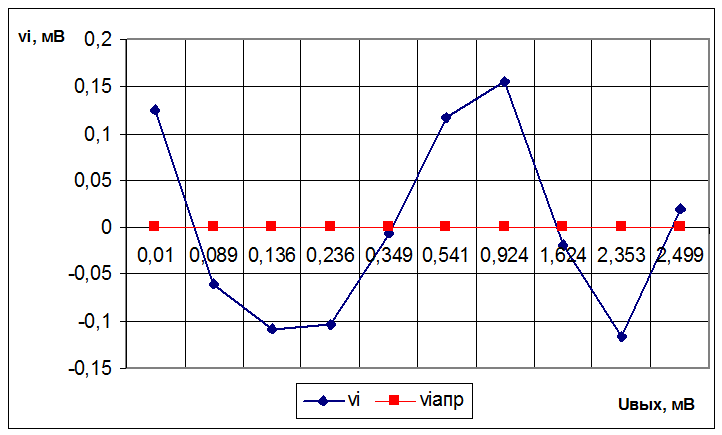
График 5

15. Вычисление доверительных интервалов аппроксимирующей функции

15.1Вычислим оценку дисперсии   условных уравнений из соотношения:

,

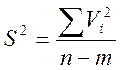где m – число искомых неизвестных, n- кол-во уравнений n = 10, m = 3

15.2 q

10	44,4	274,56	D
44,4	274,56	1888,704	325471,1
274,56	1888,7	13750,7

  

,    

Среднеквадратические отклонения характеризуют вероятную погрешность полученных значений а и в и могут быть использованы для вычисления доверительных интервалов оценок а и в:

± ,    ±,    

При Р_д = 0.99  t_s = 3,25

Тогда получим

,  ,

16. Вычисление погрешности нелинейности, погрешности  преобразователя  и его класса точности

Погрешность нелинейности вычисляем по формуле:

γ_н = ,

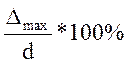где  - максимальное отклонение

     d – диапазон измерения

γ_н =

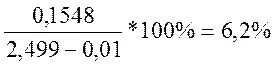
Погрешность преобразователя рассчитываем по формуле:

,

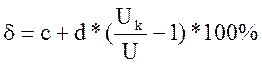где ,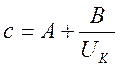

      

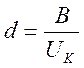
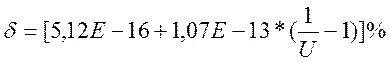
Поскольку значение с > d, то класс точности рассчитываем по формуле:

γ_кл = ;

γ_кл =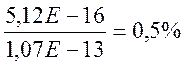

Заключение

На основании произведенных расчетов можно сделать вывод о точности измерительного преобразователя. Получено значение погрешности нелинейности. Класс точности преобразователя γ_кл = 0,5% является допустимым и позволяет использовать средство измерения для технических измерений.

Полученные результаты измерения не содержат промахов. В выделенных столбцах выявлена корреляционная зависимость с учетом ее пересчитаны СКО. Проверка на равноточность и равнорассеянность дала положительный результат, после чего измеренные значения были объединены в одну серию. Определен вид распределения погрешности как распределение Лапласа и выбраны соответствующие оценки. Аппроксимировав статическую характеристику преобразования, получили теоретическую зависимость выходного сигнала измерительного преобразователя от входного, а также получили погрешность преобразователя.

В ходе курсовой работы я научилась выявлять погрешности, освоила методы их расчета, а также научилась применять метод наименьших квадратов для получения эмпирических зависимостей.

Список используемой литературы

1. Г.Д. Бурдун, Б.М. Марков. – Основы метрологии. – М.,1975

2. П.В. Новицкий, И.А. Зограф.- Оценка погрешностей результатов измерений. - Л:. Энергоатомиздат. Ленингр. отд-ние,1991

3. Е.С. Вентцель-Теория вероятностей М.,1969

4. Е.С. Полищук- Метрология и измерительная техника. - Львов: Издательство «Бескид Бит»,2003