Обработка результатов нескольких групп прямых многократных измерений, страница 3

6. Проверка на промахи. Используем критерий Смирнова, т.к. число измеренных значений больше 100. При Рдов=0,99 tдоп=2,41

6.1  максимальное отклонение

0	0,008	0,037	0,012	0,046	0,056	0,075	0,115	0,045	0,03
0	0	0,036	0,036	0,077	0,102	0,122	0,227	0,08	0,03

6.2  Определяем tк(смещенное).

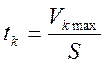
0	1,897367	1,431811	1,161895	1,621847	1,379089	1,444863	1,382768	1,979736	1,59099
0	0	1,204469	1,620811	1,760847	1,773801	1,084189	1,804583	1,798876	1,778781

если tк >= tдоп, то к- промах

если tк < tдоп, то к- нормальный результат

Промахов нет.

7.  Проверка на однородность.

Для того чтобы решить, можно ли объединить две серии измерений в одну, необходимо знать, допустимы ли расхождения средних. Для проверки на

однородность используем Т-критерий.

7.1 Определяем Т экспериментальное.

       

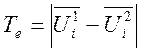
0

0,002

0,003

0,004

0,009

0,014

0,057

0,158

0,005

0,038

          7.2 Определяем Т допустимое

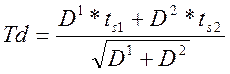
0

0

0,12841

0,079608

0,169395

0,228786

0,402747

0,490093

0,162319

0,082219

если Тэксп < Тдоп, то результаты однородные

если Тэксп > Тдоп, то результаты не однородные

Результаты однородны.

  Максимальное расхождение средних случайно, систематическая погрешность незначительна, все измерения можно объединить в серию.

8. Проверка дисперсий на равно рассеянность.

   Поскольку две группы измерений могут иметь разные рассеивания результатов, необходимо проверить, являются ли различия дисперсий случайными или присутствует их систематическое расхождение и соответственно группы нельзя признать равноточными. Проверку проводим по

критерию Фишера.

8.1 Определим Fдоп =5,35 при Рдов=0,99

8.2 Определим Fэксп

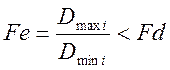
1

8,67362E-14

1,33777

4,625

2,377072

2,005391

4,699381

2,287711

3,827957

1,25

Результаты равно рассеянные.

9. Проверка на наличие корреляционной связи.

9.1 Определим Rдоп=0,735 при Рдов=0,99

9.2 Определим R

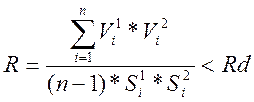
1

4,16334E-15

0,434452

0,329368

0,661145

0,622407

0,804652

0,13754

0,2638

-0,559017

В выделенной ячейке результаты коррелированны, необходимо пересчитать СКО с учетом корреляционной связи.

0

0,0421637

0,039511

0,024495

0,052122

0,070396

0,168631

0,150798

0,049944

0,025298

10. Т. к. проверка на однородность дала положительный ответ, и результаты других оценок учтены, можем объединить  измеренные значения в одну серию.

Uвх,мВ	0	1	2	3	4	5	6	7	8	8,4
1	0,01	0,08	0,16	0,25	0,37	0,55	0,89	1,53	2,35	2,45
2	0,01	0,09	0,15	0,23	0,31	0,51	0,85	1,41	2,33	2,45
3	0,01	0,09	0,1	0,25	0,37	0,59	0,93	1,61	2,37	2,49
4	0,01	0,09	0,1	0,23	0,31	0,5	0,83	1,47	2,33	2,47
5	0,01	0,09	0,15	0,23	0,39	0,57	0,95	1,51	2,37	2,49
6	0,01	0,09	0,15	0,23	0,35	0,5	0,87	1,57	2,35	2,49
7	0,01	0,09	0,15	0,25	0,33	0,55	0,95	1,67	2,37	2,51
8	0,01	0,09	0,1	0,23	0,35	0,49	0,83	1,53	2,35	2,49
9	0,01	0,09	0,15	0,25	0,35	0,59	0,97	1,66	2,4	2,48
10	0,01	0,08	0,16	0,23	0,31	0,49	0,88	1,49	2,33	2,48
11	0,01	0,09	0,15	0,25	0,41	0,63	1,01	1,77	2,43	2,55
12	0,01	0,09	0,17	0,23	0,31	0,51	0,91	1,71	2,35	2,53
13	0,01	0,09	0,1	0,27	0,43	0,65	1,15	1,75	2,39	2,51
14	0,01	0,09	0,1	0,23	0,33	0,51	0,85	1,57	2,33	2,51
15	0,01	0,09	0,1	0,25	0,39	0,57	1,01	1,93	2,3	2,53
16	0,01	0,09	0,16	0,2	0,33	0,51	0,85	1,51	2,33	2,51
17	0,01	0,09	0,15	0,2	0,37	0,59	1,03	1,81	2,4	2,51
18	0,01	0,09	0,15	0,23	0,31	0,5	0,83	1,57	2,33	2,51
19	0,01	0,09	0,1	0,25	0,32	0,5	1,05	1,7	2,35	2,53
20	0,01	0,09	0,16	0,23	0,33	0,51	0,83	1,71	2,29	2,49

10.1 Определим средние значения объединенных таблиц как наиболее вероятные.

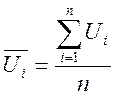
0,01

0,089

0,136

0,236

0,349

0,541

0,924

1,624

2,353

2,499

10.2 Определим случайные отклонения объединенных таблиц .