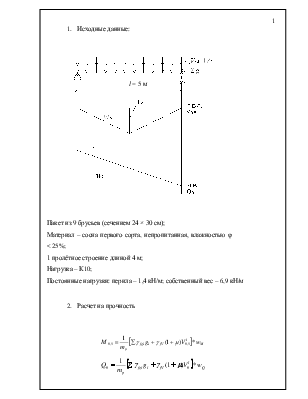





1. Исходные данные:
|
Пакет из 9 брусьев (сечением 24 × 30 см);
|
1 пролётное строение длиной 4 м;
Нагрузка – К10;
Постоянные нагрузки: перила – 1,4 кН/м; собственный вес – 6,9 кН/м
2. Расчет на прочность
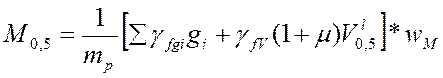
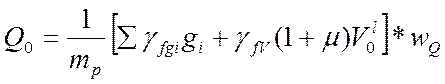
где mp = 2 – количество прогонов при езде на поперечинах;
![]() и
и ![]() –
площади линий влияния:
–
площади линий влияния:
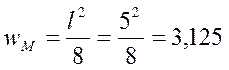 м2.
м2.
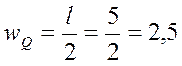 м2.
м2.
g1 – нагрузка от собственного веса:
![]() ,
,
где А = 0,072м2 – площадь поперечного сечения одного бруса; γ = 6 кН/м3 – объемный вес сосны;
![]() кН/м;
кН/м;
g2 – нагрузка от веса тротуаров с перилами (1,4 кН/м);
g3 – нагрузка от веса мостового полотна (6,9 кН/м);
γfgi – коэффициенты надежности для постоянных нагрузок (1,2);
γfv– коэффициент надежности для временной нагрузки:
![]() ;
;
(1+μ) = 1,1 – динамический коэффициент;
![]() и
и ![]() - временные эквивалентные нагрузки соответственно при α = 0,5 и α = 0 для
класса нагрузки К=10 (при длине загружения λ = l), принимаем по
таблице 1 приложения 5 СНиП 2.05.03-84:
- временные эквивалентные нагрузки соответственно при α = 0,5 и α = 0 для
класса нагрузки К=10 (при длине загружения λ = l), принимаем по
таблице 1 приложения 5 СНиП 2.05.03-84:
![]() ;
;
![]() ;
;
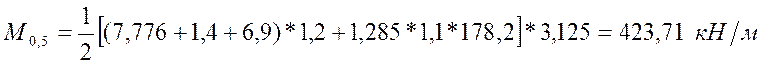 ;
;
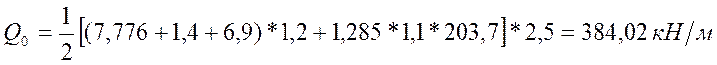 .
.
3. Проверка прочности
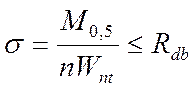 ;
;
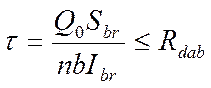 ,
,
где Wnt = 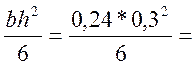 0,0036 м3 – момент
сопротивления поперечного сечения в середине пролета одного бруса нетто, т.е. с
учетом ослабления его отверстиями для болтов;
0,0036 м3 – момент
сопротивления поперечного сечения в середине пролета одного бруса нетто, т.е. с
учетом ослабления его отверстиями для болтов;
n = 9 – количество брусьев в одном прогоне;
Sbr = 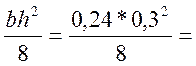 0,0027
м3 – статический момент части поперечного сечения бруса,
расположенной выше нейтральной оси относительно этой оси;
0,0027
м3 – статический момент части поперечного сечения бруса,
расположенной выше нейтральной оси относительно этой оси;
Ibr = 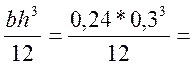 0,00054
м4 – момент инерции сечения в середине пролета одного бревна
относительно нейтральной оси;
0,00054
м4 – момент инерции сечения в середине пролета одного бревна
относительно нейтральной оси;
b = 0,24 м – ширина сечения бруса на уровне нейтральной оси; Rdb – расчетное сопротивление сосны на изгиб;
Rdab – расчетное сопротивление сосны на скалывание вдоль волокон при изгибе. Числовые значения расчетных сопротивлений принимаем по таблице 97 (СНиП 2.05.03-84) при влажности φ < 25%:
Rdb=15,7 МПа;
Rdab = 2,35 МПа;
 ;
;
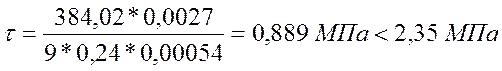 .
.
Проверка на прочность прошла успешно.
4. Расчет на смятие
Так как мы используем 1 пролёт длинной 5 метров, то давление на опору будет совпадать с величиной поперечной силы в этой опоре. В данном случае рассчитывается сопряжение прогона с насадкой, поэтому величина динамического коэффициента (1+μ) принимается равной 1,2.
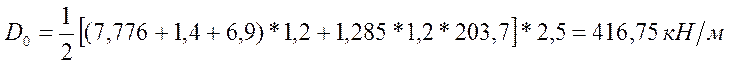 .
.
Проверка на смятие будет обеспечена при выполнении условия:
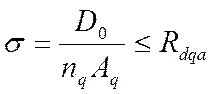
где nq = 3 – число площадок смятия; Aq – площадь одной площадки смятия:
![]() ,
,
где ls = 0,25 м – длина площадки смятия вдоль волокон древесины (ширина конуса).
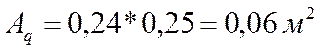 ;
;
Расчетное сопротивление Rdqa рассчитываем по формуле:
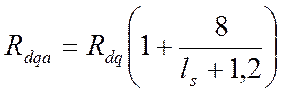
где Rdq = 1,77 МПа – расчетное сопротивление при смятии всей поверхности поперек волокон для древесины при влажности < 25%, принимаемое по таблице 97 СНиП 2.05.03-84:
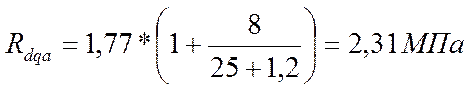
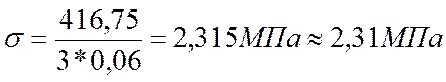
Проверка на смятие прошла успешно.
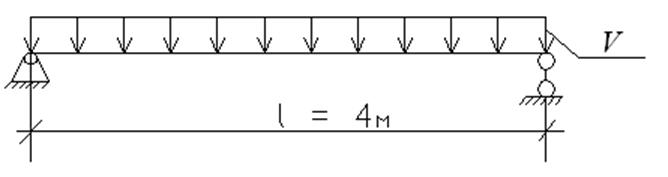
5. Расчет по предельному состоянию второй группы
|
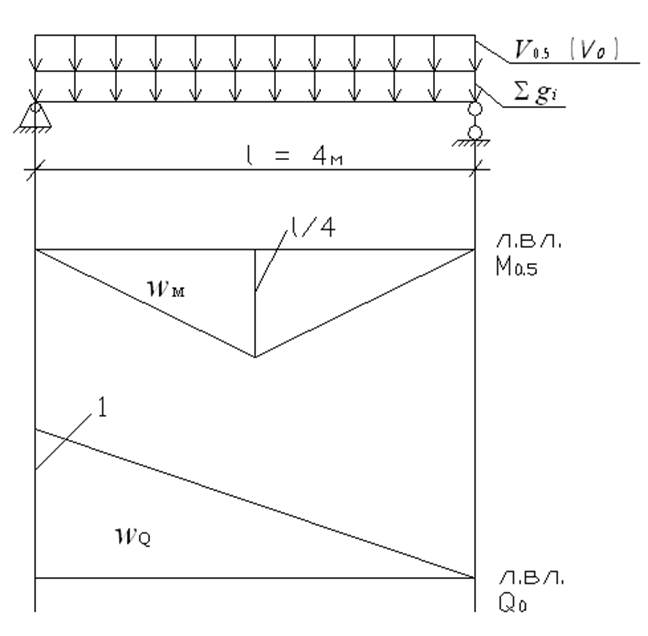
Прогоны должны быть рассчитаны по предельному состоянию второй группы на ограничение прогиба в середине пролета f0,5, который вычисляют по формуле:
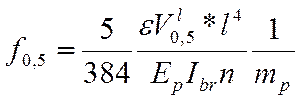 ;
;
где mp = 2 – количество прогонов при езде на поперечинах;
ε = 1 – коэффициент, учитывающий наличие в поездах только перспективных локомотивов и вагонов, а так же отсутствие тяжелых транспортеров;
Ibr = 0,00054 м4 – момент инерции сечения в середине пролета одного бруса относительно нейтральной оси;
Ер = 9810 Мпа – модуль упругости древесины при изгибе;
![]() = 178,2 кН/м – временная эквивалентная нагрузка при α
= 0,5 и длине загружения λ = l для класса нагрузки К=10 (принимаем по таблице 1
приложения 5 СНиП 2.05.03-84).
= 178,2 кН/м – временная эквивалентная нагрузка при α
= 0,5 и длине загружения λ = l для класса нагрузки К=10 (принимаем по таблице 1
приложения 5 СНиП 2.05.03-84).
Прогиб в середине балки не должен превышать предельного значения:
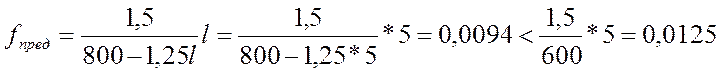 ;
;
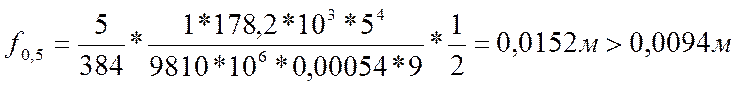 .
.
Полученный максимальный прогиб больше предельного, значит нужно изменить нашу конструкцию. Существует несколько вариантов решения данной задачи, сравним 2 наиболее подходящих и выберем наилучший.
1) Один из вариантов – увеличить количество брусьев в пакете. Чтобы определить необходимое количество брусьев в пакете для обеспечения прогиба, меньшего, чем предельный, выразим из формулы прогиба число брусьев n, а вместо искомого прогиба подставим предельный.
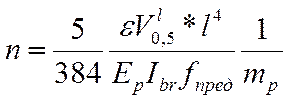 ;
;
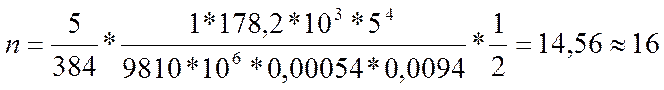 брусьев
брусьев
Таким образом, если решать задачу увеличением количества брусьев в пакете, нам понадобится 16 брусьев вместо заданных 9.
2) Ещё один способ – уменьшить длину пролётного строения моста. Для этого мы выразим из формулы прогиба длину пролёта, а вместо искомого прогиба также подставим предельное его значение.
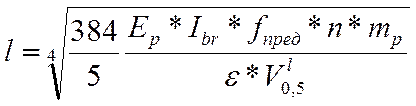 ;
;

Значит, если для решения задачи мы уменьшаем длину пролётного строения, примем пролёт длиной l = 4,4 м.
Теперь следует сравнить эти 2 варианты и выбрать наиболее рациональный. Исходя из того, что при увеличении количества брусьев в одном пакете с 9 до 16 штук мы будем использовать значительно больше древесины (в 1,7 раза), и конструкция станет заметно более материалоёмкой, остановимся на втором варианте решения данной задачи и примем длину пролётного строения l = 4,4 м.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.