![]()
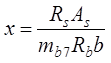 (2.9)
(2.9)
![]() -коэффициент условий работы, равный
0.9, учитывающий работу конструкции в северных районах [по п3.24, 1].
-коэффициент условий работы, равный
0.9, учитывающий работу конструкции в северных районах [по п3.24, 1]. ![]() ,
, ![]() -
расчетные сопротивления бетона и арматуры [по п3.24 и п3.37, 1] соответственно
для бетона класса B35 – 17,5 МПа, для арматуры класса АII – 250 МПа.
-
расчетные сопротивления бетона и арматуры [по п3.24 и п3.37, 1] соответственно
для бетона класса B35 – 17,5 МПа, для арматуры класса АII – 250 МПа.
На поперечную силу сечение рассчитывается по формуле:
![]() (2.10)
(2.10)
4) Расчет на выносливость.
При расчете изгибаемых элементов на выносливость принимается треугольная эпюра распределения напряжений (см. рис. 2.2), предполагается также, что бетон в растянутой зоне не работает, а растягивающие напряжения полностью воспринимаются арматурой. Исходя из этих предпосылок, получены следующие расчетные формулы:
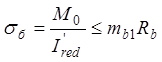
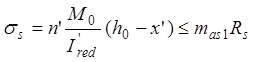 , (2.11)
, (2.11)
где ![]() и
и ![]() -
коэффициенты условий работы бетона и арматуры при расчете на выносливость,
принимаемые по п.3.26 и 3.39 [1], в зависимости от коэффициента асимметрии
цикла p = 0,123:
-
коэффициенты условий работы бетона и арматуры при расчете на выносливость,
принимаемые по п.3.26 и 3.39 [1], в зависимости от коэффициента асимметрии
цикла p = 0,123:
![]() ;
; ![]() (2.12)
(2.12)
где ![]() =1,28 – коэффициент, учитывающий рост
прочности
=1,28 – коэффициент, учитывающий рост
прочности
бетона (В35) во времени;
![]() = 1;
= 1; ![]() =1
– коэффициент, учитывающий сварные стыки арматурных стержней, выполненные
контактным способом с зачисткой;
=1
– коэффициент, учитывающий сварные стыки арматурных стержней, выполненные
контактным способом с зачисткой; ![]() =0,7.
=0,7.
n’ – условное отношение модулей упругости арматуры и бетона, принимаемое для B35 по п3.48 [1] равным 15.
x’ – высота сжатой зоны бетона, определяемая по формуле:
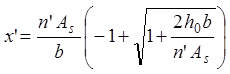 (2.13)
(2.13)
![]() - приведенный к бетону момент
инерции сечения:
- приведенный к бетону момент
инерции сечения:
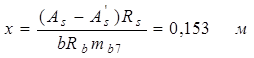 (2.14)
(2.14)
5) Расчет на трещиностойкость.
Плита балластного корыта рассчитывается по категории 3в требований по трещиностойкости в соответствии с п3.100 и п.п. 3.105, 3.109, 3.110.
По образованию продольных трещин в бетоне:
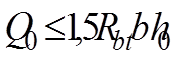 (2.15)
(2.15)
по раскрытию нормальных трещин:
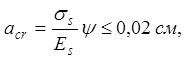 (2.16)
(2.16)
где ![]() - напряжение в арматуре,
определяемое по (2.11), но с заменой коэффициента n’ на
реальное соотношение модулей упругости стали арматуры АII
и бетона B35: n’=2,06/0,345=5,97;
- напряжение в арматуре,
определяемое по (2.11), но с заменой коэффициента n’ на
реальное соотношение модулей упругости стали арматуры АII
и бетона B35: n’=2,06/0,345=5,97;
![]() - коэффициент раскрытия трещин:
- коэффициент раскрытия трещин:
![]() , (2.17)
, (2.17)
где Rr-радиус армирования, определяемый по формуле:
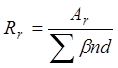 , (2.18)
, (2.18)
где Ar
– площадь зоны взаимодействия нормального сечения, принимаемая
ограниченной контуром и радиусом взаимодействия r=6d; ![]() - коэффициент сцепления
арматуры с бетоном (для одиночных стержней равен 1, [п.3.110, 1]); n – число
арматурных элементов с одинаковым номинальным диаметром (в данном случае равен
числу стержней); d – диаметр одного стержня.
- коэффициент сцепления
арматуры с бетоном (для одиночных стержней равен 1, [п.3.110, 1]); n – число
арматурных элементов с одинаковым номинальным диаметром (в данном случае равен
числу стержней); d – диаметр одного стержня.
Расчет по указанным выше формулам и проверки приведены в приложении 1 к данному курсовому проекту.
2.2 Расчет главных балок
Расчетная схема конструкции – неразрезная трехпролетная балка, выполненная по схеме 25-33-25 м. Материал – обычный железобетон. Класс бетона – B35, класс рабочей арматуры – АII.
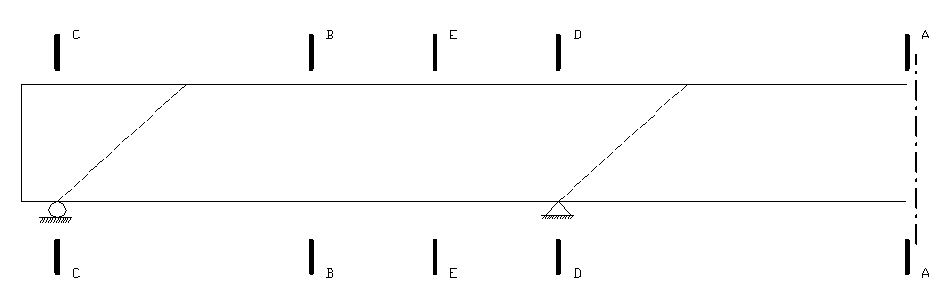
Рис.2.3. Расположение расчетных сечений главной балки
Расчет выполнен по предельным состояниям первой и второй группы и включает следующие проверки (см. рис. 2.3):
1) Сечения A-A:
· На прочность
· На выносливость
· На трещиностойкость
2) Сечения D-D:
· Прочность
· Трещиностойкость
3) Сечения В-В:
· Прочность
· Выносливость
· Трещиностойкость
4) Сечение Е-Е на выносливость
5) С-С на прочность по поперечной силе.
Пояснения к расчету изгибаемых элементов по предельным состояниям большей частью приведены в разделе 2.1 курсового проекта. Специфические для данной конструкции пункты пояснены в ходе расчетов ниже.
2.2.1. Линии влияния внутренних усилий.
Линии влияния моментов и поперечных сил в расчетных сечениях были построены с помощью программы Poluprom. Их вид и площади участков приведены в приложении 2 к данному курсовому проекту.
2.2.2. Определение расчетных усилий.
Все постоянные
нагрузки, кроме нагрузки от веса мостового полотна, введены в расчеты по
прочности с коэффициентами надежности ![]() .
К нагрузке от веса МП введен коэффициент
.
К нагрузке от веса МП введен коэффициент ![]() [1,
п.2.10]. Динамические коэффициенты
[1,
п.2.10]. Динамические коэффициенты ![]() для расчетов на
прочность и
для расчетов на
прочность и 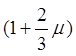 для расчетов на выносливость
определены в зависимости от длины загружения
для расчетов на выносливость
определены в зависимости от длины загружения ![]() и
и
![]() по формуле [п.2.22, б, 1]:
по формуле [п.2.22, б, 1]:
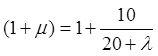 (2.19)
(2.19)
Таким образом, 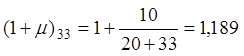 ,
,
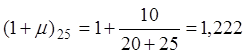
Коэффициенты ![]() , вводимые в расчеты на выносливость
и трещиностойкость, а также при определении прогибов, имеют следующие значения
[п.2.11, 1]:
, вводимые в расчеты на выносливость
и трещиностойкость, а также при определении прогибов, имеют следующие значения
[п.2.11, 1]: ![]() и
и ![]() .
.
Постоянные нагрузки введены в расчет со значениями:
·
От собственного веса ПС: ![]() (
(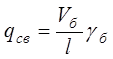 , где Vб=225,87
м3-объем железобетона балки, l=83 м – длина
ПС,
, где Vб=225,87
м3-объем железобетона балки, l=83 м – длина
ПС, ![]() =24,5 кН/м3 - объемный вес
ж.б.)
=24,5 кН/м3 - объемный вес
ж.б.)
·
От веса мостового полотна: ![]()
·
От веса перил: ![]()
·
От веса тротуаров: ![]()
Эквивалентные
нагрузки ![]() и
и ![]() определены
при
определены
при ![]() , независимо от положения вершины
линии влияния [п.2б, П5, 1]:
, независимо от положения вершины
линии влияния [п.2б, П5, 1]:
![]()
![]() .
.
Они
введены в расчет с коэффициентами надежности ![]()
![]() .
.
Ниже
приведены расчетные формулы внутренних усилий, где цифровые индексы при ![]() (площадях линий влияния) показывают
номер пролета, а
(площадях линий влияния) показывают
номер пролета, а ![]() без индекса означает
суммарную площадь линии влияния.
без индекса означает
суммарную площадь линии влияния.
1) Для расчетов на прочность:
· Сечение А-А:
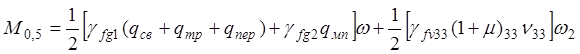
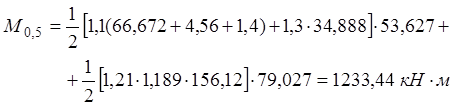
· Сечение D-D:
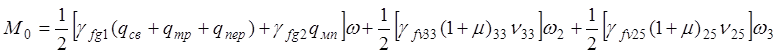
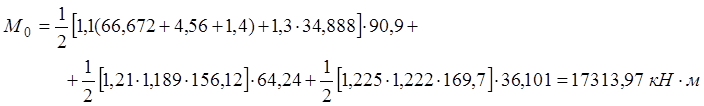
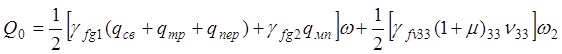

· Сечение B-B:
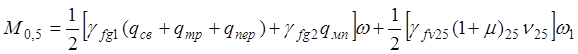
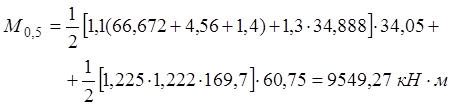
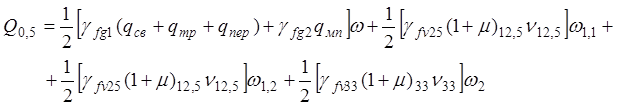
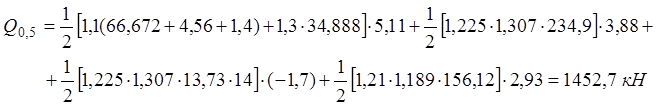
· Сечение С-С:
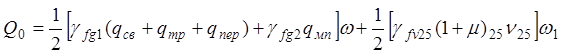
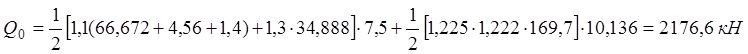
2) На выносливость:
·
Сечение А-А: 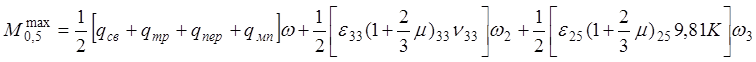
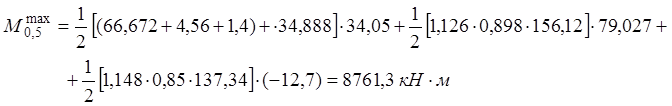
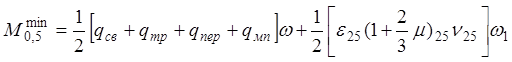
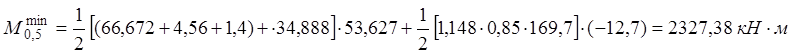
· Сечение В-В:
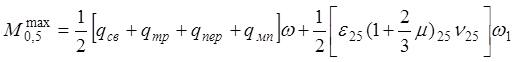

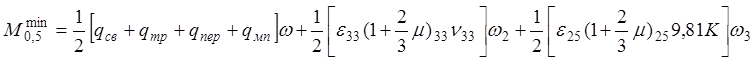
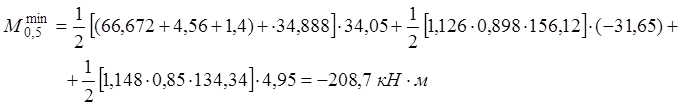
· Сечение E-E:
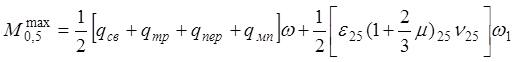
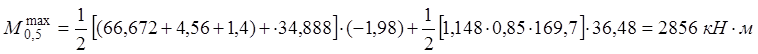
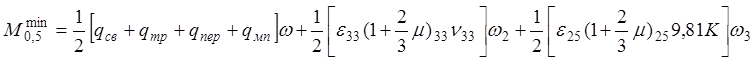
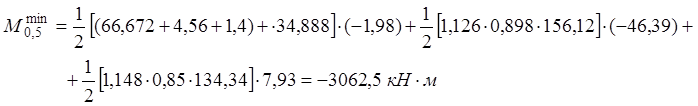
3) На трещиностойкость:
· Сечение А-А:
По образованию продольных трещин:
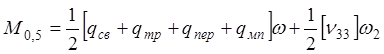
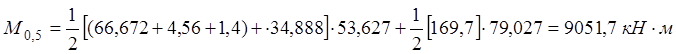
По раскрытию нормальных трещин:
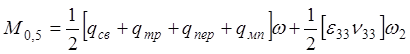
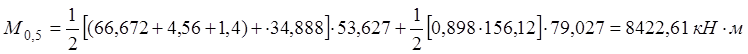
· Сечение В-В:
По образованию продольных трещин:
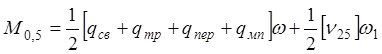
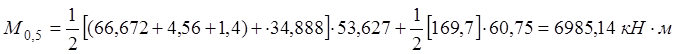
По раскрытию нормальных трещин:
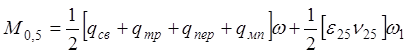

· Сечение D-D:
По образованию продольных трещин:

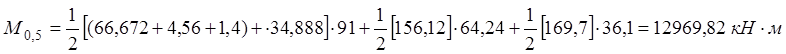 По раскрытию нормальных трещин:
По раскрытию нормальных трещин:
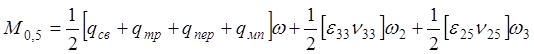
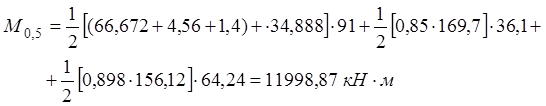
2.2.3. Расчетное сечение балки.
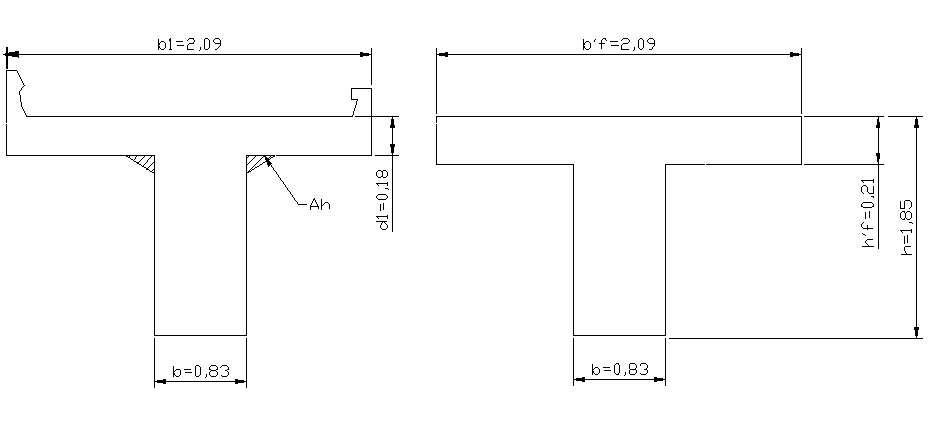
Рис.2.4. Действительное и расчетное сечения балки
При расчете главных балок допускается вместо действительного сечения использовать упрощенное расчетное (рис.2.4.), размеры которого определяются:
![]()
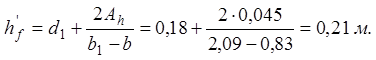
Полезная
высота сечения с учетом защитного слоя а=3 см предварительно принята: ![]() Соответственно, плечо внутренней
пары сил:
Соответственно, плечо внутренней
пары сил: 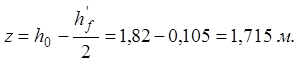
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.