Затем определяем величину lkk:
lkk = R(β - 2φ0). (2.13)
lkk = 600*(0,536 – 2*0,0417) = 271,56 м.
Для осуществления разбивки переходной кривой на местности по кубической параболе необходимо, чтобы выполнялось условие:
R ![]() 1,602С
1,602С![]() .
(2.14)
.
(2.14)
600 ![]() 1,602*30000
1,602*30000![]()
600![]() 492,
условие выполняется, принимаем кубическую параболу и координаты переходной кривой
определяем по уравнению:
492,
условие выполняется, принимаем кубическую параболу и координаты переходной кривой
определяем по уравнению:
yi
= ![]() . (2.15)
. (2.15)
Результаты расчетов отображены в таблице 2.3.
Таблица 2.3 Координаты переходной кривой по кубической параболе
|
X, м |
Y, м |
|
10 |
0,006 |
|
20 |
0,044 |
|
30 |
0,150 |
|
40 |
0,356 |
|
50 |
0,694 |
Расстояние m0 от тангенсного столбика (точка Т0 на рис. 2.4) бывшей круговой кривой до начала переходной кривой подсчитываем по формуле:
m0 = m+ρtg![]() , (2.16)
, (2.16)
где m ![]() 0,5*l0;
0,5*l0;
m0 = 25+0,174*tg30о45’/2= 25,05 м.
Полная длина новой кривой (с переходными кривыми) определяем по формуле:
Lkp = 2l0 + R(β - 2φ0), (2.17)
Lkp = 2*50 + 600(0,536 – 2*0,0417) = 371,56 м.
Суммированный тангенс новой кривой определяется по формуле:
Ткр = m + (R+ ρ)tg![]() ,
(2.18)
,
(2.18)
Ткр = 25 + (600+0,174)*0,275 = 190,05 м.
Суммированная биссектриса определяется по формуле:
Б0 = 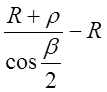 ,
(2.19)
,
(2.19)
Б0 = 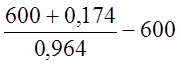 = 22,59 м.
= 22,59 м.
Домер определяется по формуле:
Д = 2Ткр - Lkp, (2.20)
Д = 2*190,05 – 371,56 = 8,45м.
Полученные параметры переходной кривой и элементы для ее разбивки характерны для всех четырех поворотов обходного пути. Разбивку переходных и круговых кривых на местности производят геодезическими способами.
2.3.4 Определение необходимой ширины рельсовой колеи в кривых
Ширина рельсовой колеи в кривых определяется из условий вписывания тележек подвижного состава, имеющих жесткую базу, в кривых соответствующего радиуса. Жесткая база L - это расстояние между крайними осями тележки или экипажа, остающимися при движении параллельными между собой.
Вписыванием подвижного состава в кривые называется установившееся при движении в кривой положение колесных пар жесткой базы относительно рабочих граней рельсовых нитей, возникающих в результате взаимодействия между рельсовым путем и ходовыми частями экипажа. В зависимости от длины жесткой базы, радиуса кривой и ширины колеи вписывание может быть свободным или принудительным и заклиненным.
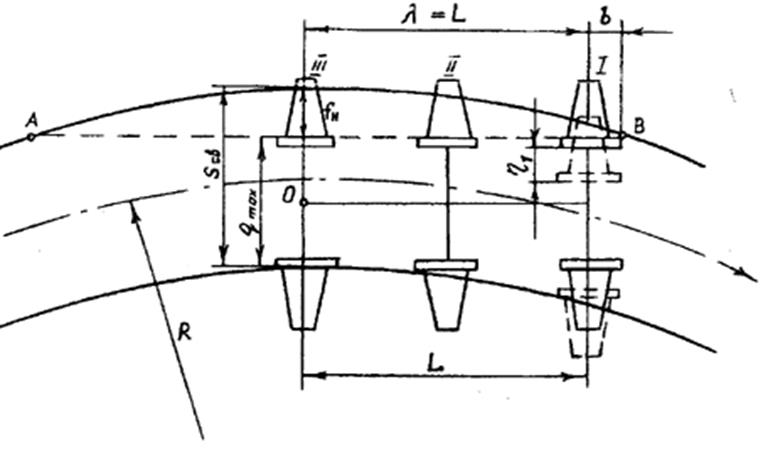 |
Рисунок 2.5 Схема свободного вписывания трехосного локомотива 2ТЭ10Л в кривую
Промежуточное положение жесткой базы тележки между заклиненным и свободным вписыванием характеризует принудительное вписывания, допускаемое в основном для локомотивов.
При свободном вписывании наблюдается минимальное силовое взаимодействие ходовых частей подвижного состава и колеи, а следовательно, наименьшие износы рельсов и колес и затраты энергии на движение. ( По этой причине стремятся обеспечить свободное вписывание).
При заклиненном вписывании колесные пары жесткой базы тележек не имеют никакой поперечной свободы, ввиду чего создаются особо не благоприятные условия взаимодействия подвижного состава и рельсовой колеи в кривой. В нормальных условиях эксплуатации оно не допускается.
Для облегчения вписывания тележек экипажей в кривые их колесные пары имеют, как правило, поперечные разбеги h относительно жесткой рамы.
На отечественных железных дорогах установлены следующие нормы ширины рельсовой колеи на кривых участках пути (таблица 2.6, /6/).
Таблица 2.3 – Нормативная ширина рельсовой колеи в кривых
|
Радиус, м |
Ширина колеи, |
|
R≥350 |
1520 (+8, -4) |
|
R=349…300 |
1530 (+8, -4) |
|
R≤299 |
1535 (+8, -4) |
Оптимальная ширина колеи определяется по формуле:
![]() , (2.21)
, (2.21)
где qmax – ширина колесной пары (таблица 2.1, /6/),мм;
fh – стрела изгиба наружного рельса, мм,
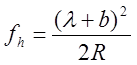 ; (2.22)
; (2.22)
λ – расстояние от центра тяжести вращения тележки О до оси первой колесной пары, при свободном вписывании λ=L;
L – длина жесткой базы (таблица 2.5, /6/), мм;
b – расстояние от оси первой колесной пары до точки касания гребня колеса с рельсом, мм.
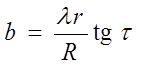 ,
(2.23)
,
(2.23)
где r – радиус колеса по среднему кругу катания, мм;
τ – угол наклона образующей гребня колеса к горизонту (для локомотивных колес τ=60˚);
η – разбег крайних осей (таблица 2.5, /6/), мм.
Для локомотива 2ТЭ10Л принимаем:
- qmax=1509 мм;
- длина жесткой базы L=λ=4200 мм;
- поперечные разбеги крайних осей η=1,5 мм;
- радиус колеса по кругу катания r=525мм;
- R=600000мм;
Расчет:
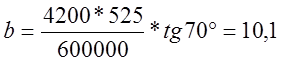 мм
мм
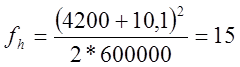 мм;
мм;
![]() мм
мм
Сравниваем Sопт и Sн=1520мм (таблица 2.6, /6/). 1527>1520, то есть Sопт>Sн, значит вписывание в кривую принудительное.
2.3.5 Определение числа укороченных рельсов по внутренней нити кривых
В кривой внутренняя рельсовая нить оказывается короче наружной на величину:
![]() ,
(2.24)
,
(2.24)
где β – центральный угол поворота, рад;
S1 – расстояние между осями рельсов,
S1=1600мм.
Получаем:
![]() мм.
мм.
Число укороченных рельсов на одном повороте определится по формуле:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.