Определение отношения теплоемкостей газов при постоянном объеме и постоянном давлении методом адиабатического расширения

                                                  Лабораторная работа №17

            Определение отношения теплоемкостей газов при постоянном объеме и    

                   постоянном давлении методом адиабатического расширения.

Приборы и принадлежности: Манометр, баллон, насос.

                                                             Введение

Теплоемкостью любого вещества, в том числе и идеального газа называется величина, равная количеству теплоты, которое необходимо сообщить, чтобы увеличить температуру вещества на 1⁰С. Если брать единицу массы, то соответствующая величина называется малярной теплоемкостью.

Между малярной теплоемкостью С и удельной теплоемкостью Сm  имеет место соотношение: С= m × с_m , где в системе СИ_m - масса 1 моля газа в кг (кг/моль).

При определении теплоемкостей газов необходимо различать, при каких условиях они нагреваются: при постоянном давлении или при постоянном объеме. Тогда получим соответственно молярную или удельную теплоемкость при постоянном давлении С_р или при постоянном объеме С_v. Их различие объясняется тем, что нагревание газа, при постоянном  объеме приводит только к увеличению его внутренней энергии, а нагревание газа при постоянном давлении связано с затратой тепла не только на увеличение внутренней энергии газа, но и на совершение работы по расширению газа.

Молярная теплоемкость при постоянном объеме выражается формулой:

                                         С_v=(i/2)R

где i - число степеней свободы молекулы газа (число независимых координат, характеризующих положение молекулы в пространстве), R - универсальная газовая постоянная, численно равная работе по нагреванию при постоянном давлении одного моля газа на один градус.

Молярная теплоемкость при постоянном давлении выражается формулой:

 С_р=С_v+R=[ (i+2)/2 ]×R. В данной работе мы будем находить отношение этих величин:¡=С_р /С_v . Подставив в эту формулу значения для С_р и С_v , получим: ¡=(i+2)/i. Таким образом, ¡ зависит только от числа степеней свободы молекул данного газа. Численное значение i зависит от числа атомов в молекуле. Для одноатомных молекул

i =3 , для двухатомных молекул i=5, для трехатомных молекул и многоатомных молекул i=6. В настоящей работе определяется ¡ для воздуха. Так, как воздух на 99% состоит из азота (N₂)  и кислорода (О₂), его можно считать двухатомным газом, т.е. i=5, ¡=1,4. Отношение теплоемкостей входит в уравнение Пуассона, описывающее адиабатический процесс РV¡=const.

Адиабатическим процессом называется процесс, происходящий без теплообмена с окружающей средой. Из уравнения 1-го начала термодинамики для адиабатического процесса (dQ=dА+dU, т.е. работа dА совершается только за счет внутренней энергии  dU газа. (dА= -dV).

Для определения g наиболее удобен метод, основанный на изучении адиабатического расширения газа.               

                           Описание аппаратуры и метод измерения

Прибор состоит из баллона Б и соединенного с ним манометра (рис.1). В баллон при помощи насоса накачивают воздух, создавая внутри баллона давление выше атмосферного. Это состояние воздуха будет соответствовать началу эксперимента. На графике (рис. 2) оно представлено точкой 1, которой соответствуют параметры газа Р₁, V₁ , Т₁. Любое быстрое расширение газа можно с достаточным приближением рассматривать как адиабатическое. Поэтому, если открыть кран А на короткое время и дать давлению внутри баллона сравняться с атмосферным, мы можем считать, что газ адиабатически перешел в новое состояние, характеризуемое величинами Р₂ ,V₂,  Т₂ (точка 2, рис. 2), где Р₂ - атмосферное давление. Температура газа (Т₂) после адиабатического расширения будет ниже окружающей (Т₁). Параметры начального и конечного состояния газа связаны уравнением адиабаты

                                         Р₁                                (1)

Через 3-5 минут газ нагревается до температуры окружающего воздуха (Т₁). Поскольку при этом нагревании V₂ неизменно, то давление повысится до Р₃. Новое состояние газа характеризуется новыми параметрами Р₃ , V₂ ,  Т₁ (точка 3 рис. 2). Сравнивая конечное состояние газа ( точка 3) с исходным (точка 1), видим, что они характеризуются одной и той же температурой. Тогда по закону Бойля- Мариота имеем:

                                         Р₃ V₂ =Р₁ V₁                                                       (2)

Возведем уравнение (2) в степень g и разделим его почленно на уравнение (1)

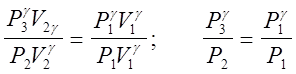                                            (3)

или                         .

Логарифмируя уравнение (3), находим g:

                                    g=In (Р₂/Р₁) In (Р₃/Р₁)                        (4)

Условие эксперимента позволяют упростить формулу (4) следующим образом: пусть Р₂ означает атмосферное давление (измеряется в см столба воды в манометре), а Н- разность уровней жидкостей в манометре до расширения, тогда

                                       Р₁=Р₂+Н                                         (5)

Разность уровней жидкостей в манометре после расширения обозначим через h, тогда

                                        Р₃=Р₂+h                                          (6)

 Поставив Р и Р в уравнение (4) будем иметь:

                               

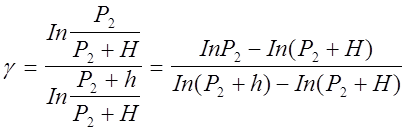
Так как давление Р₂ , (Р₂+Н) и (Р₂+h) незначительно отличаются друг от друга, можно для получения приближенного результата воспользоваться известной формулой математики In(1+x)=x  Iny » y-1. В таком случае

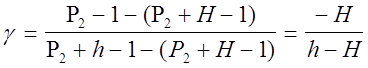                                   (7)

или окончательно     

                                        g=Н/(Н-h)                                     (8)

Эта формула является основной для определения g в данной работе.

                                          Порядок выполнения работы

1.  Составляют таблицу для записи результатов измерений.

1.

2.

...

5.

2.  Накачивают в баллон воздух так, чтобы разность уровней жидкости в манометре Н составляла 12 см.

3.  Закрывают кран и, выждав 2-5 мин.(до тех пор, пока уровни в трубках манометра перестанут изменяться), отсчитывают по шкале разность уровней жидкости в манометре- Н (отсчет вести по нижнему краю мениска).

4.  Открывают кран, и прислушиваясь к шипению выходящего воздуха, закрывают его сразу же по прекращении шипения, что соответствует выравниванию давления внутри баллона с атмосферным. Выждав 2-5 мин., отсчитывают по шкале разность уровней жидкости в манометре h. Результаты измерений заносят в таблицу. Опыт повторяют 5 раз. По формуле (8) вычисляют g для каждого измерения. Определить относительную и абсолютную погрешность результата:

                                

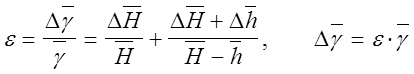
Тогда                         g = g ± Dg

                               Контрольные вопросы 1

1.  Какой процесс называется изохорическим и изотермическим?

2.  Какой процесс называется адиабатическим и каковы условия его осуществления?

3.  Почему при адиабатическом сжатии газ нагревается, а при расширении охлаждается?

4.  От чего зависит теплоемкость идеального газа?

                                   Контрольные вопросы 2

1.  Что называется числом степеней i свободы тела?

2.  Почему С_р >С_v ?

3.  Как зависят С_р и С_v от числа степеней свободы i молекул газа?

4.  Сколько и каких степеней свободы имеют газовые молекулы?

5.  Каков физический смысл универсальной газовой постоянной?

6.  Дайте определение 1 начала  термодинамики.

                                            Литература

1.  Зисман Г.А., Тодес О.М. Курс общей физики, т. 1,п. 45,46 1967.

2.  Грабовский Р.И. Курс физики, п.34, 1980

3.  Савельев И.В. Курс общей физики. Т. 1, п. 87-90, 1971.

4.  Трофимова Т.И. Курс физики, 1993.