МКЭ является численным методом, позволяющим получать приближенные решения разнообразных инженерных задач.
Обычно МКЭ используют в форме метода перемещений, когда узловые перемещения принимают за основные неизвестные.
Конструкция разбивается на конечное число элементов, тем самым снижается уровень задачи до конечного числа неизвестных.
Основные виды элементов конструкций на которые в расчетной схеме подразделяется целая конструкция:
Стержень-одномерная задача.
Пластина и оболочка – двухмерная задача.
Массивное тело – трехмерная задача.
Количество элементов на которые разбивается конструкция и массив грунта определяет точность расчета.
Элементы между собой соединены в узлах и имеют заданный закон распределения переменных (напряжений и перемещений) в пределах элемента, как правило в виде степенных полиномов. Степень полинома зависит от количества узлов в элементе.
Узловые значения перемещений становятся неизвестными, определив которые можно получить значение переменных в пределах всех элементов.
Принцип неразрывности системы основан на том факте, что в узле в котором соединяются несколько элементов, значение неизвестных одно и то же для всех элементов, сходящихся в этом узле.
Задача сводится к решению системы линейных или нелинейных алгебраических уравнений.
[ K ] { q } = { F }
[ K ] = ∑ [ кbi ] – матрица жесткости всей конструкции
{ q } – вектор искомых перемещений
{ F } – вектор внешних узловых сил.
Решение получают в виде узловых значений перемещений.
Выполняются дополнительные вычисления напряжений по найденным величинам перемещений.
На практике расчет сооружений МКЭ выполняется с помощью расчетных программ и сводится:
Подготовка исходных данных для расчета.
Расчет с использованием программного комплекса.
Интерпретация полученных результатов.
Для решения одномерных задач применяется программный комплекс Шапошникова TUN.
Для решения двух и трехмерных задач используются более современные програмные комплексы COSMOSM, PLAXIS, SOFISTICK.
Расчет сооружений МКЭ включает:
дискретизацию расчетной области, выбор интерполяционных функций, определение свойств элементов, сборку системы элементов, решение системы уравнений, дополнительные вычисления.
14. Предельные состояния конструкций. Пластические шарниры.
Предельным называется состояние конструкции, по достижении которого дальнейшая эксплуатация сооружения становится невозможной.
Строительные конструкции рассчитывают по 2 группам предельных состояний:
1) I группа - по несущей способности;
2) II группа - по деформациям и раскрытию трещин.
В расчет по несущей способности вводят расчетные нагрузки и расчетные сопротивления материалов.
Расчет по деформациям производят только на основные сочетания нагрузок, расчет ведут на нормативные нагрузки и нормативные сопротивления строительных материалов (для тоннельных обделок можно не производить!).
Расчетные нагрузки равны нормативным нагрузкам умноженным на коэффициент надежности по нагрузке.
Сечения бетонной обделки по мере увеличения в них внутренних усилий проходят следующие стадии:
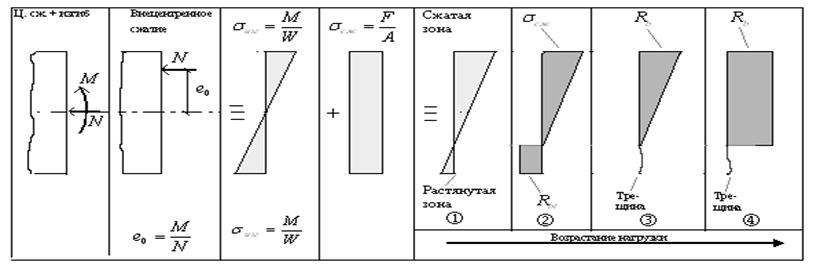

Итак:
стадия k предшествует образованию трещин в растянутой зоне
– это предельное состояние по недопущению трещин;
стадия m предшествует полному исчерпанию несущей способности
– это предельное состояние по несущей способности.
Эпюры нормальных сил(N) и изгибающих моментов(M). Опасные сечения
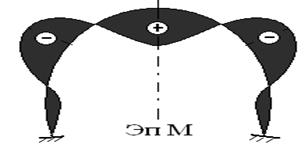
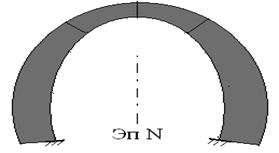
Опасные сечения: ![]()
обычно это замок и условные пяты свода. Опасное сечение может быть в обратном своде.
Пластический шарнир. Когда напряжения достигают значения предела текучести образуется пластический шарнир в статически определимой балке, превращает её в механизм, взаимный поворот которых относительно шарнира разрешит её.
Когда несущая способность исчерпывается повышаются пластические деформации в бетоне и текучесть арматуры. В наиболее нагруженном сечении пластические деформации арматуры достигнув предела текучести сохраняются постоянными.
15. Порядок проверки прочности бетонных конструкций в опасных сечениях.
Проверку прочности выполняют для каждого опасного сечения в следующем порядке:
1. Вычисляют эксцентриситет ![]() , где
, где 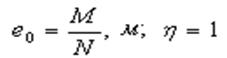
2. Если ![]() , всё сечение сжато (случай «малых
эксцентриситетов»). Проверку выполняют по формуле (1).
, всё сечение сжато (случай «малых
эксцентриситетов»). Проверку выполняют по формуле (1).
3. Если ![]() - при основном сочетании нагрузок или
- при основном сочетании нагрузок или ![]() - при
особом сочетании нагрузок проверяют дополнительно условия:
- при
особом сочетании нагрузок проверяют дополнительно условия: ![]() - для бетона
класса В >7,5
- для бетона
класса В >7,5
или ![]() - для других бетонов.
- для других бетонов.
Если оба условия по эксцентриситетам (основное и дополнительное ) выполняются, необходимо решить, до какой стадии можно допустить возрастание напряжений в сечении.
Когда грунты обводнены, а гибкая гидроизоляции отсутствует, образование трещин не допускается (стадия 2). В этом случае проверку выполняют по формуле (2).
В необводненных грунтах, или при наличии гибкой гидроизоляции, в растянутой зоне можно допустить ограниченное раскрытие трещин (до 0,2 мм) в растянутой зоне (стадия 4). В этом случае проверку прочности выполняют по формуле (3).
4. Если оба условия по эксцентриситетам, указанные в п. 3, - или хотя бы одно из них! – не выполняется, бетонная конструкция должна армироваться. В этом случае проверку прочности и подбор арматуры выполняют по формулам СНиП 2.03.01-84*, «Бетонные и ж.б. конструкции».
5. Когда проверка прочности не проходит, необходимо армировать конструкцию, либо увеличивать ее толщину, или класс бетона, или изменить очертание конструкции.
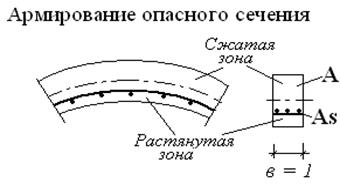
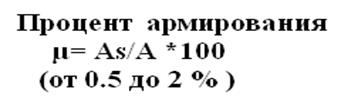
16. Формулы проверки прочности бетонных конструкций обделок при недопущении трещинообразования.
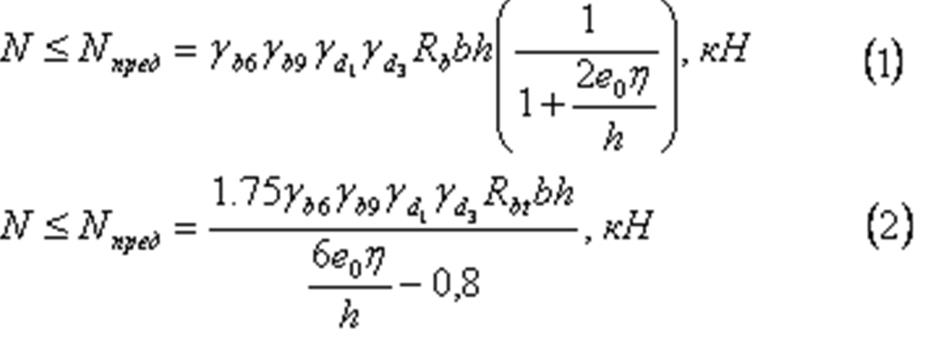
2. Если ![]() , всё сечение сжато (случай «малых
эксцентриситетов»). Проверку выполняют по формуле (1).
, всё сечение сжато (случай «малых
эксцентриситетов»). Проверку выполняют по формуле (1).
Когда грунты обводнены, а гибкая гидроизоляции отсутствует, образование трещин не допускается. В этом случае проверку выполняют по формуле (2).
17.Формула проверки прочности бетонной обделки при допущении ограниченного раскрытия трещин.
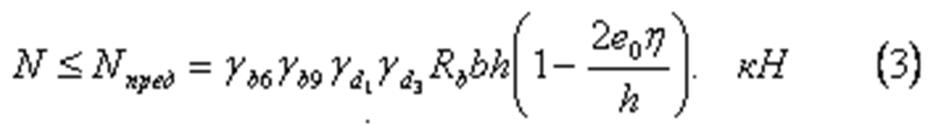
В необводненных грунтах, или при наличии гибкой гидроизоляции, в растянутой зоне можно допустить ограниченное раскрытие трещин (до 0,2 мм) в растянутой зоне. В этом случае проверку прочности выполняют по формуле (3).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.