При этом контур и прилегающие к нему слои в радиусе r = (3-5)d получают деформации (смещения), а напряжения в этих слоях перераспределяются.
Когда деформирующийся контур выработки вступает в контакт с крепью, последняя включается в работу и начинает препятствовать деформациям. С этого момента к гравитационным силам добавляется действие напряжений, возникающих на поверхностях контакта массива с крепью.
В дальнейшем приконтурный массив и крепь деформируются совместно до момента стабилизации деформаций.
Установившееся к этому моменту давление на контакте массива с крепью рассматривается как нагрузка от горного давления.
В такой постановке задачи горное давление определяется не только свойствами горного массива и геометрией выработок, но и совместными деформациями массива и крепи.
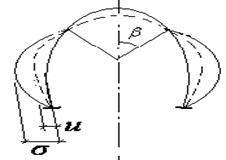
Взаимодействие грунтового массива и крепи: а) схема нагружения модели; б) диаграмма взаимодействия: 1 – график равновесных состояний; 2 - график сопротивления крепи; 3 – развитие смещении во времени.
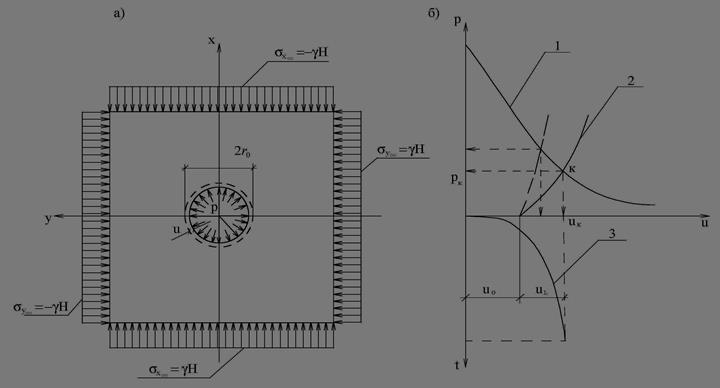
В реальных условиях крепь не сразу вступает в работу. К моменту ее установки контур получает смещение , а к моменту достижения равновесия – дополнительное смещение (кривая 2 на рис. б).
Этот момент изображен на рисунке
точкой k пересечения
кривых 1 и 2. Теперь крепь несет нагрузку, а контур получил смещение 
.
В случае применения более жесткой крепи (пунктирная линия на рис. б) нагрузка на крепь будет больше, а смещение – меньше, чем в предыдущем случае.
Таким образом, используя принципы взаимодействия массива и крепи, можно управлять горным давлением.
На этом и основаны положения новоавстрийского способа проходки: применение податливых крепей (набрызгбетон, анкера) и доведение деформаций почти до критической величины, благодаря чему максимально используется несущая способность приконтурных слоев массива, а крепь получается более экономичной.
11. Активные нагрузки и реакции грунта. Гипотезы общих и местных деформаций.
В специальной тоннельной литературе употребляют термины:
активные и реактивные нагрузки.
Теперь мы говорим:
нагрузки и
реакции опор конструкции.
Нагрузки и воздействия подразделяются
на постоянные и временные (длительные, кратковременные и особые).
К постоянным нагрузкам относятся:
1 -горное давление;
2 -гидростатическое давление;
3 -собственный вес конструкций;
4 -вес зданий и сооружений, находящихся в зоне их воздействия на обделку;
5 -сохраняющиеся усилия от предварительно обжатой обделки.
К кратковременным нагрузкам относятся:
-нагрузки от внутритоннельного и наземного транспорта;
-нагрузки от нагнетания раствора за обделку в процессе ее возведения;
-от усилий, возникающих при монтаже сборных обделок;
от веса и воздействия проходческого и другого стационарного оборудования.
К длительным нагрузкам и воздействиям относят:
-силы морозного пучения;
-вес стационарного оборудования;
-температурные климатические воздействия;
воздействия усадки и ползучести бетона.
К особым нагрузкам относят: сейсмические и взрывные воздействия.
Сочетания нагрузок:
- основные сочетания нагрузок (постоянные + длительные + кратковременные);
- особые сочетания нагрузок (постоянные + длительные + некоторые кратковременные + 1 особая).
Таким образом, если на сооружение действуют какие-то постоянные нагрузки и две особые, то расчет делают 3 раза (пояснить!).
Нагрузки вводят в расчет в наиболее неблагоприятных для конструкции сочетаниях.
а) Гипотеза общих деформаций: совместные деформации конструкции и окружающей среды под действием гравитационных сил
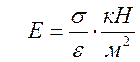В основе Теория упругости. (обобщенный модуль
упругости Ео , коэф-т попер. деф. (ню))
б) Гипотеза местных деформаций:
рассматривает деформации конструкции под действием активных сил и упругих
реакций (коэфф. постели):
 |
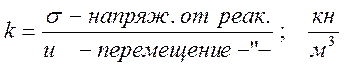12. Коэффициенты упругого отпора: удельный, за стенами и под фундаментом конструкции.
Взаимодействие обделки с окружающим грунтом может быть описано с помощью теории общих деформаций или теории местных деформаций. (см. лекцию 4).
Если среда рассматривается, как упругая (или пластичная, вязкоупругая и т.п.) и характеризуется модулем общей деформации и коэффициентом поперечной деформации , взаимодействия описываются формулами: (теория общих деформаций)
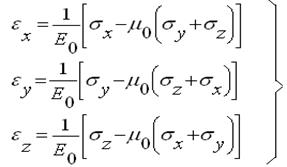
Проще использовать теорию местных деформаций (гипотезу Фусса-Винклера).
В
ее основе – прямая пропорцио-нальность между напряжениями и перемещениями на
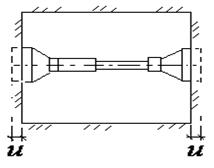
контуре: 
где
- коэффициент
упругого отпора грунта, 
.
(Аналог:
в теории общих
деформаций)
Главный недостаток метода местн. деф. – это то, что «
» зависит от
размеров площадок, контактирующих с грунтом, и это необходимо учитывать в
расчетах.
Определение коэффициентов упругого отпора
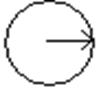
1) 
- удельный коэффициент отпора для выработки
одиночного радиуса ( 
)
или
полупролета выработки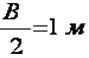 
;
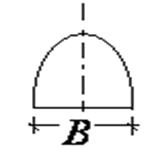2) с его помощью вычисляют коэффициент отпора за стенами обделки и под
обратным сводом:
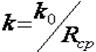или 
;
Где
-
средний радиус выработки, F – площадь поперечного сечения,м2; В
– пролет выработки, м.
3) под пятами разомкнутой обделки коэффициент отпора вычисляют по
формуле: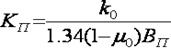 
, где ВП – ширина
пяты, м.
Связь между К и Е устанавливает
формула
Б.Г. Галеркина: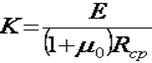 
Значения
в
зависимости от коэффициента крепости приведены в СНиПе «Туннели
гидротех-нические».
Для
сложных и дорогостоящих объектов 
определяют экспериментально.
Находят:
13.Расчетные схемы обделки по методу конечных элементов (программа МИИТа).
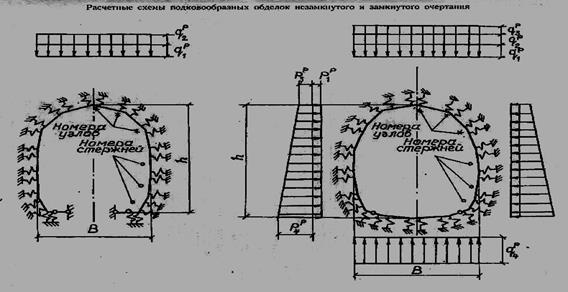Расчетной схемой называется условное изображение конструкции осевыми
линиями с указанием основных размеров, условий закрепления опор и нагрузок.
Расчетная схема устанавливается в зависимости от конструкции обделки, крепости грунтов, условий работы конструкций и способов ее возведения.
Метод расчета конструкции выбирают, исходя из ее схемы. До появления соврем. выч. техники на методы расчета накладывались ограничения в части объемов вычислительной работы, что вынуждало вводить в методику расчета упрощающие предпосылки и снижало точность результата.
Метод конечных элементов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.