Определение логарифмического декремента затухания колебательного движения

                                              Лабораторная работа №14

    Определение логарифмического декремента затухания колебательного

                                                        движения

Приборы и принадлежности: осциллограф, блок питания колебательного контура с переключателем сопротивлений.

                                   Методические указания

На практике все колеблющиеся тела находятся под воздействием различных сил, тормозящих движение (силы трения, сопротивления среды, наличие активного сопротивления в электрической цепи, содержащий колебательный контур и т.д.), поэтому амплитуда колебания постепенно уменьшается с течением времени. Простейшим механизмом убыли энергии колебания является превращение ее в теплоту вследствие трения в механических системах и омических потерь в электрических системах, при этом происходит постепенное затухание колебаний. Затухающие колебания- это такие колебания, амплитуда которых убывает со временем. Закон убывания амплитуд колебаний зависит от характера сил трения, действующих на тело. Уравнение затухающего колебательного движения имеет вид:

                                                                       (1)

                         где х- смещение относительно положения равновесия, А(t)=А₀ е^-Аt - переменная амплитуда колебания, b - постоянная величина, называемая коэффициентом затухания, w- угловая частота, t- время.

В условиях, где на колеблющееся тело действует квазиупругая сила F=КХ и сила трения F_тр-W, где r- коэффициент трения, V- скорость, уравнение движения для затухающих колебаний  согласно 2- го закона Ньютона будет иметь вид:

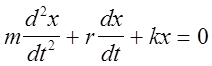                                                                                          (2)

Можно показать, что решением этого дифференциального уравнения 2- й степени будет уравнение (1).

На рис.2 показан график затухающего колебания для одного определенного типа сил трения. С возрастанием времени амплитуду убывает, асимптотически приближаясь к нулю. Чем больше коэффициент затухания, тем быстрее убывает амплитуда и сильнее затухание.

Более наглядной характеристикой затухания является логарифмический декремент затухания -d. Представляющий собой логарифм отношения двух амплитуд, соответствующих промежутку в один период, то есть:

                   

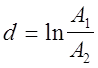
Амплитуды колебаний, отделенных во времени одним периодом, выражаются так:

                    A₁=A₀e^-bt ,           A₂=A₀e^-b(t+T)

Отношение этих амплитуд равно:

                   

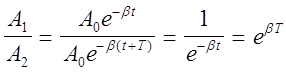
откуда

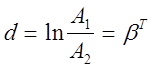                                                                    (3)

формулу (1) можно выразить через логарифмический декремент затухания, для этого из (3) найдем b и подставляя его значение в /1/, получим:

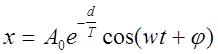                                                         (4)

                                        Описание установки

Можно сделать установку, которая будет состоять из тонкой стальной линейки L, тела B, заканчивающегося остием  для записи, вращающегося барабана l. Колебания линейки записываются на бумагу, прикрепленную на барабан С (рис.1)

рисунок

Если пустить в ход барабан, на котором укреплена бумага, сообщить колебательное движение линейке с телом, то это движение отобразится на бумаге временной разверткой колебаний в виде синусоиды (рис.2).

Пусть А₁- амплитуда первого колебания,

           А_n- амплитуда n -го колебания:

                      

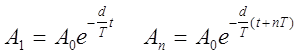
где n- число колебаний, их соотношение равно:

                     

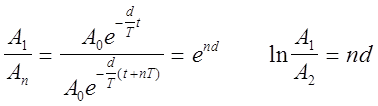
тогда:

                      

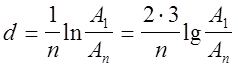
Между механическими колебаниями, характеризуемыми смещением Х, и электрическими колебаниями, характеризуемыми изменением заряда q или тока J во времени, существует полное подобие. Так, если взять колебательный контур, содержащий индуктивность L, емкость С, и активное сопротивление R, и подать в него какую-то разность потенциалов, то в данной цепи возникнут затухающие колебания. Так как часть энергии тратится на выделение тепла Джоуля- Ленца в сопротивлении R, то колебания будут затухать тем сильнее, чем больше R. Колебания тока (заряд и разряд конденсатора) происходят в следствии явления самоиндукции и будут описываться аналогичными уравнениями типа 1,2,3,4.

Если эти затухающие электрические колебания подать на соответствующие обкладки отклоняющих пластин осциллографа, то на его экране возникнет временная развертка q(t) аналогичная механическим затухающим колебаниям Х(t) (рис.2).

Так как электрические колебания q воспроизводятся надежнее и нагляднее, чем механические, то в качестве рабочей установки используется блок, содержащий колебательный контур с переключением для разных значений R т осциллограф.

                                        Порядок выполнения работы

1.  Включить питание колебательного контура и осциллографа в присутствии лаборанта. Так как один и тот же осциллограф используется в работе № 14 и 18, то при выполнении данной работы тумблер на столе должен быть включен в положение №14.

2.  Осуществить последовательное включение сопротивлений на блоке колебательного контура R₁  R₂  R₃.

3.  При этом на экране осциллографа будут изображены затухающие колебания для R₁, которые следует скопировать на кальку. Затем сделать то же самое для положения R₂ и R₃.

4.  Зависимость х(t) и А(t) на кальке изобразить разным цветом.

5.  Затем определить амплитуду 1-го и 5-го колебания для каждой из 3-х зависимостей.

6.  Вычислить логарифмический декремент затухания по формуле (5).

7.  Вычислить абсолютную и относительную погрешность однократного определения d.

                                                                                                               Таблица

А1	Аn	DА		d

                                                   Контрольные вопросы 1

1.  Почему большинство колебаний в окружающей нас природе являются затухающими?

2.  Каков порядок выполнения данной работы?

3.  Какие приборы используются в данной работе и от чего зависит погрешность определения логарифмического декремента затухания?

4.  Как связан логарифмический декремент затухания с коэффициентом затухания?

                                                    Контрольные вопросы 2

1.  Напишите уравнение движения для затухающих колебаний.

2.  Докажите, что выражение х=Аое^{- bt} cos(wt+у) является общим решением уравнения колебаний.

3.  От чего зависит амплитуда затухающих колебаний?

4.  Что общего между механическими и электрическими колебаниями?

5.  Как изменяется угловая частота затухающих колебаний?

                                                          Литература

1.  Зисман Г.А.курас общей физики. М. «Наука» ,1967г.,т.1,п.50,52,54.

2.  Грабовский Р.И., курс физики ,М. «Высшая школа», 1980 г.п.31.