Общие сведения о железобетонных мостах. Область их применения. Порядок проектирования мостов. Составление вариантов моста и выбор решения. Пролетное строение разрезной балочной системы. Мостовое полотно железнодорожных мостов, страница 4

d3  - полная  толщина балласта;  g3 =8кН/м; g 4=1,4кН.

Временную вертикальную нагрузку Uα от подвижного состава  определяем по  схеме СК  СНиП 2.05.03-84* приложение 5. При устройстве пути на балласте значения Uα≤19.62К кН/м, при λ≤25м следует принимать при α =0,5 независимо от положения вершины линий влияния. В эскизных расчетах усилия определяют в середине, в четверти и на опорном сечении, поэтому загружеамые площади линий влияния соответствуют  расчетным сечениям.

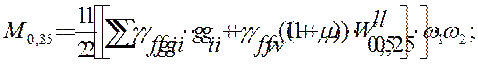Для расчетов по прочности:

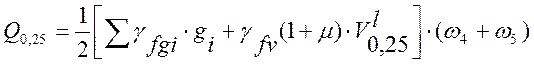
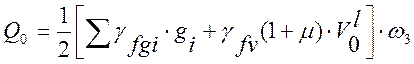
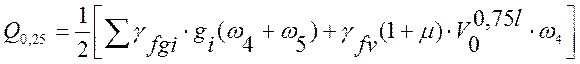
Для расчетов на выносливость.

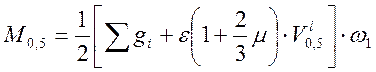
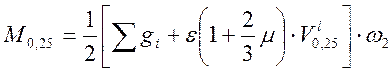
Для расчетов на трещиностойкость

По образованию продольных трещин

По раскрытию нормальных трещин

По ограничению касательных напряжений

По раскрытию наклонных трещин

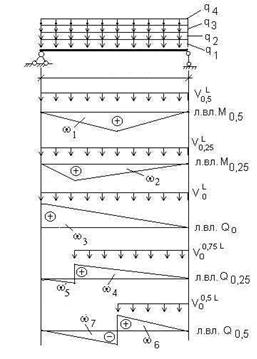
10. Расчет нормальных сечений главной балки на прочность:

Задача расчета состоит в обосновании формы и размеров поперечного сечения балок, площади арматуры и ее размещения в поперечном сечении. Обычно форму и основные размеры поперечного сечения балки – высоту балки, толщину и ширину плиты, толщину стенки – назначают на основе анализа проектов аналогичных конструкций. При этом ширина bf плиты, вводимая в расчет, должна удовлетворять условиям:

b_f≤12h_f+2c+b_c, b_f≤b₀

h_f – ширина плиты; c – ширина вута; b_c – толщина стенки; b₀ – расстояние в осях между соседними балками.

Расчет сечения в этих условиях сводится к проверке правильности принятых размеров и определению необходимой площади рабочей арматуры. Уточняются также размеры и формы пояса, в котором размещаются арматура, с учетом соблюдения расстояний между пучками, стержнями арматуры и размеров защитного слоя.

Необходимую площадь рабочей арматуры Ар предварительно определяют из условия, что расчетный изгибающий момент от внешних сил М будет воспринят парой сил на плече z.

М=R_pA_pz=R_pA_p(h₀-0,5h_f)

R_p – расчетное сопротивление арматуры; h₀ – рабочая высота балки; h_f – толщина плиты.

При этом предполагается, что толщина сжатой зоны x будет примерно равна толщине плиты h_f. Получаем:

A_p=M/(R_p/(h0-0,5h_f)).

По найденному значению Ар определяют необходимое число арматурных пучков или стержней и размещают их в нижнем поясе с соблюдением норм на размер защитного слоя бетона и на расстояния в свету между арматурными элементами. После этого проверяют подобранное сечение на прочность.

Условия прочности сечения по изгибающему моменту имеют вид:

Для случая когда х≤h’_f

M≤R_bb’_fx(h₀-0,5x)

x=R_sA_s/(R_bb’_f)

Для случая когда х≥h_f

M≤R_bbx(h₀-0,5x)+R_b(b’_f-b)h’_f(h₀-0,5h’_f)

x=(R_sA_s-(b’_f-b)h’_fR_b)/(bR_b)

Высота сжатой зоны ζ=x₀/h не должна превышать предельного значения ζy, при котором предельное состояние бетона сжатой зоны наступает не ранее достижения в растянутой арматуре напряжения, равного расчетному сопротивлению Rs или Rp.

Значение ζу определяют по формуле

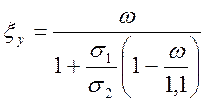
где ω=0,85-0,008R_b; σ₁=R_s – для ненапрягаемой арматуры, σ₂ – предельное напряжение в арматуре сжатой зоны, равное 500 МПа.

11. Расчет наклонных сечений главной балки.

Образование наклонных трещин при поперечном изгибе происходит в результате совместного действия изгибающего момента и поперечной силы. Обычно появляются нескольких наклонных трещин. Развитие их может начинаться от растянутой грани элемента, где трещины сначала проходят перпендикулярно растянутой арматуре, а затем, при дальнейшем развитии, направление трещин изменяется, они становятся наклонными, что связано с действием главных напряжений. Одна из трещин, называется «критической», получает наибольшее развитие. Такой трещиной элемент разделяется на два блока, связанных в жатой зоне бетона под наклонной трещиной, а в растянутой - продольной арматурой. Существует ещё одно усилие, способствующие соединению блоков - сила зацепления в наклонной трещине. Хомуты и отгибы пересекают трещину. При значительном влиянии поперечной силы, разрушение происходит в результате сдвига блоков относительно друг друга, а при доминирующем действии изгибающего момента - путем взаимного поворота блоков вокруг оси, проходящей через центр тяжести жатой зоны. Разрушение элемента по наклонному сечению обычно происходит в результате совместного действия поперечной силы и изгибающего момента.

Разрушение происходит:
1. в результате сдвига блоков;
2. путем взаимного поворота блоков вокруг оси, проходящей через центр сжатой зоны;
3. в результате раздробления бетона между наклонными трещинами.

Для железобетонных элементов с поперечной арматурой должно быть соблюдено условие, обеспечивающее прочность по сжатому бетону между наклонными трещинами ( т.е. будет исключаться разрушение):

В формуле:

Q - поперечная сила на расстоянии не ближе h0 от оси опоры;

- при расположении хомутов нормально к продольной оси

Где η=5 - при хомутах, нормальных к продольной оси элемента;

       η=10  то же, наклонных под углом 45⁰;

n1 -отношение модулей упругости арматуры и бетона.

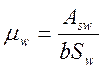
Asw - площадь сечения ветвей хомутов, расположенных в одной плоскости;

Sw - расстояние между хомутами по нормали к ним;

b - толщина стенки (ребра);

h0 - рабочая высота сечения.

Коэффициент φ_b1 определяется по формуле: φ_b1=1-0.01R_b

в которой расчетное сопротивление Rb принимается в МПа.

Q – максимальное значение поперечной силы от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения;

  - суммы проекций усилий всей пересекаемой ненапрягаемой (наклонной и нормальной к продольной оси элемента) арматуры при длине проекции сечения c, не превышающей 2h0;

       - угол наклона стержней (пучков) к продольной оси элемента в месте пересечения наклонного сечения;