Уравнение (4), формулы (1) и (5) являются исходными соотношениями свободных незатухающих гармонических колебаний. В зависимости от физической величины смещения Х(t) и возвращающей силы получается тот или иной конкретный вид колебаний.
В данной работе рассматривается простейший вид механических гармонических колебаний – колебания математического маятника.
Математическим маятником называется материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести.
Понятие математического маятника является абстрактным понятием - моделью реального колеблющегося на нити тела, размеры которого значительно меньше длины нити.
Рассмотрим уравнение
движения маятника (рис.2). На него действует сила тяжести mg и сила натяжения нити 
, результирующая которых и является
возвращающей силой FВОЗВР.:
(6)
Как следует из рис.2, 
= mg
sin j
и, так как при малых углах отклонения sin
j »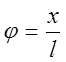
(где Х - смещение от
положения равновесия, l -
длина нити), тоуравнение (6) приобретает вид:
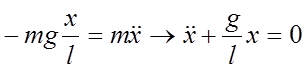(7)
 |
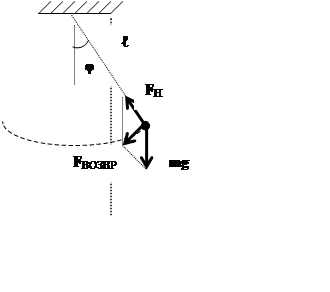Рисунок 2.
Знак (-) в первом из уравнений (7) указывает на то, что возвращающая сила направлена в сторону, противоположную смещению. Итак, как следует из уравнения (7), по сравнению с уравнением (4) и вытекающими из него формулами (1) и (5) при малых углах отклонения (малых амплитудах) движение математического маятника имеет характер гармонических колебаний вблизи положения равновесия
х =х0 sin (wt+α0),
с частотой и периодом, соответственно, равными
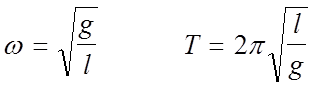(8) Формулы (8) позволяют определить ускорение свободного падения при известных характеристиках маятника ℓ, Т.
На практике для исключения ошибки, связанной с определением центра масс тела при измерении длины, измеряют разность длин. А именно, если Т1 - период колебаний маятника при длине ℓ1, а Т2 - при длине ℓ2 , то из формул для периодов колебаний
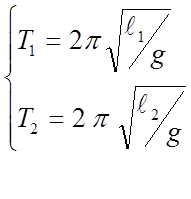
следует выражение для определения ускорения свободного падения по измеряемым величинам Т1 и Т2 и (ℓ1-ℓ2).
g =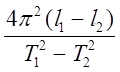
(9)
Маятник состоит из металлического шарика А (рис.3) диаметром 1,5 - 2 см, подвешенного на прочной нити длиной 1,5 - 2 м. Нить перекинута через блок В, укрепленный на стене или кронштейне, а второй конец ее закрепляется зажимным винтом С. Пользуясь блоком В, можно поднимать или опускать шарик и тем самым изменить длину маятника. Линейка со шкалой Д служит для измерения разности длин двух маятников.
1. Установить шарик маятника в нижней части шкалы и плотно приложить к ней сторону (катет) треугольника так, чтобы низ шарика касался другой стороны треугольника, тоже катета, как показано на рис.3. Отметить положение нижней точки шарика. Такой способ работы необходим для исключения ошибки на параллакс.
Рисунок 3.
2. Привести маятник в колебательное движение, но так, чтобы
угол отклонения был достаточно мал (не превышал 4...
)
. Определить при помощи секундомера время полных n колебаний и вычислить
период одного колебания по формуле
.
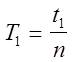Это измерение повторить три раза. Таким образом, будем иметь три значения для Т1. Найти их среднее значение, а по отклонению от последнего определить абсолютную погрешность DT1.
3. Поднять теперь шарик на 30-40 см; получается маятник с новой длиной. Определить период колебаний этого маятника тем же способом, что и в п. 2.
4. Заполнить таблицу измерений:
|
|
|
|
|
|
|
|
|
1 2 3 |
||||||
|
|
|
|
|
|
|
|
5. Рассчитать по формуле (9) среднее значение q в системе СИ.
6. Рассчитать по формулам (10), (11) относительную e (q) и абсолютную Dg погрешности:
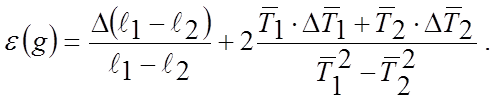(10)
(11)
1. Дайте определение гармонических колебаний, сформулируйте условия их существования.
2. Перечислите характеристики гармонических колебаний и дайте их определение.
3. Напишите уравнения смещения, скорости и ускорения при гармонических колебаниях и нарисуйте их графики.
4. Дайте определение математического маятника и напишите формулу его периода.
5. Объясните, чем вызвано ускорение, свободного падения и от чего оно зависит.
1. Зисман Г.А., Тодес О.М. Курс общей физики М. 1967. Т.1,п.58.
2. Грабовский Р.И. Курс общей физики М. 1980.п.29.
3. Савельев И.В. Курс общей физики М.1971.Т.1, п.66.
ЛАБОРАТОРНАЯ РАБОТА № 12
Определение коэффициента вязкости жидкости с помощью
закона Стокса
Цель работы: изучение внутреннего трения в жидкостях и определение коэффициента вязкости с помощью закона Стокса.
Приборы и принадлежности: сосуд с исследуемой жидкостью, таймер- секундомер, микрометр, миллиметровая линейка, шарики.
Введение.
Если в движущейся жидкости
или газе существует отличный от нуля градиент
скорости
DU/Dх в направлении
перпендикулярном движению (т.е. различные слои имеют разную скорость), то два
соседних слоя взаимодействуют друг с другом с силой внутреннего трения,
определяемой эмпирической формулой Ньютона
F=-h(DU/Dx)Ds, (1)
где Ds- площадь соприкосновения слоев, h - коэффициент пропорциональности в формуле (1) называется коэффициентом внутреннего трения или вязкости. Коэффициент вязкости является характеристикой среды и численно равен силе внутреннего трения, возникающей между двумя слоями единичной площади при градиенте скорости, равном единице.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
2
