Результат измерения даст интервал, в котором находится истинное значение измеряемой величины и чем меньше погрешность, тем уже данный интервал и наоборот.
Контрольные вопросы:
1. Что такое плотность, масса тела, вес тела?
2. В чем состоит физический смысл массы, плотности?
3. Какова единица измерения плотности массы?
4. Может ли использоваться плотность в анализе вещества?
Если да, то как? О чем говорит закон Архимеда?
5. Дайте определение массы и веса тела.
6. Что такое прямые и косвенные измерения?
7. Могут ли быть определены прямыми измерениями скорость, объём, масса?
8. Могут ли они быть определены косвенными измерениями? Ответы поясните.
9. В каких единицах измеряются абсолютная и относительная погрешности?
10. Какие погрешности называются случайными, систематическими?
Придумайте свои примеры источников этих ошибок.
11. Что такое цена деления? Как её определить?
12. Что такое приборная погрешность? Как её определить?
13. К каким погрешностям приведёт:
а) тряска стола с весами? б) постоянный наклон крышки стола?
в) недолив ртути в термометре? г) погнутая стрелка прибора?
14. Каковы правила округления абсолютной погрешности?
15. Каковы правила представления ответов?
16. Что означают приставки: деци (д), санти (с), милли (м), микро (мк), нано (н), пико (п), дека (да), гекто (г), кило (к), мега (М), гига (Г)?
17.
Утонет
или нет в воде сплошное тело без пустот, если оно изготовлено из вещества с
плотностью: а) 2.7 кг/дм. куб; б) 2,7 · 
кг/м.
куб; в) 2,7 · 
кг/м. куб; г) 2,7· кг/дм. куб; д) 2,7·
г/м. куб; е) 2,7·10 кг/мм. куб; ж)
2,7·
мг/мм. куб?
18.
Плотности
некоторых веществ приведены в таблице, из чего изготовлено тело, если плотность
этого вещества равна: 7,8· кг/м. куб; 7,6· г/см. куб; 0,78 кг/дм. куб; 2,7· кг/см. куб; 1,2 мг/мм. куб; 0,78· мг/м. куб; 7,8 кг/см. куб?
Ответ дайте только для тех веществ, которые приведены в таблице 3.
Таблица 3. Вещества и их плотности.
|
Вещество |
Плотность, кг/куб. м |
|
сталь (разные марки) |
(5,7 7,9) · |
|
Алюминий (разные марки) |
(2,5 2,9) · |
|
Дерево (разные породы) |
(0,4 1,0) ) · |
|
Эбонит |
1,2 ) · |
Лабораторная работа № 3
Определение момента инерции тела методом трифилярного подвеса.
Приборы и принадлежности: трифилярный подвес, секундомер, масштабная линейка, штангенциркуль, образцы для измерений.
Трифилярный (на трех нитях) подвес (см. рисунок 1) представляет собой круглую платформу, подвешенную на трех симметрично расположенных нитях, закрепленных у краев этой платформы. Наверху эти нити также симметрично прикреплены к диску меньшего диаметра. Платформа может совершать крутильные колебания вокруг вертикальной оси (ОО’), перпендикулярной ее плоскости и проходящей через ее середину; центр тяжести платформы при этом помещается на оси вращения. Период колебаний определяется величиной момента инерции платформы; он изменяется, если платформу нагружают каким- либо телом. Этим способом и пользуются в работе.
 |
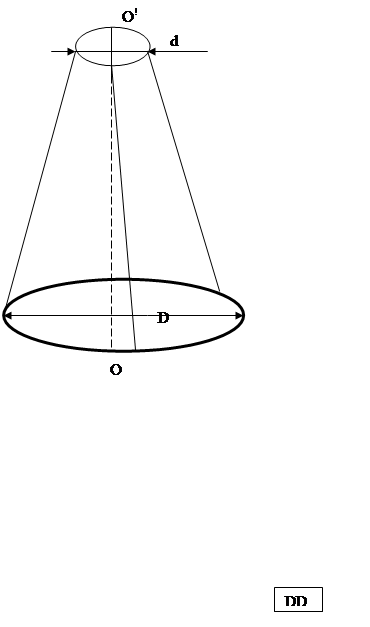Рисунок 1
Момент инерции тела I относительно оси вращения численно равен сумме произведений масс всех его точек на квадрат их расстояний до оси вращения
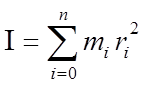
и является мерой инерции для вращательного движения. В настоящей работе момент инерции тела, центр тяжести которого совпадает с осью вращения трифилярного подвеса, можно найти как разность моментов инерции нагруженной и пустой платформ трифилярного подвеса.
Если ось вращения тела параллельна оси симметрии, проходящей через центр масс, но смещена от нее на расстояние а, то момент инерции относительно параллельно смещенной оси выражается соотношением, называемым законом Штейнера:
,
где 
-
момент инерции тела относительно оси симметрии, которая проходит через центр
масс тела. Центр масс или тяжести тела представляет собой точку приложения
равнодействующих элементарных сил тяжести.
,
где g– ускорение свободного
падения. Вращаясь затем в обратном направлении, платформа пройдет через
положение равновесия, и будет иметь в этот момент кинетическую энергию
,
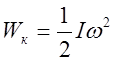где I-
момент инерции платформы; 
- угловая скорость
платформы в момент прохождения через положение равновесия.
Пренебрегая работой сил трения, на основании закона сохранения механической энергии можем написать:
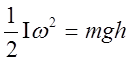(1)
Считая, что платформа совершает гармонические колебания, можем написать зависимость углового смещения платформы от времени t в виде
,
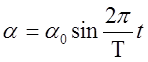где, α – угловое смещение платформы, α0 - амплитуда смещения, Т – период колебания. Угловая скорость ω, являющаяся первой производной α по времени, выразится так:
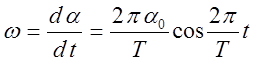
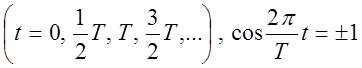
и абсолютное значение будет
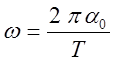(2)
mgh=
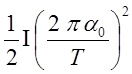(3)
При малых углах отклонения α высоту подъема h трифилярного подвеса можно выразить через его геометрические размеры (длину нити l, диаметры платформы D и верхнего диска d). Тогда из уравнения (3) можно получить рабочую формулу для определения момента инерции
.
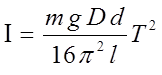(4)
По этой формуле может быть определен момент инерции как самой платформы, так и тела, положенного на все величины в правой части формулы могут быть непосредственно измерены.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.