Общая физика, механика: Методические указания к выполнению лабораторных работ по механике, страница 3

Вращательный импульс, необходимый для начала крутильных колебаний, сообщается платформе путем поворота верхнего диска вокруг оси при помощи рычага, связанного с диском. Этим достигается почти полное отсутствие других не крутильных колебаний, затрудняющих измерения.

По причинам, изложенным выше, амплитуда начальных колебаний не должна превышать 6-8⁰. Исследуемые тела надо положить на платформу строго симметрично, так чтобы не было перекоса платформы. Например, если тело имеет форму бруска, то его продольная ось должна строго совпадать с диаметром платформы.

Порядок выполнения работы.

1.  Трижды измерить величины l, D, d, (масса, m₀ платформы дается как постоянная прибора) и записать в табл. 1

                                                                                                Таблица 1

№ п/п

l1

l2

l3

lср

∆l

D

∆D

d

∆d

m0

m1

m

М

КГ

1

2

3

Среднее

2.  Сообщить платформе вращательный импульс и при помощи секундомера измерить время некоторого числа (30…50) полных колебаний. Указанные измерения проделать не менее трех раз и записать в табл.2.

                                                                                                       Таблица 2

№ п/п

∆Т

∆Т

I0

∆ I0

I1

∆ I1

I

∆ I

C

КГ• М2

1

2

3

Ср.

3.  Определить величину полного периода колебаний пустой платформы для каждой серии измерений и вычислить среднее значение периода Т₀.

4.  Вычислить момент инерции пустой платформы I₀ по формуле (4).

5.  Положить тело известной массы на платформу симметрично относительно ее центра. Определить период колебания всей системы (платформа + тело) Т.

6.  Вычислить момент инерции всей системы I₁ и записать в табл. 2.

7.  Величину момента инерции тела  определить как разность

                                                                                              (5)                                                              

8.  По формуле (4) подсчитать среднее значение моменты инерции         

пустой платформы I₀ и платформы, загруженной телом .

Определить относительную ε и абсолютную ∆I погрешности                     момента инерции Iтела и записать ответ в виде  .

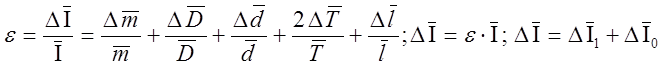
Контрольные вопросы I

1.  Что называется моментом инерции материальной точки тела относительно оси вращения?

2.  Какие колебания называются гармоническими?

3.  Как определяется кинетическая энергия вращающегося тела?

4.  Как записывается формула Штейнера?

  Контрольные вопросы II

1.  Дайте определение основных параметров, входящих в уравнение гармонических колебаний.

2.  Что называется моментом инерции тела и в чем его физический смысл.

3.  Дайте определение центра массы тела.

4.  Напишите закон сохранения энергии применительно к трифилярному подвесу.

Литература

1.  Зисман Г.А., Тодес О.М. Курс общей физики – М., 1967. Т.1, §10-11.

2.  Грабовский Р.И. Курс физики – М., 1980. §6,21,22.

3.  Савельев И.В. Курс общей физики. §38.

4.  Трофимова Т.И. Курс физики – М.,1993.

ЛАБОРАТОРНАЯ РАБОТА № 5

Определение ускорения свободного падения с помощью

математического маятника.

Цель работы: Изучение гармонических  колебаний и определение ускорения свободного падения на примере математического маятника.

Приборы и принадлежности: математический маятник, таймер- секундомер, линейка.

Введение

Гармоническим колебанием называется периодический по времени процесс, совершающийся по закону синуса или косинуса:

                        х(t)  = A sin j (t)= Asin [ wt+ j₀] ,                                (1)                                                              

где х(t) - колеблющаяся величина;  А=х_max – амплитуда (максимальное отклонение колеблющейся величины от положения равновесия); j(t) - фаза колебаний; j₀ - начальная фаза; w=2pT - круговая частота (число колебаний за 2p секунд); Т- период колебаний (время одного полного колебания).

Скорость и ускорение при гармонических колебаниях изменяются по следующим законам:

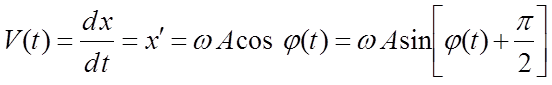           ,                                      (2)

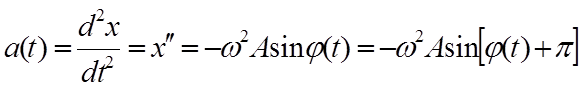             ,(3)

где V(t) - скорость, а(t)  - ускорение гармонических колебаний, которые как следует из формул (2) и (3), отстают по фазе соответственно на p2 и π от смещения x(t).

На рис. 1 представлены графики временных зависимостей смещения х(t) , скорости V(t) и ускорения а(t)  гармонических колебаний при φ₀ =0.

 

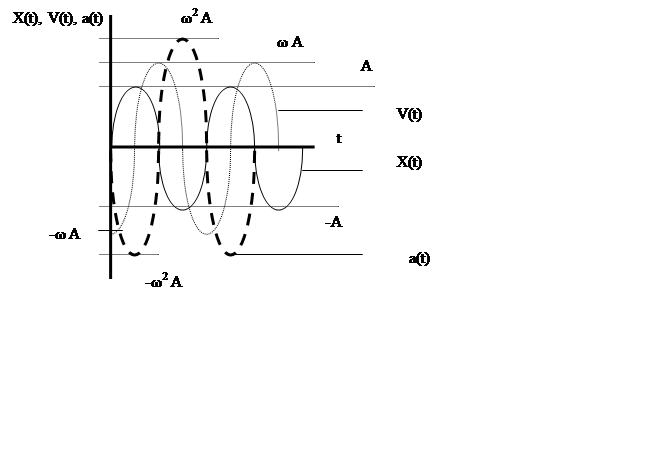Рисунок 1.

Причиной гармонических колебаний является действие на движущееся тело квазиупругой возвращающей силы типа: F= -kx. В этом случае основное уравнение динамики для движения вдоль оси Х записывается а виде:

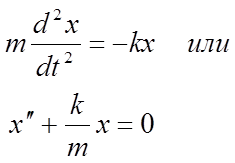                                                                                 (4)                                        

Уравнение (4) - дифференциальное уравнение свободных незатухающих колебаний, решением которого является выражение (1). Из (4) и (1) следует, что частота гармонических колебаний  зависит от массы тела и коэффициента квазиупругой силы:

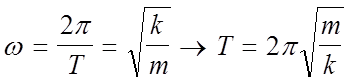                                                                    (5)