Изучение явлений, возникающих при деформации пружины

                                                Лабораторная работа №8.

         Изучение явлений, возникающих при деформации пружины.

Приборы и принадлежности: штатив с масштабной линейкой, упругая пружина с подвесом, набор разновесов, секундомер.

                                      Методические указания.

Под действием внешних сил Р всякое реальное тело деформируется, т.е. изменяет свои размеры и форму. Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называется упругой.

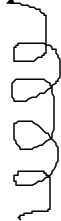
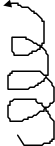
                                                                    Упругие деформации наблюдаются в том   

случае, если сила, обусловившая                           деформацию, не превосходит

 некоторый определенный для каждого                                                конкретного тела предел (предел упругости), когда D l / l₀ <<1. Простейшим видом деформации твердого тела является растяжение.

       Рис.1.

Оно возникает в пружине, один из концов которой закреплен, а к другому приложена внешняя сила F, стремящаяся ее растянуть (при противоположном направлении силы F возникает деформация сжатия). Заметим, что закрепление одного конца пружины, в силу 3-го закона Ньютона, равносильно приложению к закрепленному концу силы, равной по величине и противоположной по направлению силе, действующей на свободный конец. В состоянии равновесия внешняя сила F, например, сила тяжести груза подвешенного за свободный конец пружины, будет уравновешена упругими силами F_упр. Возникающими в пружине в результате деформации (см. рис.).

В 1660 году английский ученый  Р. Гук обнаружил, что при растяжении стержня или пружины длины l₀ и площади поперечного сечения S удлинение х прямо пропорционально внешней силе F, то есть х=1/к F, где k- коэффициент пропорциональности, который называется коэффициентом жесткости. Тогда закон Гука можно записать так      

                              F=kx                              (1)

Напряжение в стержне определяется величиной Q =F/S внешней растягивающей силы, отнесенной к единице площади S поперечного сечения. Упругие напряжения возникают по всей пружине и, очевидно, одинаковы вдоль всей ее длины. Это значит, что каждый элемент длины пружины действует со стороны прилегающих к нему частей пружины одни и те же усилия о . Ясно, поэтому, что каждая единица длины пружины подвергается одинаковому растяжению, так, что полное удлинение х = Dl  пружины будет пропорционально его общей длине.

При этом можно показать, что относительное удлинение l=Dl / l₀ прямо пропорционально приложенному напряжению  s, то есть

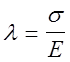
                                                          (2)

где Е - коэффициент пропорциональности, который носит название модуля или модуля Юнга.

Выражение (2), так же как и уравнение (1), соответствует закону Гука, оно наиболее часто используется в теории упругости, при рассмотрении сопротивления материалов, а в более общем виде, выраженном через соответствующий тензор, имеет более сложный вид, чем (2) или (1).

Упругие силы F_упр. например, возникающие в пружине при ее растяжении, прямо пропорциональны деформации (или смещению) х относительно положения равновесия пружины при отсутствии внешней силы, которое обычно связано с началом отсчета координаты х=0, и всегда направлены противоположно направлению смещения, к началу отсчета координат, то есть

                                               F_упр. =-kx               (3)

Под действием упругой или квазиупругой силы, не упругой по своей природе, но подчиняющейся выражению типа (3), тела после прекращения действия внешней силы, совершают гармонические колебания и подчиняются во времени закону косинуса и синуса. Поэтому упругие или квазиупругие силы называются так же гармоническими силами.

Движение под действием этих сил происходит в конечной области пространства и является финитным, при этом потенциальная энергия упругой деформации всегда меньше полной и минимальная. Когда колеблющееся тело находится в положении равновесия, то колебание тела на пружине под действием упругих сил можно описать с помощью 2-го закона Ньютона.

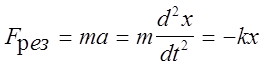                                      (4)

где m - масса колеблющегося тела. Уравнение (4) может быть записано в следующем виде

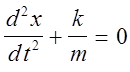                                                           (5)

при этом k/m>0.

Это дифференциальное уравнение второго порядка и имеет решение в виде следующей функции

                       x = x_maxcos(w₀l+j),                               (6)

где w₀- циклическая частота колебаний; j - начальная фаза в момент времени t = 0; w₀t + j - фаза колебаний в произвольный момент времени; х_max - максимальное смещение колеблющегося тела относительно положения равновесия.

Подставляя выражение (6) (положив j=0) в уравнение (5), убеждается, что (6) является решением последнего, когда

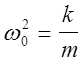                                                                   (7)

С другой стороны циклическая частота соответствующих колебаний определяется, как

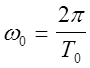                                                                 (8)

Где Т₀- период собственных колебаний- наименьший промежуток времени, за который все физические параметры, характеризующие колебательное движение, повторяются. Так, например по истечении Т₀ , фаза колебания получает приращение 2p, а колеблющееся тело возвращается в свое исходное состояние. Подставляя (8) и (7), находим, что 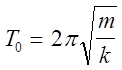                                             (9)

и период свободных упругих колебаний тела массой т, подвешенного на пружине, зависит от его массы и коэффициента упругости или жесткости пружины. Отметим, что для всех простых гармонических движений период колебания не зависит от амплитуды колебаний х_max до тех пор, пока выполняется закон Гука. При превышении этого предела тело получает остаточные или пластические деформации. Пластическими деформациями называются такие деформации, которые сохраняются и после прекращения действия внешней силы.

Упругие свойства пружины широко применяются на производстве, в измерительных приборах, в механических весах, игрушках ит.д. Упругие свойства пружин зависят от температуры, меняются со временем, что ограничивает их применение в измерительной технике, что понижает точность, например, в простых пружинных весах.

                                Описание установки.

В установке, которую условно назовем пружинным маятником, используется упругая пружина, один конец которой закреплен, а другой вместе с подвешенной к пружине площадкой для грузов, может двигаться относительно линейки. Конец которой совпадает с указателем на пружине при отсутствии внешней силы, а при нагружении- подвес указателя показывает удлинение пружины. Если пружину с подвесом оттянуть, а затем отпустить, то под действием упругих сил она будет совершать вертикальные колебания. Время, затраченное на n полных колебаний, можно определить по секундомеру. Под одним полным колебанием подразумевается наименьшее время, за которое колеблющееся тело вернется в исходное состояние, т.е. время, близкое к периоду колебаний.

                  Порядок выполнения работы и обработка

                                результатов измерений.

1.  Отметить пол шкале линейки положение указателя на пружине ненагруженного подвеса х₀, которое, как правило, совпадает с началом отсчета на измерительной линеке.

2.  Постепенно нагружая подвес разновесками с массами от m₁=50г, m_n=300г, определить соответствующее удлинение пружины Dх_i  =х_i-х₀ .

3.  Результаты отсчетов  по пп. 1-2 занести в табл. 1 и туда же вписать результаты расчетов внешней силы F_i = mg.

  4. Построить график зависимости смещения (удлинения пружины) от     действующей силы (F_i =m_i g) D x_i =f(F_i) и по графику определить коэффициент       жесткости пружины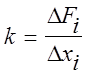                                                                                                                      

                                                                                                                            Таблица 1.

№ п/п	mi кг×10-3	Fi=miqH	Dx м
1 2 - - -	50 100 - - 300

                                                                                                                             Таблица2.

№ п/п	Тi c	n
1 2 3

      6.Поместив на подвес гирьку массой 50 г. , оттянуть подвес на 4 см. и, опустив     его, определить время 30 полных колебаний с тем, чтобы вычислить период     колебаний пружинного маятника по формуле Т=1/n (n=30). Сравнить полученное со значением периода, вычисленным по формуле (9), в   которой m=m₀+m₁ - масса подвеса с пружиной m₀=100 г., m₁=50г. -масса груза, при котором находится период Т; К- коэффициент жесткости, согласно п.4.

   6. Рассчитать среднюю квадратическую погрешность  и границы доверительного интервала абсолютной погрешности   

;

n- число измерений; t_a(n)- коэффициент Стьюдента. Для n=3,  t_a(n)=4,3;   n=5, 

t_a(n)=2,8.

    7. Результат определения периода представить в виде с.

                             Контрольные вопросы I.

1.  В чем состоит цель данной работы и с помощью каких приборов она реализуется?

2.  Какие виды деформации вы знаете?

3.  О чем говорит закон Гука?

4.  Какие силы называют упругими, квазиупругими?

5.  Дайте определение периода колебаний.

                                        Контрольные вопросы II.

1.  Какие условия являются необходимыми и достаточными для осуществления финитного движения?

2.  Какие колебания являются гармоническими  и зависят ли они от амплитуды колебаний?

3.  На основе уравнения движения тела, колеблющегося на пружине, выведите выражение для собственных колебаний.

4.  Нарисуйте и объясните особенности графика, показывающего зависимость относительного удлинения тела от напряжения при упругих и пластических деформациях.

                                                Литература.

1.  Зисман Г.А. Тодес О.И. Курс общей физики, М. 1967. Т.1, п.51.

2.  Савельев И.В. Курс общей физики. М. Т.1,п.14.

3.  Грабовский Р.И. Курс общей физики. М. 1980 п.10.