Лабораторная работа №19
Исследование механического резонанса
Приборы и принадлежности: закрепленный стальной стержень, звуковой генератор, частотомер- хронометр, осциллограф, электромагнит, катушка индуктивности.
Методические указания
Колебательные движения широко распространены в природе и технике. Это колебания уровня моря при отливах и приливах, биение сердца человека, вибрация струны в гитаре, переменный ток, колебания математических маятников, колебания атомов и молекул вещества и т.д.
В теории колебаний и волн колебания различной физической природы рассматриваются с единой точки зрения, С помощью разложения в ряд фурье любой колебательный процесс можно представить в виде совокупности простейших периодических колебаний, называемых гармоническими.
Периодические изменения гармонической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются гармоническими колебаниями. Их уравнение х=х0 sin(wD t+a), где через Х обозначается какой- либо физический параметр, характеризующий колебательный процесс- смещение, сила переменного тока, переменное напряжение, напряженность электрического и магнитного полей, отклонение атома или молекулы в веществе от положения равновесия.
В случае механических колебаний Х-
смещение материальной точки или тела от положения равновесия в любой момент
времени t. Х0- амплитуду колебаний- максимальное
смещение точки от положения равновесия, 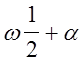 -
фаза колебания, a- начальная фаза, w0 -
циклическая или круговая частота, w0=2pV0, где V0-
частота колебания- число колебаний в единицу времени.
-
фаза колебания, a- начальная фаза, w0 -
циклическая или круговая частота, w0=2pV0, где V0-
частота колебания- число колебаний в единицу времени.
Для осуществления колебаний необходимо выполнить 2 условия:
1. тело должно иметь положение устойчивого равновесия,
2. при отклонении тела от положения равновесия, должна возникать упругая или квазиупругая сила, возвращающая тело в положение равновесия.
Под действием упругой, квазиупругой
силы тело начинает двигаться (колебаться) с ускорением, значит, -кх=ma
(по закону Ньютона), 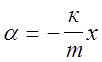 .
.
Обозначим к/m=w20 . Учитывая, что 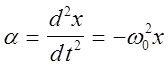 ,
получим дифференциальное уравнение
гармонических колебаний. Его решением будет уже упоминавшееся выражение х=х sin
(w0 t+a) или
,
получим дифференциальное уравнение
гармонических колебаний. Его решением будет уже упоминавшееся выражение х=х sin
(w0 t+a) или
х=х cos (w0 t+a).
В реальных условиях на тело, выведенное из положения равновесия и начавшее колебаться, действует сила сопротивления среды, поэтому колебания тела являются затухающими. Fсопр=-vr, где v- скорость тела, r- коэффициент сопротивления.
Для создания незатухающих колебаний необходимо восполнять потери энергии колеблющегося тела из-за сопротивления с помощью внешней периодической силы. Колебания, происходящие под действием внешней периодической силы, называют вынужденными.
-кх - vr +F = ma, F- внешняя вынужденная сила. Введем обозначения
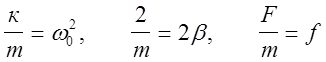 .
.
Тогда получим дифференциальное уравнение вынужденных колебаний
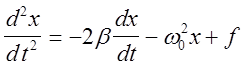 .
.
Пусть на тело, способное совершать собственные колебания с частотой V0 , действует внешняя сила, изменяющаяся по гармоническому закону f=f st wt=F sin2p wt, где F- амплитудное значение силы, V -ее частота. При совпадении частоты внешней вынужденной силы с частотой собственных колебаний тела, наблюдается явление резонанса- резкое возрастание амплитуды колебаний тела. Амплитуда вынужденных колебаний тела будет иметь максимум при частоте вынуждающей силы:
![]()
Если сопротивление среды отсутствует, то wрез=w0 и амплитуда вынужденных колебаний становится бесконечно большой. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приведенной на рис. 1, для реальных условий, т.е. для случая b¹0.
Из рис.1 видно, что чем больше коэффициент затухания b тем менее остро выражен максимум амплитуды.
Резонанс наблюдается при колебаниях любой природы ( механических, звуковых, электрических). Он широко применяется для усиления звука, приема и передачи электромагнитных колебаний в радиотехнике.
В данной работе резонанс исследуется на приеме механических колебаний стального стержня длиной l и диаметром D, закрепленного на концах.
Такой стержень (или струна) может колебаться с различными собственными частотами, при этом на длине стержня может укладываться различное число полуволн.
Теоретический анализ показывает, что характер колебаний стержня определяется его механическими и инерционными свойствами. Для круглого стержня, шарнирно закрепленного на концах
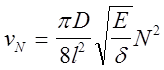 ,
где VN - частота собственных колебаний стержня,
,
где VN - частота собственных колебаний стержня,
p-3,14, D- диаметр стержня, М, l- длина стержня, М, Е- модуль упругости, модуль Юнга, ![]() , d- плотность
стали,
, d- плотность
стали,![]()
![]() ,
N=1,2,3,....
,
N=1,2,3,....
Описание метода измерения установки
Для получения свободных колебаний стержня необходимо вывести его из равновесия и предоставить его самому себе. Возникшие свободные колебания быстро затухают. Чтобы сделать эти колебания незатухающими приложим вынужденную силу в некоторой точке стержня (рис.6).
По обмотке электромагнита (1), расположенного против центра стержня, пропускают переменный ток частоты V от генератора 3Г. Этот ток создает магнитное поле такой же частоты. В результате на стальной стержень действует поперечная сила, изменяющаяся по гармоническому закону с частотой V. Эта сила вызывает поперечные колебания стержня.
Установим около стержня катушку 1 (рис.6). Колебания стержня индуцируют переменное напряжение, изменяющееся по гармоническому закону, во 2 катушке. 2-я катушка играет роль индикатора, регистрирующего поперечные механические колебания стержня. Сигнал с катушки 2 подается на регистрирующий осциллограф.
Блок схема- установки.
Порядок выполнения работы
1. Включить в сеть звуковой генератор 3Г, частотомер Ф-5034 и осциллограф С-1-49. Подождать 5 мин. На осциллографе- прямая линия, частотомер показывает 0 и mv звукового генератора 0.
2. Вращая ручку «сеть» 3Г вправо, подать на выход 3Г-1в, при этом стрелка mv переместится на всю шкалу до красной отметки.
3. Плавно вращая ручку «точно» 3Г, добавить на осциллографе максимального сигнала. Записать частоту которую показывает ф5034 как vрез. Повторить измерения 3 раза.
|
n |
vрез |
Dv рез |
4. Снять резонансную кривую. Для этого вращая ручку «точно» 3Г и увеличивая частоту через 1Гц, записывать размер сигнала на осциллографе, пока на экране не появится прямая линия.
Данные занести в таблицу.
|
V Гу |
|
|
Uосц дел |
|
|
Uосц |
|
|
|
|
|
отн.ед. |
Вернуться к Vрез , т.е. добиться опять максимального сигнала на экране. Вращая
ручку «точно 3Г, уменьшить частоту через 1 Гц и записывать размер сигнала на
осциллографе (опять до появления прямой линии на экране). Данные занести в
таблицу Примечание: этот пункт выполнить медленно.
5. По данным таблицы и Vрез построить резонансную кривую на миллиметровке
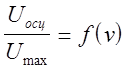
В отчете представить ![]() , резонансную кривую и расчет Ест,
Модуль Юнга стали Ест находим так: Ест=kq Vрез , где d=7,8 ×103×
, резонансную кривую и расчет Ест,
Модуль Юнга стали Ест находим так: Ест=kq Vрез , где d=7,8 ×103×![]() ,
,
К- коэффициент для данной установки.
Контрольные вопросы 1
1. Цель работы.
2. Каким методом исследуется резонанс в данной работе?
3. Что можно найти, исследуя резонанс колебаний металлического стержня?
4. Дать определение гармонических, затухающих, вынужденных колебаний.
5. Объяснить блок- схему установки.
Контрольные вопросы 2
1. Необходимое и достаточное условие гармонических колебаний.
2. Напишите дифференциальное уравнение вынужденных колебаний.
3. Резонансная кривая. От чего зависит пик амплитуды при резонансе? Условия наблюдения резонанса.
4. Объяснить полученную резонансную кривую.
Литература
1. Фриш С.Э., Тиморева А.В. Курс общей физики, 1962 г. т.1.,п. 2, 97, 98.
2. Грабовский Р.И. Курс физики, 1980 г., п.27,31.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.