Приборные погрешности обусловлены ограниченной точностью измерительных приборов.
Любым измерительным прибором нельзя измерить величину точнее, чем цена деления прибора. Приборная погрешность – объективная погрешность, от неё нельзя избавиться, её можно лишь уменьшить, выбирая более точный прибор.
Например: миллиметровой линейкой можно измерить размеры с точностью до 1 мм; штангенциркулем с точностью до 0,05 мм; микрометром с точностью до 0,01 мм и т. д.
Случайные погрешности обусловлены небольшими случайными изменениями измеренных значений физических величин.
Чем больше разброс измеренных значений физических величин при многократных измерениях, тем больше случайная погрешность и наоборот. К разбросу результатов измерений приводит влияние на саму величину и процесс измерения множество несущественных трудно учитываемых факторов.
Например: На измерение значения периода колебаний математического маятника (совокупность значений периода в зависимости от числа измерений изображена на рис 1) влияют колебания воздуха, не синхронность включение секундомера, начальные значения угла отклонения или сообщаемой скорости и т. д.
Случайная погрешность – объективная погрешность и оценивается при многократных измерениях методами теории вероятности.
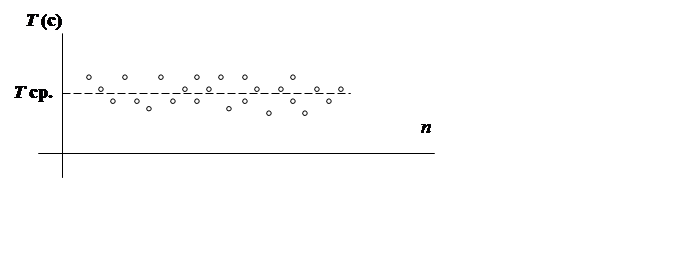
Рис 1. Зависимость измеренных значений периоде колебаний математического маятника от числа колебаний.
Систематические погрешности – погрешности связанные с несовершенством методов измерений (в частности, под этим имеются в виду ошибки, связанные с неотрегулированностью или неисправностью измерительных приборов, приближённостью законов используемых для расчёта измеряемых величин и т. д.) Систематические погрешности имеют объективный характер и, в отличие от случайных знакоопределены или меняются по определённому закону. Их можно уменьшить совершенствуя методы измерений, выбирая более точные законы для расчётов или учесть путём введения поправок к результату.
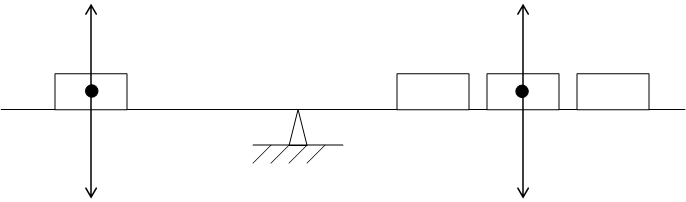
Например: а) при взвешивание в воздухе наличие выталкивающей силы Архимеда приводит к неточному определению массы. А именно (см. рис 2).
 |
|
|
|
|
Рис 2 Влияние выталкивающей силы на измерение массы тела.
Из рис. 2 следует, что не самом деле мы сравниваем не массу тела и разновесок, а равнодействующие сил тяжести и сил Архимеда т.е.
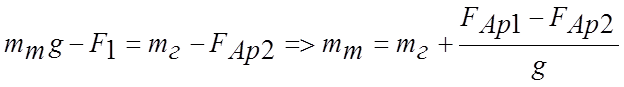 . (3)
. (3)
Величина ΔАFАр/g – есть та систематическая погрешность, которая вносится в результат измерения массы несовершенством данного метода;
б) при определении ускорения свободного падения по периоду колебаний математического маятника используется формула (3) не учитывающая затухание колебаний в следствии сопротивления среды, а измеряются затухающие колебания.
Грубые погрешности (промахи) – погрешности, вносимые в измерения человеком (человеческий фактор).
(Неправильно записали данные приборов, допустили ошибки в вычислениях и т. д.).
Как правило, эти ошибки велики и приводят к заметному искажению результатов. В этих случаях исключают ошибочные данные из последующего анализа или повторяют опыт.
Методы оценки погрешностей различных видов измерений составляют теорию погрешностей, основной задачей которой является оценка максимально допустимой ошибки в условиях данных измерений.
Далее мы ограничимся простейшим вариантом теории – линейной теорией погрешности.
Основными характеристиками погрешности (в рамках линейной теории) являются абсолютная и относительная погрешности.
Это размерная, положительная величина, характеризующая отклонение измеренного от истинного значений.
Относительная погрешность – это отношение абсолютной погрешности к истинному значению измеряемой величины.
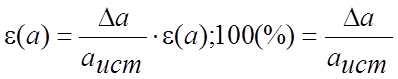 (5)
(5)
На практике вместо неизвестного истинного значения используют среднее значение измеряемой величины.
Формула (5) позволяет по известной одной из характеристик определить другую. Часто вначале удобнее найти относительную, а через неё абсолютную.
![]() .
.
Если измерение выполнено и погрешности определены, то окончательный результат записывается в виде
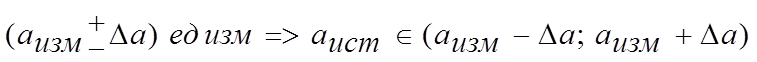 . (6)
. (6)
что эквивалентно заданию интервала, в котором лежит истинное значение искомой величины. И чем уже данный интервал, тем точнее измерения и наоборот.
4. Вычисление погрешностей.
За абсолютную погрешность однократно измеряемой величины применяют приборную погрешность.
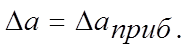
Для простых измерительных и цифровых приборов приборная погрешностьравная половине цены деления прибора.
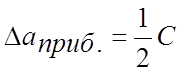 . (7)
. (7)
миллиметровой линейки (с=1 мм/дел) равна, Δапр = 0,5 мм.
штангенциркуля (с=0,05 мм/дел) – Δапр = 0,025 мм.
эл. секундомера (с=0,001 с/дел) – Δапр = 0,0005 с.
Для стрелочных электроизмерительных приборов приборная погрешность определятся через класс точности прибора (характеристика прибора указанная на его шкале).
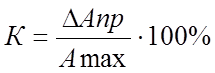 ,
(8)
,
(8)
представляющая собой отношение приборной погрешности к максимальному значению измеряемой прибором величины. Из (8) для приборной погрешности стрелочных электроизмерительных приборов получаем:
ΔАприб. = 0,01 · К · Аmax . (9)
Часто в расчетах приходится использовать физические и математические постоянные, которые как правило выражаются сложными десятичными дробями
(π= 3.141593… , е = 2.718282… , с = 2.99792… · 108 м/с
qe = 1,60219… · 10-19 Kл , mе = 1.67265… · 10-31к2 и т.д.).
При использовании постоянных мы вынуждены их округлять т.е. брать приближённые значения, это также даёт вклад в погрешность. К погрешностям табличных величин относятся так же как и к приборным.
За погрешность табличной величины принимают половину единицы последнего разряда табличной величины, выбранной с заданной точностью.
Например; при определении плотности тела цилиндрической формы необходимо использовать число π. Предварительно оговаривается точность расчётов (например вычисления проводят с точностью до
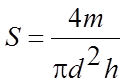
четырёх значащих цифр). Тогда используемое число π и погрешность Δπ соответственно будут равны:
π = 3.142, Δπ = 0.0005
и окончательная запись числа π с погрешностью имеет вид:
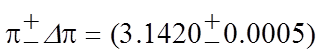
б) Погрешности многократно измеряемых величин.
Погрешности многократных измерений в рамках линейной теории оцениваются по следующей схеме
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.