Рівняння кола: План-конспект уроку математики

План-конспект уроку

Тема уроку: рівняння кола.

Тип уроку: засвоєння нового матеріалу.

Мета уроку:

*  навчальна: вивести рівняння кола, навчати учнів знаходити рівняння кола за його центром і радіусом, знаходити з рівняння кола його центр і радіус;

*  розвиваюча: розвиток абстрактно-логічного мислення, просторової уяви;

*  виховна: виховувати наполегливість, уважність при розв’язуванні математичних задач зокрема і при виконанні будь-якої роботи взагалі.

План проведення уроку

  I.  Організаційний момент (3 хв.);

  II.  Актуалізація опорних знань(10 хв.);

  III.  Засвоєння нового матеріалу (15 хв.);

  IV.  Розв’язування якісних задач і вправ (15 хв.);

  V.  Висновки, домашнє завдання (2 хв.).

Хід уроку                                      

І. Організаційний момент.

Вчитель заходить до класу, вітається з учнями, зосереджує їхню увагу, оголошує тему уроку.

ІІ. Актуалізація опорних знань.

1) Перевірка домашнього завдання. Вчитель викликає двох учнів, для того, щоб вони записали на дошці виконанні вправи з домашнього завдання    (№ 18, № 22).

2) Фронтальна робота з класом. Задача нашого уроку – вивести рівняння кола. Давайте спершу згадаємо, що таке коло. Коло – це фігура, що складається з усіх точок площини, рівновіддалених від даної (цю точку називають центром кола). Що ж таке радіус? Радіус – це відрізок, що сполучає будь-яку точку кола з його центром. Хорда кола – відрізок, що сполучає дві довільні точки кола. Діаметр – хорда, що проходить через центр кола. Кожний діаметр складається з двох радіусів, тому його довжина вдвічі більша від довжини радіуса.

ІІІ. Засвоєння нового матеріалу.

Отже, задача нашого уроку – вивести рівняння кола.

Насамперед з’ясуємо, що таке рівняння фігури взагалі. Рівнянням фігури на координатній площині називають рівняння з двома змінним, яке задовольняють координати будь-якої точки даної фігури і тільки вони. (Можливо учням треба пояснити зміст терміну „задовольняють”).

Давайте розглянемо випадки розміщення центра кола відносно початку координат і координатних осей (тут вчитель викликає до дошки двох учнів і прохає їх схематично зобразити декілька випадків розміщення кола):

§  центр співпадає з початком координат;

§  центр знаходиться на одній з осей координат;

§  центр не лежить на жодній з осей.  

Нехай на площині задано систему координат. Розглянемо випадок, коли центр кола радіуса R знаходиться в точці О (0; 0) – початку координат (рис.1). Нехай точка М (х; у) – довільна (біжуча) точка „нашого” кола. Знайдемо відстань між точками О і М. Скористаємось формулою відстані між точками:

                                           

або                                            . 

Але ж ОМ = R, тому

                                          .                                               (1)

Рівняння (1) є рівнянням кола радіуса R з центром в початку координат. 

Тепер, нехай маємо коло радіуса R  центром в точці А (а; b) і точку М (х; у) на колі (рис.2). Тоді, знову, за формулою відстані, маємо:

                                           

або                                            ,   

і оскільки AM = R, то              .                               (2)

Отже, рівняння (2) є рівнянням кола радіуса R з центром в точці А (а; b).

1^° Якщо відомі центр і радіус кола, то ми можемо написати його рівняння. Наприклад, рівнянням кола з центром в точці (3; 1) і радіусом 2 є рівняння

                                   .

2^° Якщо дано рівняння типу (2), то ми можемо вказати, якими є центр і радіус кола. Наприклад, якщо дано рівняння кола

                                   ,

то записавши його у вигляді (2), тобто

                                   ,

можна сказати, що центр кола – точка (-1; 2), а радіус – 3.                                                                       

ІV. Розв’язування якісних задач і вправ.

Отже, ми вивели рівняння кола і можемо з цього рівняння знайти центр і радіус кола. І навпаки – якщо дано центр і радіус кола, то ми можемо записати рівняння цього кола.

       Зараз ми і розв’яжемо кілька задач такого типу.

1. Запищіть рівняння кола з центром в початку координат радіуса: а) 3, ;    б) 4, .

Вчитель викликає до дошки двох учнів. У разі виникнення труднощів вчитель допомагає учням: оскільки центром кола є початок координат, то потрібно використати рівняння (1).      

2. Коло задано рівнянням . Які з точок А (0; -5), В (3; -4),            С (3; 2), D (; -) належать цьому колу? Побудуйте коло і точки на декартовій площині.

Тут потрібно скористатися означенням рівняння фігури: точки належать колу, якщо вони задовольняють його рівняння; підставляємо координати точок в рівняння і перевіряємо чи справджується рівність; для побудови кола на координатній площині проаналізуємо його рівняння – коло радіуса 5 з центром в початку координат.  

3. (№25) Дано точки А (2; 0) і В (-2; 6). Складіть рівняння кола, діаметром якого є відрізок AB.

На цей приклад бажано викликати до дошки більш сильнішого учня класу. Вчитель пояснює: для того, щоб знайти рівняння кола, потрібно знайти його центр і радіус; як відомо, радіус є половиною діаметра, який ми можемо знайти як відстань між точками A і B:

                                        ,

тоді                                         ,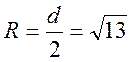

а центр кола можна знайти як середину відрізка AB, нехай С(с₁; с₂) – центр кола, тод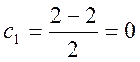і

                                                  і ,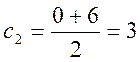

отже точка С має координати (0; 3); центр і радіус кола відомі, запишемо його рівняння:

                                                 ,

тобто                                       .

V. Висновки; домашнє завдання.

Отже, ми вивели рівняння кола і можемо записати його, якщо відомо центр і радіус цього кола; і можемо знайти центр і радіус кола, якщо відомо його рівняння.

§ 8, п. 74.

№ 26: Дано точки А (-1; -1) і С (-4; 3). Складіть рівняння кола з центром в точці С, що проходить через точку А.

№ 24: Знайдіть на колі, рівняння якого , точки: 1) з абсцисою 5; 2) з ординатою -12.    

Задача.  Визначте радіус кожного з кіл: а) ; б) ; в) .