Розробка відкритого уроку математики „Середня лінія трикутника”

середня школа №27

відкритий урок

„Середня лінія трикутника”

проведений у 8-А класі

вчителем математики

Гусєвою Л.С.

листопад, 2003р.

Тема: Середня лінія трикутника.

Розв’язування вправ.

Мета: продовжувати закріплювати поняття середньої лінії та її властивостей при розв’язуванні вправ, продовжувати вчити дітей знаходити середню лінію трикутника, розвивати логічне мислення, виховувати кмітливість, допитливість.

Тип уроку: урок розв’язування вправ.

Хід уроку.

І. Актуалізація опорних знань та умінь учнів.

Вчитель: Діти, сьогодні на уроці ми продовжуємо вчити середню лінію трикутника, її властивість, а також застосовувати їх при розв’язуванні вправ. Давайте повторимо ще раз, що ж таке середня лінія трикутника? Чому дорівнює середня лінія трикутника? Хотілося б почути доведення теореми (викликаю учня до дошки готувати доведення теореми). А ми, діти, в цей час перевіримо усно домашнє завдання по „збірника задач і контрольних робіт для 8 класу” А.Г. Мерзляка.

№81.

Знайти сторони трикутника, якщо його середні лінії дорівнюють 6см, 7см, 9см.

Розв’язання.

Оскільки, середня лінія трикутника дор. половині третьої сторони, то сторони даного трикутника відповідно рівні 12см, 14см, 18см.

Відповідь: 12см, 14см, 18см.

№82.

Периметр трикутника 18см. Знайти периметр трикутника, вершини якого середини сторін даного трикутника.

Розв’язання.

Оскільки середня лінія трикутника дор. половині третьої сторони, то периметр трикутника, утвореного середніми лініями дорівнює половині периметра даного трикутника, отже 9см.

Відповідь: 9 см.

№83.

Сторони трикутника відносяться як 3: 5: 7, а його периметр 60 см. Знайти периметр і сторони трикутника, вершини якого – середини сторін даного трикутника.

Розв’язання.

Нехай сторони даного трикутника 3х см, 5х см, 7х см. Оскільки периметр його 60 см, то маємо рівняння

3х+5х+7х=60

х=4 (см),

отже сторони даного трикутника 12см, 20см, 28. Оскільки середня лінія трикутника дор. половині третьої сторони, то сторони трикутника, утвореного середніми лініями будуть 6см, 10см, 14см, а периметр 30см.

Відповідь: 6см, 10см, 14см; 30см.

Вчитель: А тепер, діти, давайте послухаємо доведення теореми, яке підготував для вас учень.

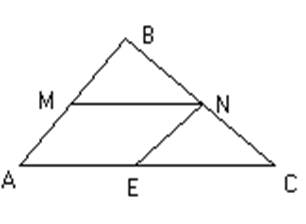Учень: Теорема. Середня лінія трикутника, яка сполучає середини двох бічних сторін трикутника, паралельна третій стороні і дорівнює її половині.

Дано:  – довільний трикутник

MN – середня лінія

Довести: MN || AC

MN=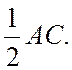

Доведення.

Нехай АВС – даний трикутник, N – середина сторони ВС. Через т.N проведемо пряму NM паралельну АС. За теоремою Фалеса т. М – середина сторони АВ, отже МN– середня лінія трикутника АВС і за побудовою вона паралельна АС.

Через т. N проведемо пряму NE || AB. За теоремою Фалеса т. Е – середина АС, отже АЕ=ЕС. Оскільки AMNE – паралелограм, то AE=EC=MN, тому MN=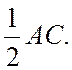

Вчитель. А тепер діти я пропоную розв’язати вам усні вправи.

Усні вправи.

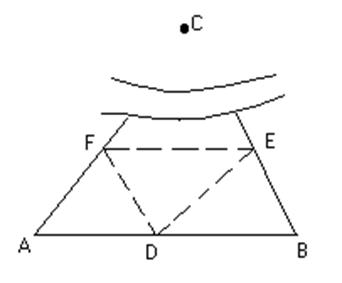
1.                                                Одна з вершин даної ділянки трикутної форми недоступна. Як вимірять периметр цього участка, використовуючи середню лінію трикутника.

Розв’язання.

Знайдемо точку D – середину сторони АВ і через точку D проведемо дві прямі, DE || AC і DF || BC, утворимо  Знайдемо периметр цього трикутника і збільшимо вдвічі.

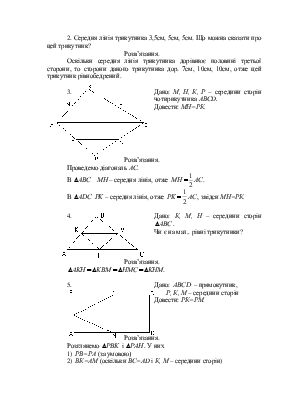
2. Середня лінія трикутника 3,5см, 5см, 5см. Що можна сказати про цей трикутник?

Розв’язання.

Оскільки середня лінія трикутника дорівнює половині третьої сторони, то сторони даного трикутника дор. 7см, 10см, 10см, отже цей трикутник рівнобедрений.

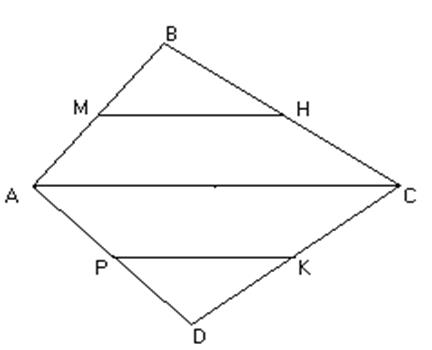
3.                                                  Дано: М, Н, К, Р – середини сторін чотирикутника АВСD.

Довести: МН=РК.

Розв’язання.

Проведемо діагональ АС.

В – середня лінія, отже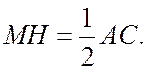

В – середня лінія, отже 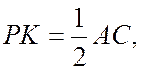 звідси МН=РК.

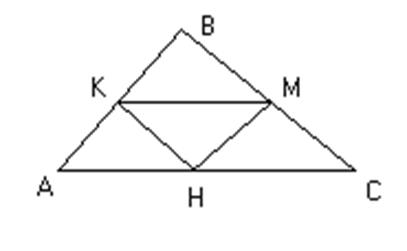
4.                                                  Дано: К, М, Н – середини сторін .

Чи є на мал.. рівні трикутники?

Розв’язання.

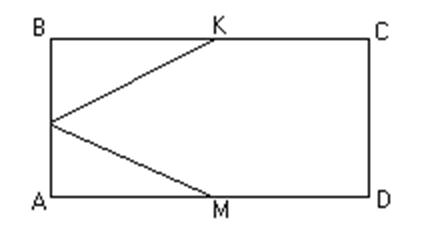5.                                                  Дано:  – прямокутник,              Р, К, М – середини сторін

Довести: РК=РМ.

Розв’язання.

Розглянемо  і  У них

1)  РВ=РА (за умовою)

2)  ВК=АМ (оскільки ВС=АD і К, М – середини сторін)

3) 

отже  (за І ознакою), тому РК=РМ.

ІІ. Самостійна робота.

Вчитель: А тепер, діти, що сидять на І варіанті виконують самостійну роботу №81, 82, 83 (ІІІ варіант), щоб переконатись, що ви дійсно зрозуміли домашнє завдання; а ті, діти, що сидять на ІІ варіанті слухають математичний диктант і на листочку виконують мал. до кожного твердження:

1)  протилежні кути паралелограма рівні;

2)  діагоналі паралелограма перетинаються і в точці перетину діляться пополам;

3)  бісектриса кута паралелограма відтинає від паралелограма рівнобедрений трикутник;

4)  бісектриси сусідніх кутів паралелограма перетинаються під прямим кутом;

5)  відрізки бісектрис протилежних кутів паралелограма паралельні;

6)  діагоналі ромба є бісектрисами його кутів;

7)  медіана, проведена з вершини прямого кута прямокутного трикутника, дорівнює половині гіпотенузи;

8)  якщо на одній стороні кута відкласти рівні відрізки і через їх кінці провести які завгодно прямі (непаралельні), то на другій стороні кута утворяться? Відрізки;

9)  середня лінія трикутника – це відрізок, що сполучає середини двох бічних сторін трикутника;

10)  можна побудувати відрізок, який не є середньою лінією трикутника, але він паралельний основі.

Вчитель. Закінчили, діти, роботу, а тепер я запрошую вас перевірити роботу своїх однокласників з малюнками, які знаходяться на зворотному боці дошки, а учні, які сидять на І варіанті, перевіряють свої відповіді із правильними відповідями, також записаними на зворотному боці дошки (при цьому учні міняються роботами, тобто проходить взаємоперевірка).

Після перевірки діти оголошують зароблені оцінки і здають роботи на повторну перевірку вчителеві.

ІІІ. Розв’язування вправ.

№87. Точки А і В лежать по різні сторони від прямої l на відстані 5см і 9см від неї відповідно. Знайти відстань від середини С відрізка АВ до прямої l.

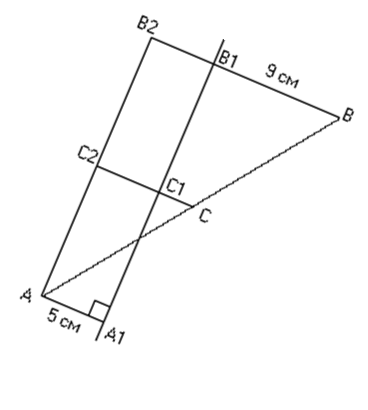Дано: пряму l,

см

см,

Знайти: –?

Розв’язання.

Продовжимо  Через т. А проведемо пряму || l, позначимо точки  тоді 5 см, звідси =9+5=14 см. Розглянемо  оскільки С – середина АВ, то за теоремою Фалеса – середина  отже –середня лінія  отже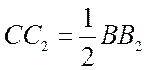

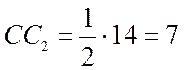(см).

(см).

Відповідь: 2 см.

IV. Вчитель: Ми закінчуємо урок, на якому ми продовжували вчити властивості середньої лінії трикутника, а також вчилися застосовувати ці властивості при розв’язуванні задач

Д/з №85, 86, 87 (ІІ в).