План – конспект уроку
Тема: розв’язування систем лінійних рівнянь способом підстановки.
Тип уроку: засвоєння нових знань.
Мета уроку:
· навчальна – навчити учнів використовувати спосіб підстановки при розв’язуванні систем лінійних рівнянь;
· розвиваюча – розвиток умінь пошуку ходу розв’язування будь-якої системи лінійних рівнянь з двома невідомими (за допомогою алгоритму);
· виховна – виховати в учнях акуратність, уважність, терплячість при виконанні будь-якої роботи.
План уроку:
1) Організаційний момент (2 хвилини);
2) Перевірка домашнього завдання (3 хвилин);
3) Актуалізація опорних знань (10 хвилин);
4) Засвоєння нового матеріалу (15 хвилин);
5) Розв’язування вправ (13 хвилин);
6) Домашнє завдання (2 хвилини).
Хід уроку
1) Організаційний момент.
Вчитель заходить до класу, вітається з учнями, перевіряє присутніх. Зосереджує увагу учнів.
2) Перевірка домашнього.
Вчитель з’ясовує з учнями які виникли труднощі при виконанні домашнього завдання. У разі їх виникнення вчитель із учнями (більш здібними) дає відповіді на питання; у разі виникнення нерозв’язаних прикладів, учні розв’язують їх біля дошки з повним поясненням (за допомогою вчителя).
3) Актуалізація опорних знань.
З метою повторення основних відомостей , які були засвоєні на попередніх уроках і які будуть необхідні при вивченні нового матеріалу, вчитель задає учням питання:
· Що таке система лінійних рівнянь ? (Рівняння утворюють систему, якщо потрібно знайти спільні розв’язки цих рівнянь);
· Що називається розв’язком системи рівнянь ? (Розв’язок системи рівнянь з двома невідомими – спільний розв’язок усіх її рівнянь (пара невідомих, при яких кожне рівняння системи перетворюється у правильну числову рівність));
· Що означає „розв’язати систему рівнянь” ? (Знайти всі її розв’язки або довести, що їх не існує);
· Які системи рівнянь називаються рівносильними ?
· У чому полягає графічний спосіб розв’язування систем лінійних рівнянь ?
Учні відповідають на питання; якщо при цьому у них виникають труднощі, то їм допомагають інші учні, а також вчитель.
4) Засвоєння нового матеріалу.
Вчитель зосереджує увагу учнів і акцентує її на новому матеріалі, який далі буде викладено вчителем.
Ми вже знаємо графічний спосіб розв’язування систем лінійних рівнянь. Але іноді цей спосіб використовувати не зручно і до того ж він дає наближені результати.
Тому при розв’язуванні систем лінійних рівнянь використовують і інші способи. Сьогодні ми розглянемо спосіб підстановки.
Розглянемо правильну рівність 7 + 2 = 9. Якщо у цій рівності число 2 замінити числовим виразом, значення якого дорівнює 2, то одержимо правильну рівність. Наприклад, значення виразу 3 – 1 дорівнює 2. Замінивши в рівності 7 + 2 = 9 число 2 цим виразом, одержимо правильну рівність 7 + (3 – 1) = 9. І навпаки, якщо у правильній рівності 7 + (3 – 1) = 9 вираз (3 – 1) замінити його значенням – 2, то одержимо правильну рівність 7 + 2 = 9.
На цих властивостях числових рівностей базується розв’язування систем лінійних рівнянь способом підстановки.
Розглянемо приклад. Розв’яжемо систему рівнянь
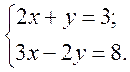 (1)
(1)
З першого рівняння системи виразимо y через x: y = 3 - 2x. Підставимо у друге рівняння системи замість y вираз 3 - 2x. Одержимо:
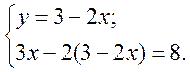 (2)
(2)
Дана і отримана система мають одні й ті ж розв’язки (є рівносильними). Друге рівняння системи (2) має лише одне невідоме x. Розв’яжемо його:
3x – 6 + 4x = 8;
7x = 14;
x =2.
У рівність y = 3 - 2x підставимо замість x число 2 і знайдемо відповідне значення y:
y = 3 – 2 · 2 = – 1.
Пара чисел (2 ; - 1) – розв’язок систем (1) і (2).
При розв’язуванні системи (1) ми замінили її системою (2). Ці системи називаються рівносильними (системи рівнянь, які мають одні й ті ж розв’язки, називаються рівносильними).
При розв’язуванні систем лінійних рівнянь способом підстановки потрібно:
· виразити з якого-небудь рівняння системи одне невідоме через інше;
· підставити в інше рівняння системи замість цього невідомого одержаний вираз;
· розв’язати одержане рівняння з одним невідомим;
· знайти відповідне значення іншого невідомого.
Зауваження: способом підстановки зручно користуватися тоді, коли коефіцієнт при якій-небудь змінній в рівнянні дорівнює 1.
5) Розв’язування вправ.
Вчитель викликає до дошки учнів і задає їм приклади. Учні, поки що з допомогою вчителя, розв’язують приклади, користуючись алгоритмом.
Приклади:
№ 822.
а)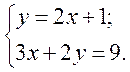
Підставимо у друге рівняння системи замість y вираз 2x + 1 і розв’яжемо одержане рівняння:
3x + 2(2x + 1) = 9;
3x + 4x + 2 = 9;
7x = 7;
x = 1.
Знаходимо відповідне значення невідомого у:
у = 2·1 + 1 = 3.
Відповідь: (1;3).
№ 823.
б)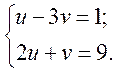
Виразимо з першого рівняння системи невідоме u через невідоме v:
u = 1 + 3v.
Підставимо у друге рівняння замість u вираз 1 + 3v і розв’яжемо одержане рівняння:
2(1 + 3v) + v = 9;
2 + 6v + v = 9;
7v = 7;
v = 1.
Знаходимо відповідне значення невідомого u:
u = 1 + 3·1 = 4.
Відповідь: (4;1).
Вчитель з учнями знову повторюють алгоритм.
6) Домашнє завдання.
№ 824: а) – в).
§ 6, п. 4.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.