Керування запасами. Проблеми керування запасами. Детерміновані моделі розміру партії, страница 3

Вираз (1.22) дозволяє безпосередньо визначити оптимальне значення множників Лагранжа. Це значення можна розглядати як призначені витрати, пов'язані з подачею заявок.

Випадок 3. Обмеження на капіталовкладення в керуванні запасами. Ця модель призначена для систем керування запасами, коли в кожний момент часу існує верхня межа Dкапіталовкладень у систему керування запасами. Обмеження в цьому   випадку має вид

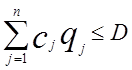
де  — вартість одиниці продукції j-го виду.

Потрібно мінімізувати вираження (1.14) при наявності обмеження (1.23). Обмеження (1.23) формально еквівалентно обмеженню на площу складу (1.16). Отже, можна записати

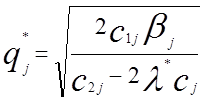
Імовірнісні  моделі при випадковому попиті

У попередньому розділі однією з визначальних умов при побудові моделей було допущення, що попит — заздалегідь відома визначена величина. Однак у багатьох реальних задачах попит є випадкова змінна, розподіл імовірності який будемо вважати відомим. У подібних ситуаціях здоровий глузд підказує, що для задоволення попиту, що перевищує очікувану потребу, необхідні додаткові запаси, що звичайно називають резервом.

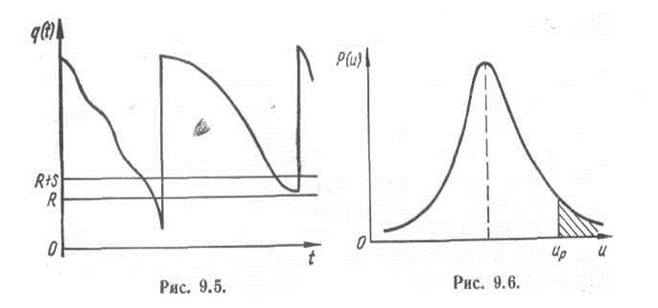
Стратегія керування запасами при імовірному  попиті може бути наступна. Створюється резерв Rв заздалегідь визначеному розмірі, а потім здійснюються чергові постачання запасів. Якщо в якийсь момент загальний запас знижується до розмірів резерву, негайно виробляється оформлення заявки на постачання нової партії. Якщо виконання запасу вимагає визначеного часу, то заявка на поповнення повинна бути оформлена, коли загальний запас знизиться до рівня R + s (мал. 1.5).

Таким чином, задача керування запасами в умовах невизначеності зводиться до визначення оптимального резерву R. Наявність великого резерву гарантує компенсацію будь-яких випадкових відхилень, що перевищують очікувану витрату, але спричиняє високі витрати збереження. Тому в основі розрахунку необхідного резерву лежить поняття так названого довірчого коефіцієнта, що представляє собою імовірність того, що потреба в запасах не перевищить наявного резерву. Значення довірчого коефіцієнта може бути рівним 95 % чи 99 %. Можна використовувати імовірність протилежної події — коефіцієнт ризику, рівний відповідно 5 % чи 1 %.

Коефіцієнт ризику виражає імовірність того, що потреби в запасах виявляться незадовільними через недостатній резерв.

Позначимо через Vпотреби в сировину між двома постачаннями і сформулюємо розглянуту задачу в такий спосіб.

Визначити таку величину резерву R щоб імовірність Р того, що резерв виявиться недостатнім, була рівна заданій величині р, тобто

P(V>q  + R) = p  або  P(V-q > R) = p      (1.24)

Для визначення величини R з (1.24) необхідно знати закон розподілу випадкової величини V.

Випадок 1. Потреба в запасах підпорядковується нормальному закону розподілу.

Припустимо, що випадкова величина Vрозподілена по нормальному законі з параметрами q і ².Позначивши

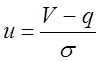
можна записати функцію щільності імовірностей

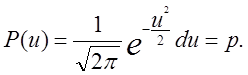
Задача полягає в перебуванні значення величини 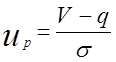, що залежить від імовірності р, для якого справедливa рівність

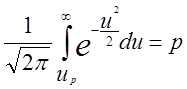    (1.25)

Якщо рівняння (1.25) представити графічно (мал. 1.6) то завдання полягає в знаходженні такого значення величини , щоб заштрихована ділянка під нормальною кривою в інтервалі (  ) був рівний  р.

За змістом прийнятих допущень резерв R повинний бути таким, щоб імовірність виникнення дефіциту дорівнювала p. Тоді з 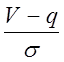> випливає, що резерв, який відповідає коефіцієнту ризику р, повинний дорівнювати щонайменше

R = V – q =

Тому

R =

Якщо, наприклад, р= 0,05, то  R= 1,64.

Викладене дозволяє зробити висновок, що розміри резерву R визначаються прийнятим коефіцієнтом ризику і коливаннями потреб у запасах, характерними середньоквадратичним відхиленням . Величину  можна оцінюючи визначити на основі статистичної обробки значень попиту в попередні періоди. Якщо позначити через  очікувану інтенсивність попиту, то загальні витрати на керування запасами складуть

.

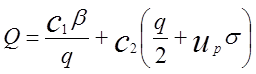Ці затрати мінімізуються, якщо

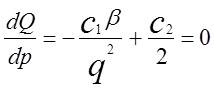
звідки отримамо значення оптимального розміру партії (так само, як і в п. 1.2), а саме

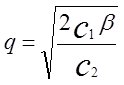
Звідси випливає, що на розмір партії величина резерву не робить впливу. Оптимальний запас разом з резервом дорівнює

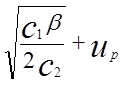
Випадок 2. Потреба в запасах підкоряється закону розподілу Пуассона. Якщо випадкова величина Vпідкоряється розподілу Пуассона, то відповідна імовірність виражається формулою

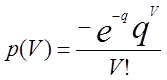
причому, як і в першому випадку, пропоноване значення випадкової величини дорівнює q.

Відомо, що якщо , то й розподіл Пуассона прагне до особливого роду нормального розподілу, очікування значення якого дорівнює q, a . Нескладні викладення   дозволяють одержати величину

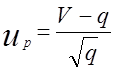
Отже, резерв R = . Сумарні  витрати на керування запасами складуть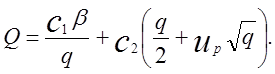 

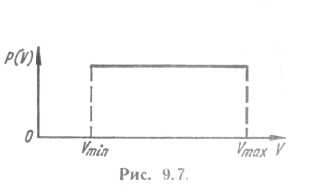Для   визначення   оптимального розміру   партії   знайдемо  і прирівняємо до нуля

Мал.1.7

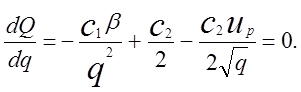
Вирішивши отримане рівняння четвертого степеня відносно q, визначимо оптимальний розмір партії.

У розглянутому випадку величина резерву залежить від оптимальних розмірів партії.

Випадок 3 Потреба в запасах підкоряється рівномірному  закону розподілу. Рівномірний розподіл випадкової величини V характеризується мінімальні  і максимальним значенням змінної V. У даних межах, за які змінна не виходить, щільність імовірності Р (V) постійна і її легко визначити

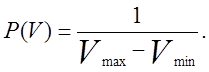
Визначимо тепер розміри резерву R, величина якого визначиться умовою

P( V – q > R) = p

У загальному випадку розміри резерву визначаються наступним  образом.  Позначимо  через таку крапку, що лежить на осі абсцис,  щоб   площа заштрихованого прямокутника праворуч від цієї абсциси  дорівнювала р. Тоді в відповідності з мал.1.7 маємо

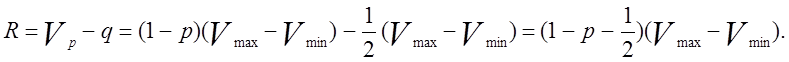
У підсумку

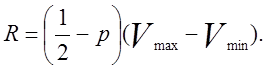       (1.26)

З формули (1.26) випливає, що при рівномірному розподілі імовірності розміри резерву прямо пропорційні різниці між  і

При рівномірному розподілі сумарні витрати на керування запасами складуть

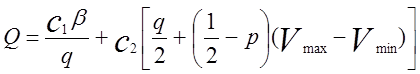
Ці витрати будуть мінімальні, якщо

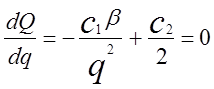
а це значить, що оптимальний розмір партії, як і у випадку нормального розподілу,  дорівнює

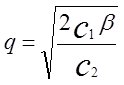
Якщо існує можливість визначити розміри втрат, зв'язаних з недостатністю резервів, то створюється основа для економічного аналізу і для[ 'визначення оптимального значення коефіцієнта  ризику.