Оптимальне значення qзнайдемо, узявши похідну від вираження (1.1) і прирівнявши її до нуля:
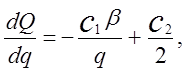
звідки оптимальний розмір постачання
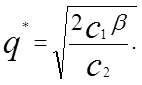 (1.2)
(1.2)
|
Використовувавши вираження (1.2), одержимо значення оптимального періоду між двома постачаннями
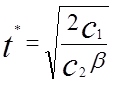 (1.3)
(1.3)
й оптимальними витратами
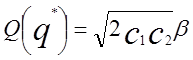 (1.4)
(1.4)
Однопродуктова статична модель з рівномірним поповненням запасу. У попередній моделі
передбачалося, що запас поповнюється миттєво, тобто всі qодиниць постачання надходять
одночасно. Тепер розглянемо складську систему типу
заводського складу. Зробимо припущення, що запас поповнюється рівномірно з інтенсивністю ![]() , для якої справедливa нерівність
, для якої справедливa нерівність ![]() .
.
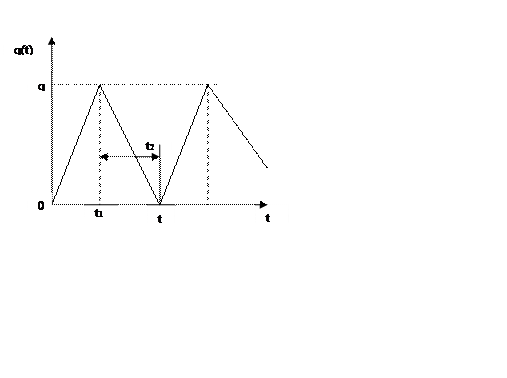
Для розглянутої моделі
протягом періодів виробництва чиста інтенсивність
поповнення запасів складає ![]() одиниць. Протягом
періодів простою інтенсивність споживання запасів
одиниць. Протягом
періодів простою інтенсивність споживання запасів ![]() одиниць. Графічно описувана модель
представлена на мал. 1.2. Тривалість виробництва
постачання
одиниць. Графічно описувана модель
представлена на мал. 1.2. Тривалість виробництва
постачання 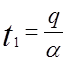 Наявний запас досягає
максимуму в момент закінчення виробництва
партії. Максимальний наявний запас
Наявний запас досягає
максимуму в момент закінчення виробництва
партії. Максимальний наявний запас
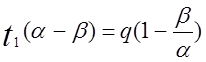 .
.
Час, необхідний для повної витрати наявного запасу,
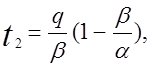
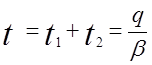 .
.
Загальнівитрати за одиницю часу при заданому значенні q складають
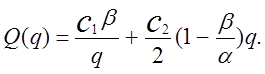 (1.5)
(1.5)
Знайдемо похідну від виразу (1.5) і прирвняємо її до нуля:
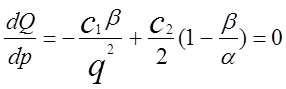 .
.
Звідси
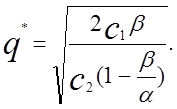 (1.6)
(1.6)
Однопродуктова статична
модель, що допускає дефіцит. Припустимо, що в моделі, розглянутої на с.3,
допускається дефіцит і питомі витрати
від дефіциту складають ![]() .
У цій моделі вимоги, що надходять при
дефіциті запасу, враховуються до моменту надходження постачання.
Передбачається, що при постачанні чергової партії запасів у першу
чергу задовольняються усі враховані вимоги, а потім решта.
.
У цій моделі вимоги, що надходять при
дефіциті запасу, враховуються до моменту надходження постачання.
Передбачається, що при постачанні чергової партії запасів у першу
чергу задовольняються усі враховані вимоги, а потім решта.
Нехай s — величина
дефіциту. Тоді після задоволення усіх врахованих
вимог наявний запас складе q - s. Це кількість запасу буде витрачено за час ![]() . Тривалість часу протягом
одного циклу, коли існує дефіцит, складе
. Тривалість часу протягом
одного циклу, коли існує дефіцит, складе ![]() .На мал.
1.3 показане поводження такої системи. Сумарні
витрати за одиницю часу визначаються виразом
.На мал.
1.3 показане поводження такої системи. Сумарні
витрати за одиницю часу визначаються виразом
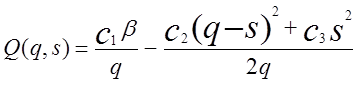 (1.7)
(1.7)
Прирівнюючи до нуля
похідні ![]() і
і ![]() ,
можна з рівняння (1.7) одержати
,
можна з рівняння (1.7) одержати
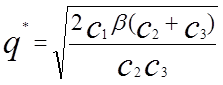 .
(1.8)
.
(1.8)
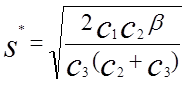 . (1.9)
. (1.9)
Загальна
однопродуктова статична модель. При побудові загальної детермінованої
моделі з усіх уведених раніше обмежень будемо враховувати тільки
одне — постійний за часом попит, вважаючи,
що час поповнення![]()
![]() запасів звичайно і
допускається дефіцит. З огляду на досить докладні викладення, виконані
при побудові попередніх моделей, у цьому розділі велика частина подібних перетворень
опускається. Відзначимо тільки, що побудова
моделі, як і раніше, виконується в три
етапи.
запасів звичайно і
допускається дефіцит. З огляду на досить докладні викладення, виконані
при побудові попередніх моделей, у цьому розділі велика частина подібних перетворень
опускається. Відзначимо тільки, що побудова
моделі, як і раніше, виконується в три
етапи.
1. Знаходиться вираження загальних витрат, віднесених до одиниці часу.
2. Це вираження спрощується за рахунок використання співвідношень між деякими перемінними з метою скорочення числа змінних у моделі.
3. Знаходяться значення інших змінних, мінімізуючі загальні витрати.
|
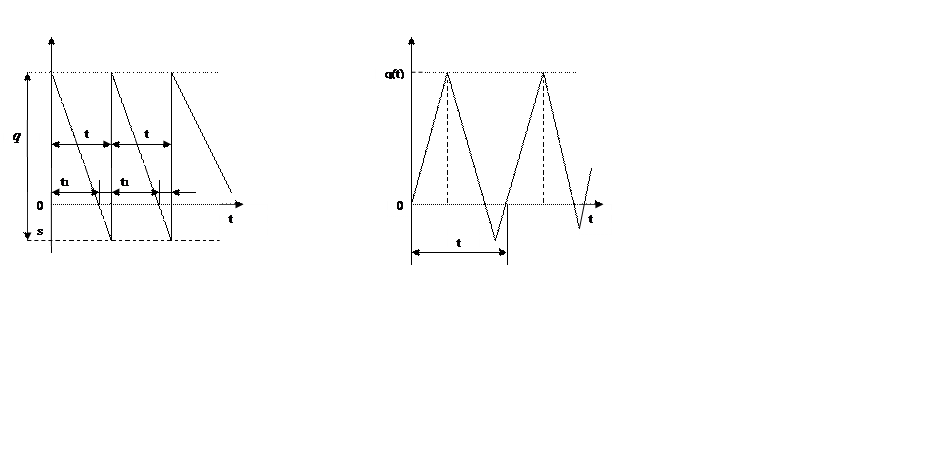
Розглянута модель наведена на мал. 1.4. Позначення ті ж, що й у попередніх моделях. Поєднуючи дві попередні моделі, неважко показати, що загальні витрати а одиницю часу складуть
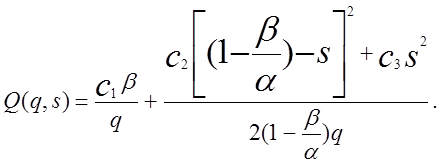 (1.10)
(1.10)
Прирівнюючи до нуля похідні ![]() і
і ![]() ,
можна зрівняння (1.10) знайти оптимальні значення для qі s. Не роблячи цих висновків, запишемо результати
,
можна зрівняння (1.10) знайти оптимальні значення для qі s. Не роблячи цих висновків, запишемо результати
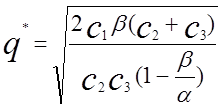 (1.11)
(1.11)
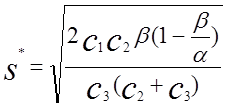 . (1.12)
. (1.12)
Багатопродуктова статична модель з обмеженнями. Практично на будь-якому складі зберігається велике число різних виробів і в рідшому випадку між ними відсутня взаємодія. Ця взаємодія може носити різний характер. Для промислових підприємств, наприклад, характерна ситуація, коли виробу можуть часково замінити один одного, можуть конкурувати при обмеженні на ємність складу. Може існувати верхня межа загального числа чи постачань максимальних капіталовкладень у запаси. У цьому розділі будуть розглянуті випадки, коли обмеження накладаються на ємність складу, число замовлень, на поповнення і максимальні вкладення в запаси.
Випадок 1. Обмеження на ємність складу. У даному випадку розглядається модель системи керування запасами, що включає n> 1 видів виробів, що зберігаються на одному складі з обмеженою ємністю.
Нехай А — максимально
припустима площа складського приміщення для пвидів. виробів
і що для j-го виробу
потрібнa площа, рівна ![]() . Якщо
. Якщо ![]() —
розмір постачання виробів j-го виду, тo повиннa виконуватися нерівність
—
розмір постачання виробів j-го виду, тo повиннa виконуватися нерівність
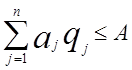 . (1.13)
. (1.13)
Припустимо далі, що запаси кожного виду
виробів поповнюються миттєво і дефіцит неприпустимий. Нехай ![]() ,
, ![]() і
і ![]() —
інтенсивність попиту, витрати на
оформлення постачання і витрати на збереження одного виробу за одиницю часу для j-го виду
виробів відповідно.
—
інтенсивність попиту, витрати на
оформлення постачання і витрати на збереження одного виробу за одиницю часу для j-го виду
виробів відповідно.
Сумарні витрати по всіх типах виробів складуть
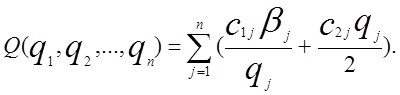 (1.14)
(1.14)
Необхідно знайти абсолютний мінімум Q по ![]() в інтервалі 0
<
в інтервалі 0
<![]() <
<![]() j=
j=![]() , урахуванням обмеження (1.13).
Спочатку вирішують задачу без обліку обмеження
(1.13), тобто визначають оптимальні розміри партій
для кожного типу виробів по формулі (1.2). Якщо обмеження (1.13) виконується, то воно є надлишковим і рішення задачі на цьому
закінчується. У противному випадку для визначення оптимальних
значень
, урахуванням обмеження (1.13).
Спочатку вирішують задачу без обліку обмеження
(1.13), тобто визначають оптимальні розміри партій
для кожного типу виробів по формулі (1.2). Якщо обмеження (1.13) виконується, то воно є надлишковим і рішення задачі на цьому
закінчується. У противному випадку для визначення оптимальних
значень ![]() може
бути використаний метод множників
Лагранжа, Складається функція Лагранжа
може
бути використаний метод множників
Лагранжа, Складається функція Лагранжа
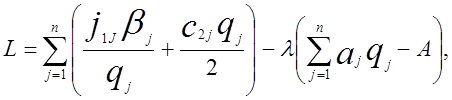
де ![]() — множник Лагранжа.
— множник Лагранжа.
Оптимальні значення q і ![]() можна знайти, прирівнявши
до нуля відповідні частки похідної, що дає
можна знайти, прирівнявши
до нуля відповідні частки похідної, що дає
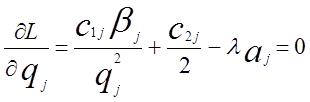
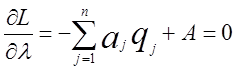 (1.15)
(1.15)
З першого рівняння випливає, що
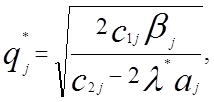 (1.16)
(1.16)
де ![]() — таке значення
— таке значення ![]() , при якому
, при якому ![]() , знайдене з виразу
(1.16), задовольняє (1.15).
, знайдене з виразу
(1.16), задовольняє (1.15).
Значення
![]() визначається
методом спроб і помилок.
визначається
методом спроб і помилок.
Випадок 2. Обмеження на загальне число замовлень. Зробимо допущення, що протягом планованого періоду може бути подано не більш до kзаявок на постачання запасів. Це означає, що
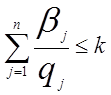 . (1.17)
. (1.17)
Якщо вважати, що фіксовані витрати, пов'язані з подачею заявок, дорівнють нулю, то сумарні витрати змісту
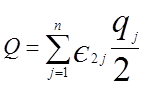 (1.18)
(1.18)
Потрібно знайти мінімум виразу (1.18) при обмеженні (1.17). Тому що в (1.18) враховуються тільки витрати на збереження, то обмеження (1.17) буде завжди істотним, тобто буде зроблене максимально можливе число замовлень, що дозволить скоротити витрати на збереження.
Для визначення оптимального
значення ![]() знову скористаємося методом множників Лагранжа,
для чого складемо функцію
знову скористаємося методом множників Лагранжа,
для чого складемо функцію
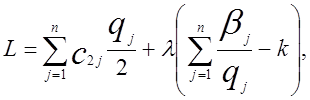
де ![]() —
множник Лагранжа. Тоді оптимальне значення повинне
задовольняти рівнянням
—
множник Лагранжа. Тоді оптимальне значення повинне
задовольняти рівнянням
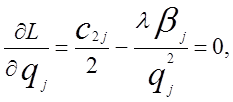 j=
j=![]() (1.19)
(1.19)
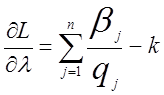 (1.20)
(1.20)
Оптимальним рішенням є
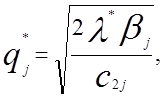
![]() (1.21)
(1.21)
звідки після підстановки (9.21) у (9.20) маєм
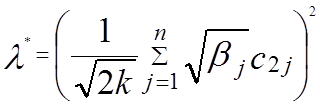 (1.22)
(1.22)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.