Керування запасами. Проблеми керування запасами. Детерміновані моделі розміру партії

КЕРУВАННЯ ЗАПАСАМИ

Керування запасами пов'язане з проблемою досягнення оптимальної рівноваги між двома конкуруючими факторами: мінімізацією капіталовкладень у запаси і максимізацією рівня обслуговування споживачів підприємства. Розмаїтість задач керування запасами призвело до створення великого числа математичних моделей, ефективне використання яких неможливо без застосування економіко-математичних методів і ЕОМ.

Моделі керування запасами розрізняються в залежності від характеру зміни вхідних у них величин. Якщо на процес керування запасами не впливають випадкові явища і його можна однозначно математично описати, то маємо детерміновану модель. У стохастичних моделях, навпаки, виявляються випадкові явища, що і є їхньою відміною ознакою. Самим істотним фактором, який необхідно враховувати при розробці моделей керування запасами, є час

Статичні моделі керування запасами, що істотно не залежать від часу, лише приблизно відповідають реальним умовам. Більш точне рішення може бути отримане за допомогою динамічної моделі, що враховує тимчасові зв'язки.

Проблеми керування запасами

Придатні до вживання, але не використовувані ресурси, у якості яких можуть виступати люди, матеріали, машини, гроші і т.д., називаються запасами.

Коли кількість ресурсів можна регулювати й існує хоча б одна стаття витрат, що убувають при збільшенні запасу, виникає задачакерування запасами, цільова функція якої зводиться до мінімізації загальних (фактичних чи очікуваних) витрат. Якщо ж запас впливає на попит, то цільова функція може виражатися в максимізації прибутку. Як у першому, так і в другому випадку для того, щоб одержати значення цільової функції, необхідно розглянути деякі вартісні показники. По-перше, існують витрати збереження запасів, що включають вартість капіталу, застарілого в запасах, витрати на зміст товару на складі й інші витрати, зв'язані з фізичною присутністю запасів. По-друге, існують витрати, зв'язані з роботою системи, куди входять витрати на подачу замовлень, витрати на ведення облікової документації, а також витрати на підготовчо-заключні операції, якщо розглядається випуск продукції партіями. Важливим показником також є витрати внаслідок чи дефіциту неможливості задовольнити попит.

До керованих змінних у задачах керувань запасами, які можна змінювати чи незалежно спільно, відносяться   такі.

1.   Обсяг ресурсів, що надходить, (у результаті закупівлі, чи виробництва за допомогою яких-небудь інших засобів). Цей показник може визначатися для ресурсу  кожного виду по чи окремості ж для цільового набору ресурсів. Так, наприклад, мова може йти про обсяги закупівель і виробництва незалежно один від  одного при деякому  спільному для них показнику.

2.   Чи частота терміни надходження ресурсів, тобто періодичність і моменти часу, є керованими змінними.

Наявність керованих змінних, що дають можливість використовувати альтернативні стратегії поводження, дозволяє розглядати задачі керування запасами, як задачі прийняття рішень, що дозволяють відповісти на два питання:

1)  скільки закуповувати (робити)?

2)  коли закуповувати (робити)?

Відповідь на перше питання визначає розмір запасу, на другий — крапку замовлення.

Для визначення розміру і крапки замовлення необхідно мінімізувати сумарні витрати системи керування запасами, що виражаються у виді функції, значення якої визначається наступними компонентами.

1.     Витрати на зміст запасу. Це витрати, що зростають   прямо   пропорційно збільшенню обсягу запасу і часу збереження.   Найбільш очевидною  складовою цих витрат, строго пропорційної рівню запасу і часу, є вартість капіталовкладень у запаси. Ця вартість визначається відсотком на вкладений капітал і для її обчислення часто потрібно проведення ретельних  досліджень.

Крім вартості капіталу необхідно приймати до уваги витрати на облік і адміністративні витрати. Запаси практично марні, якщо не відомо,  зберігається чи ні необхідний  виріб чи матеріал.

2.  Витрати на виконання замовлення. Цей вид витрат включає витрати, пов'язані з подачею замовлення постачальнику, чи витрати на виробничі потужності. У промисловості  ці   витрати   називаються   витратами   на   підготовчо-заключні операції і включають витрати праці й інші витрати,  пов'язані з поновленням виробничого періоду. Як правило, величина витрат по цій статті не залежить від розміру замовлення.

3.  Втрати від дефіциту. Витрати цього виду являють собою штраф, що включається підприємством у тому випадку, коли попит перевищує пропозицію. Дефіцит можна компенсувати екстреною доставкою, у цьому випадку розмір штрафу визначиться різницею між вартістю екстреної і вартістю звичайної доставки запасів. Можуть також мати місце і витрати, пов'язані зі змістом резервних виробничих потужностей, що використовуються тільки в  екстрених  випадках  для  ліквідації дефіциту.   Таке резервне устаткування може виявитися застарілим чи зношеним, у зв'язку з чим витрати його експлуатації можуть бути вищі, ніж для устаткування, використовуваного в звичайному режимі виробництва.

Прямі показники витрат унаслідок дефіциту можуть бути отримані тільки в деяких випадках і лише з обмеженою точністю.

Детерміновані моделі розміру партії

Побудова узагальненої моделі керування запасами, що враховує всі різновиди умов, що існують у реальності, пов'язано зі значними труднощями й у багатьох випадках задача виявляється аналітично нерозв'язною. У цьому розділі розглядаються моделі, що ілюструють різні підходи до рішення конкретних задач керування запасами.

Однопродуктова статична модель. Найпростіша модель керування запасами характеризується постійним за часом попитом, миттєвим поповненням запасу і відсутністю дефіциту. Процес зміни рівня запасів у часі при зроблених допущеннях показаний на малюнку 1.1

Мал.1.1

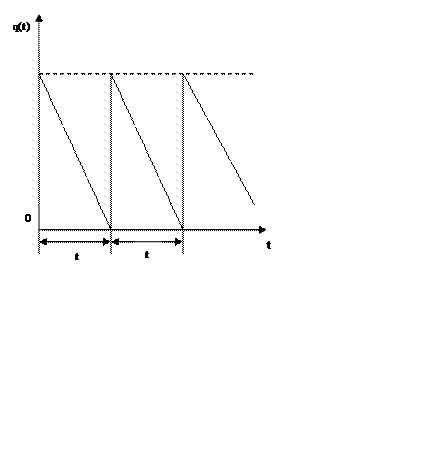
Для побудови математичної моделі введемо наступні позначення:  — інтенсивність попиту за одиницю часу;— витрати на оформлення замовлення, що не залежать від розміру замовлення і виникаючі всякий раз при його розміщенні;— витрати на збереження одиниці запасу в одиницю часу; — розмір постачання замовлення (розмір партії), Q(q) — сумарні витрати в одиницю часу, як функція q

З мал. 1.1 випливає, що середній рівень запасів між двома поставками дорвнює  а період часу 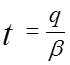. Звідси сумарні вирати на одницю часу

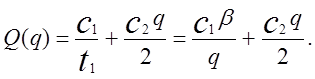    (1.1)