Застосування законів динаміки: Плани-конспекти урокiв з фізики, страница 5

Оскільки прискорення тіла за умовою дорівнює нулю, рівняння дру­гого закону Ньютона , має вигляд  . Оскільки тіло ковзає, сила тертя є силою тертя ковзання, і тому її модуль задо­вольняє рівність .

Запишемо рівняння другого закона Ньютона в проекціях на осі координат. У даному разі зручно напрямити вісь уздовж похилої площини вгору в напрямі сили , а вісь — перпендикулярно до по­хилої площини, як показано на кресленні.

У проекціях на осі координат дістанемо, с урахуванням співвідношен­ня , систему рівнянь:

    ,

    .

Розв'язуючи цю систему, дістанемо

2. Зісковзування тіла з похилої площини. Нехай тепер тіло зісковзує з похилої площини (рис. 2).

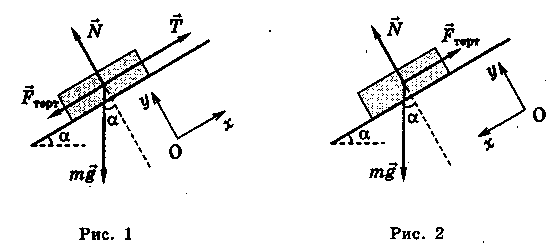
Будемо вважати, що нам відомі кут нахилу площини а і коефіцієнт тертя ц між тілом і площиною.

На тіло діють три сили: сила тяжіння , сила нормальної реакції і сила тертя ковзання , напрямлена вздовж похилої площини вгору.

Щоб знайти прискорення тіла, скористаємося другим законом Ньютона і виразом . У для сили тертя ковзання.

Записуючи другий закон Ньютона в проекціях на осі координат, дістанемо, з урахуванням співвідношення , систему рівнянь

   

   

З другого рівняння випливає, що . Звертаємо увагу: для тіла, розташованого на похилій площині, сила нормальної реакції є меншою, ніж сила тяжіння.

Підставляючи вираз для  у перше рівняння системи, знайдемо про­екцію прискорення .

Проаналізуємо одержану відповідь.

1. Швидкість бруска під час зісковзування буде збільшуватися, якщо  (у цьому випадку проекція прискорення має той самий знак, що й проекція початкової швидкості). З формули випливає, що для цього має виконуватися умова , тобто .

2. Швидкість бруска під час зісковзування буде зменшуватися, якщо  (у цьому випадку проекція прискорення має знак, протилежний знаку проекції початкової швидкості). Для цього має виконуватися умова , тобто .

3. Швидкість бруска під час зісковзування буде сталою, якщо . Для цього має виконуватися умова , тобто .

3. Рівновага тіла на похилій площині. Далі слід розглянути випадок рівноваги тіла на похилій площині. Коли тіло зісковзує по похилій пло­щині, його швидкість зменшується при . Якщо в початковий момент тіло було нерухомим, то при  воно так і залишиться в спокої. Воно залишиться в спокої також при . Отже, тіло може перебу­вати в спокої на похилій площині, якщо .

На завершення уроку можна розглянути з учнями таке питання: чому утримувати тіло на похилій площині легше, ніж тягти його вгору?

Домашнє завдання

Основне:

1.  К: § 28 (с. 100—101).

2.  Г: § 14 (14.4).

3.  1) 3 яким прискоренням з'їжджає хлопчик по слизькому обмерзлому схилу, якщо довжина схилу 13 м, а його висота 5 м? (36: 17.2)

2) Хлопчик (див. попередню задачу) потрапляє на ділянку схилу, посипану піском. Яким є прискорення хлопчика на цій ділянці, якщо коефіцієнт тертя дорівнює 0,3? (36: № 17.3)

3) Якщо один край метрової лінійки, що лежить на столі, підняти на 25 см, дерев'яний брусок зісковзує по лінійці зі сталою швидкістю. З яким прискоренням буде рухатися брусок, якщо висоту верхнього краю лінійки збільшити: а) удвічі; б) утричі? (36: № 17.4)

Додаткове:

1. Ф-9: § 39, 40.

2. 36: № 17.15, 17.16.'

УРОК 6/44. РОЗВ'ЯЗУВАННЯЗАДАЧНАРУХТІЛ ПОПОХИЛІЙПЛОЩИНІ

Метауроку:  з'ясуватирівеньзасвоєнняучнямививченогоматеріалу; навчитиїхзастосовуватисвоїзнаннядлярозв'язування конкретнихзадач.

Типуроку:  урокзакріпленнязнань.

Задачі, розв'язувані на уроці

Засвоєнню теоретичного матеріалу про рух тіла по похилій площині сприяють правильно організовані заняття з розв'язування задач. 1.    З яким прискоренням візок з'їжджає по похилих рейках, якщо ухил дорівнює 0,12, а коефіцієнт опору рухові  = 0,04 ? (36: № 17.1)

Необхідно роз'яснити учням, що ухил дорівнює синусу кута а нахи­лу дороги до горизонту. Якщо ухил є малим, можна вважати  = 1 (наприклад, якщо ухил дорівнює   0,1, одержуємо  = 0,995 = 1).

Розв'язання. На рис. 1 показано сили, що діють на візок, та обра­ні осі координат (таке обрання системи координат є зручним, оскільки вектор прискорення і дві з трьох сил напрямлені паралельно обраним осям).

Відповідно до другого закону Ньютона . У проек­ціях на осі ,. Як додатковим рів­нянням слід скористатися формулою . 3 одержаної системи рівнянь знайдемо . Згідно з умовою = 0,12, ( = 0,993 = 1). Відповідь: 0,78 м/с².

2. Кут  нахилу площини поступово збільшують від 0 до 90°. На площині лежить брусок масою . Коефіцієнт тертя дорівнює . Побудуйте графік залежності сили тертя  від кута . Чому дорівнює максимальне значення сили тертя ?(36: № 17.7) Розв'язання. Якщо кут а є малим, брусок залишиться в спокої, а якщо великим — буде зісковзувати. У першому випадку діє сила тер­тя спокою, у другому — сила тертя ковзання. У першому випадку . Цей випадок реалізується, якщо  (зазначимо, що якщо , то можливий рух зі сталою швидкістю). Якщо , тіло зісковзує з прискоренням; сила тертя ковзання . Таким чином, , якщо  і  , якщо . Графік залежності показано на рис. 2. 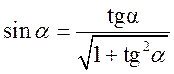З формули  випливає, що максимальне значення сили тертя . .

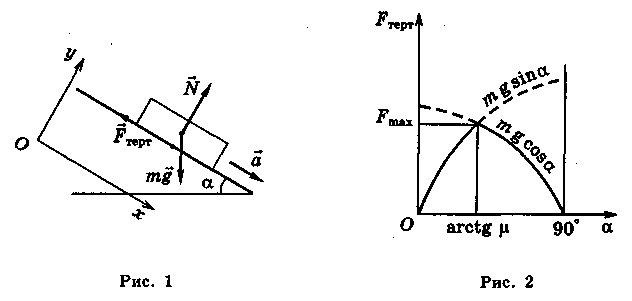
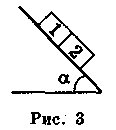
3.    Два бруски однакової маси, що дорівнює 0,2 кг, поставили на похилу площину з кутом нахилу 45° (рис. 3). Коефіцієнт тертя верхнього бруска об площину дорівнює 0,01, нижнього — 0,1. Визначте силу взаємодії брусків під час їх спільного зісковзування з похилої площини. {Відповідь: 0,63 Н.)

4.  Автомобіль масою 2 т підіймається по дорозі з ухилом 0,2. На ділянці шляху довжиною 32 м швидкість автомобіля зросла від 21,6 до 36 км/год. Вважаючи рух автомобіля рівноприскореним, визначте силу тяги двигуна. Коефіцієнт опору рухові 0,02. (Відповідь; 6,4 кН.)

5.  Санки штовхнули вгору по крижаній гірці, що утворює кут 30° із горизонтом. Санки заїхали на певну висоту і спустилися назад. Час спуску в 1,2 разу перевищує час підняття. Чому дорівнює коефіцієнт тертя? (Відповідь: 0,1.)