Застосування законів динаміки: Плани-конспекти урокiв з фізики, страница 3

б)     між переміщеннями, швидкостями та прискореннями тіл системи можуть існувати так звані кінематичні зв'язки. Наприклад, якщо тіла зв'язані натягнутою нерозтяжною ниткою, модулі переміщень цих тіл є однаковими.

2.     Приклади розв'язування задач. Два тягарі масами  і  з'єднані нерозтяжною ниткою, перекинутою через нерухомий блок. Якими є прискорення тягарів і сила натягу нитки, а також вага кожного з тягарів? Масами блока і нитки, а також тертям у блоці можна знехтувати.

Розв'язання. Почнемо з аналізу умови: зроблені в ній зауваження потребують деякого розшифрування.

Насамперед зазначимо, що, оскільки нитка є нерозтяжною, модулі переміщень тягарів за будь-який інтервал часу є однаковими: на скільки опустився один тягар, на стільки ж піднявся другий. Але якщо однакови­ми є модулі переміщень тягарів, то однакові й модулі їхніх швидкостей. А звідси випливає, що однакові й модулі прискорень тягарів. Оскільки тягарі рухаються в протилежних напрямах, швидкості тягарів  і  та прискорення і  задовольняють співвідношення  і . Це і є в даному разі врахування кінематичного зв'язку.

Зауваження «масами блока і нитки, а також тертям у блоці можна знехтувати» означає, що сила натягу нитки є однаковою в будь-якому її перерізі, тобто нитка діє на кожний із тягарів з однією і тією, ж (за мо­дулем) силою. У даному разі ці сили збігаються і за напрямом (обидві напрямлені вгору), тому позначимо їх однаково: .

Отже, на кожний із тягарів діють дві сили: сила тяжіння і сила реак­ції нитки .

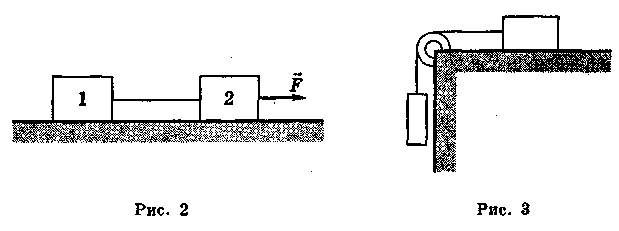
Зробимо креслення (рис. 1) і вкажемо на ньому всі ці сили, що діють на тягарі.

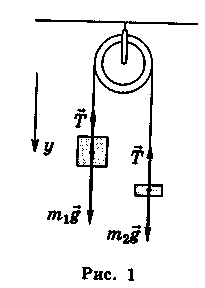
Рівняння другого закону Ньютона для тягарів мають вигляд:

, .

Оскільки всі сили та прискорення в даному разі напрямлені по вер­тикалі, можна розглядати проекції векторних величин Тільки на верти­кальну вісь. Напрямимо вісь у вертикально вниз і запишемо векторні рівняння, а також рівняння кінематичного зв'язку  у проекціях на цю вісь. Ми дістанемо систему трьох рівнянь:

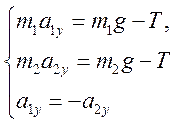
Підставимо у друге рівняння, а потім віднімемо почленно друге рівняння від першого.

У результаті дістанемо , звідки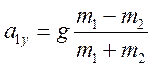

Оскільки , знаходимо .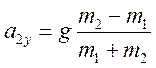

Якщо , то , . Таким чином, як і слід було очі­кувати, тягар із більшою масою рухається з прискоренням, напрямле­ним униз, а тягар із меншою масою — з прискоренням, напрямленим угору. Зазначимо, що про напрям швидкостей тягарів сказати нічого не можна, тому що початкові швидкості тягарів в умові не зазначено.

Скориставшись будь-яким із перших двох рівнянь системи, знаходимо силу натягу нитки: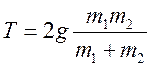

Щоб знайти вагу кожного з тягарів, ніяких нових обчислень робити не потрібно: достатньо пригадати, що вага -— це сила, з якою тягар роз­тягує підвіс. Отже, вага кожного з тягарів дорівнює за модулем силі

натягу нитки: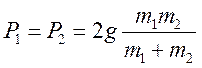

Необхідно привернути увагу учнів до того, що тягарі різної маси ма­ють однакову вагу. Це не повинне нас дивувати — адже обидва тягарі рухаються з прискоренням, причому прискорення тягарів напрямлені так, що вага більш масивного тягаря є меншою від сили тяжіння, а вага менш масивного — більшою.

Задачі, розв'язувані на уроці

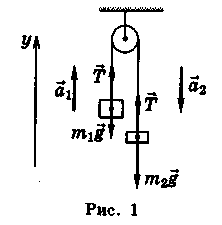
1.    По столу тягнуть сув'язь із двох тягарів, прикладаючи силу = 10 Н (рис. 2). Маси тягарів  = 800 г і  = 1,2 кг, коефіцієнти тертя об стіл відповідно  = 0,4 і = 0,2 . Знайдіть силу натягу нитки.

Розв'язання. Прикладена сила перевищує максимально можливу силу тертя спокою . Отже, бруски рухаються з прискоренням 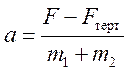. З формули  знаходимо, що 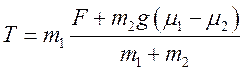. Відповідь: 5 Н.

2.     Якою є маса бруска, що лежить на столі (рис. 3), якщо підвішений тягар масою 100 г опускається з прискоренням 0,3 м/с²? Коефіцієнт тертя між бруском і столом дорівнює 0,3. (36: № 19.6)

Домашнє завдання

Основне:

1. К: § 28 (с. 102—103).

2. Г:§15(15.3).

3. 1) На нитці, перекинутій через блок, підвішено два тягарі масою 500 г кожний. Який додатковий тягар потрібно покласти на один із них, щоб система почала рухатися з прискоренням 50 см/с²? (36: № 19.2.)

2)   На нитці, перекинутій через невеликий блок, висять неру­хомо два однакові тягарі. На нижній тягар поклали важок масою 50 г. Якою є маса кожного з тягарів, якщо за 3 с відстань між ними збільшилася на 1,5 м? (36: № 19.3.) Додаткове:

1. Ф-9: § 39, 40.

2. 36: № 19.8, 19.10

УРОК 4/42. РОЗВ'ЯЗУВАННЯЗАДАЧНАРУХ СИСТЕМИЗВ'ЯЗАНИХТІЛ

Метауроку: з'ясуватирівеньзасвоєнняучнямививченогоматеріалу; навчитиїхзастосовуватисвоїзнаннявпроцесірозв'язу­ванняконкретнихзадач.

Типуроку:  урокзакріпленнязнань.

Задачі, розв'язувані на уроці

Теоретичний матеріал про рух системи зв'язаних тіл передбачає пра­вильно організовані заняття з розв'язування задач. У ході такого уроку особливо важливо звернути увагу на необхідність оптимізації співвідно­шення його дидактичних настанов зі змістовими особливостями розді­лу фізики, який вивчається.

1.  До нитки, перекинутої через нерухомий блок, підвішено тягарі ма­сами = 300 г і = 600 г. З якими прискореннями рухаються тягарі? Якою є сила натягу нитки? У скільки разів вага другого тя­гаря відрізняється від ваги першого? (36: № 19.1) Розв'язання. На рис. 1 покажемо всі сили, що діють на тягарі.

Запишемо рівняння другого закона Ньютона для кожного з тягарів у проекції на вісь у: ,  (у випадку невагомого шнура і невагомого блока без тертя, сила натягу шнура є скрізь однаковою). Скористаємося також кінематичним зв'язком: з нерозтяжності шнура випливає, що переміщення обох тягарів є однаковими за модулем; отже,

Звідси ,

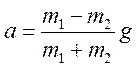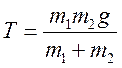
На прикладі цієї задачі слід показати учням два ефективні методи перевірки одержаного результату.

Перший з них — перевірка на симетрію. Очевидно, якщо поміняти тя­гарі місцями, натяг шнура і модуль прискорення тягарів мають не зміни­тися. Одержані для і вирази цій вимозі відповідають (якщо замінити ↔ значення не змінюється, а прискорення змінює тільки знак). Другий метод — перевірка на часткові та граничні випадки. Наприклад, якщо  прискорення має дорівнювати нулю, а . Якщо  має бути , (тягар 2 вільно падає і тому перебуває в стані невагомості). Одержані формули відповідають і цим вимогам. Вага обох тягарів є однаковою, хоч як значно відрізняються їхні маси: обидва тя­гарі діють на шнур з однаковими силами. Річ у тім, що вага меншого тягаря збільшується (прискорення цього тягаря напрямлене вгору), а вага більшого тягаря зменшується.