Педагогика \ Методика преподавания физики в средней школе

Вільне падіння. Рух тіла, кинутого під кутом до горизонту: Плани-конспекти урокiв з фізики, страница 4

1.  Із гвинтівки, встановленої горизонтально, роблять два постріли в мішень, установлену перпендикулярно до площини стрільби на відстані 100 м. Друга куля влучила на 1,7 см нижче від першої. Якою була швидкість другої кулі, якщо перша куля мала початкову швидкість 700 м/с? (Відповідь: 650 м/с.)

2.  Камінь кидають горизонтально з вершини гори, що має ухил . З якою швидкістю треба кинути камінь, щоб він упав на гору на відстані  від її вершини? (Відповідь: .)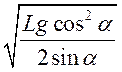

УРОК 20/20. РУХТІЛА, КИНУТОГОПІДКУТОМДОГОРИЗОНТУ

Метауроку: розвинутиуявленняучнівпрорухтілапопараболінапри­кладірухутіла, кинутогопідкутомдогоризонту.

Типуроку: комбінованийурок.

Демонстрації:   1. Рухтіла, кинутогопідкутомдогоризонту.

2. Дослідизіструменемводи, спрямованимпідкутомдогоризонту.

3. Залежністьдальностіпольотувідкутакидання.

Планвикладуновогоматеріалу:1. Траєкторіярухутіла, кинутогопідкутомдогоризонту.

2.  Час, висотаідальністьпольотутіла, кинутогопідкутом догоризонту.

3. Залежністьдальностіпольотувідкутакидання,

Перевірка знань

Самостійна робота № 11 «Рух тіла, кинутого горизонтально».

Виклад нового матеріалу

1.  Траєкторія руху тіла, кинутого тд кутом до горизонту. Для того щоб учні мали уявлення про траєкторію руху тіла; кинутого під кутом до горизонту, треба провести кілька дослідів зі струменем води, що витікає з наконечника гумової трубки, з'єднаної з водопровідним краном. Струмінь показує траєкторію руху частинок води, випущених із наконечника гумової трубки під кутом до горизонту. Форма струменя — парабола. Таким чином, траєкторією руху тіла й у цьому разі буде парабола. Однак тепер вершина параболи — точка, що відповідає підняттю тіла на максимальну висоту.

2.  Час, висота і дальність польоту тіла, кинутого під кутом до горизонту. Нехай тіло кинуто зі швидкістю і>0 під кутом а до горизонту. Сумістимо початок координат із початковим положенням тіла, напря­мимо вісь вертикально вгору, а вісь — горизонтально.

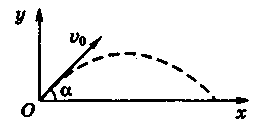
Оскільки й у цьому разі одержуємо:

, ;

,

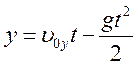
Тут , .

Коли тіло перебуває на максимальній висоті, його швидкість напрям­лена горизонтально, тобто проекція швидкості на вісь дорівнює нулю.

Оскільки , для часу підняття тіла на максимальну висоту одер­жуємо:

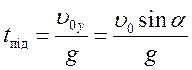
Знаючи час підняття тіла, нескладно знайти й висоту, на яку воно підійметься: для цього досить підставити в формулу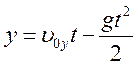 час  У результаті дістанемо:

.

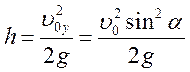Наприкінці руху тіло повернулося на початкову висоту, тобто .

Оскільки 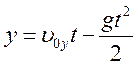, одержуємо 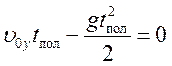. Оскільки , звідси випливає:

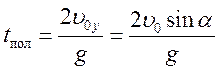
Очевидно, що час польоту є у два рази більшим від часу підняття, тобто час підняття дорівнює часу спуску. Знайдемо тепер дальність польоту.

Оскільки , одержуємо 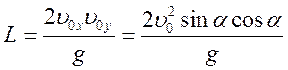. Скориставшись формулою , одержуємо:

.

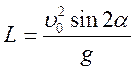3. Залежність дальності польоту від кута кидання. З'ясуємо, під яким кутом потрібно кинути тіло, щоб воно впало якнайдалі. З виразу для дальності польоту 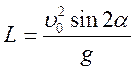 випливає, що для заданого значення максимальна дальність польоту досягається, якщо макси­мальним є значення . Найбільше значення синуса дорівнює 1(у кута 90°). Таким чином, , звідки . Отже, максимальна дальність польоту досягається якщо , і дорівнює:

.

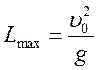Питання до учнів у ході викладу нового матеріалу

1.  Чи можна рух тіла, кинутого під кутом до горизонту, вважати рівноприскореним?

2.  Що спільного в русі тіл, кинутих вертикально вгору і під кутом до горизонту?

3.  У якій точці траєкторії тіло має найменшу швидкість?

4.  У якій точці траєкторії прискорення тіла напрямлене перпендикулярно до його швидкості?

Задачі, розв'язувані на уроці

1.  Тіло, кинуте під кутом 30° до горизонту, упало в певну точку на поверхні землі. Під яким іншим кутом потрібно кинути друге тіло з тією ж початковою швидкістю, щоб воно впало в ту саму точку, що й перше? (Відповідь: 60°.)

2.  Під яким кутом до горизонту кинуто тіло, якщо дальність польоту вдвічі перевищує максимальну висоту? (36: № 8.18. Відповідь: 63°.)

3.  Кинутий під кутом до горизонту м'яч сягнув висоти 20 м. Скільки часу він був у польоті? (36: № 8.20. Відповідь: 4 с.)

До конспекту учня

Висота підняття тіла, кинутого зі швидкістю v0 під кутом а до го­ризонту:

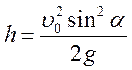
Дальність польоту тіла, кинутого зі швидкістю  під кутом  до горизонту:

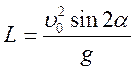
Максимальна дальність польоту 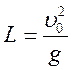 досягається, якщо .

Домашнє завдання

Основне:

1.  Г: § 7 (7.4).

2.  1)   Камінь кинуто зі швидкістю 30 м/с під кутом 60° до горизонту. Якими є швидкість і прискорення каменя у верхній точці траєкторії? (36: № 8.19)

2)  Снаряд випущено зі швидкістю 800 м/с під кутом 30° до горизонту. Якою є тривалість польоту снаряда? На яку висоту підіймається снаряд? На якій відстані від гармати він упаде на землю? (36: № 8.22)

3)  3 якою початковою швидкістю і під яким кутом до горизонту випущено снаряд, що був у повітрі 30 с і впав на відстані 6 км від гармати? (36: № 8.24)

3.           Д: підготуватися до самостійної роботи №12.

Додаткове:

1. Ф-9: § 35.

2. 36: № 8.34, 8.35.

Самостійна робота №12

«Рух тіла, кинутого під кутом до горизонту»

Початковий рівень

1.  Чи залежить дальність польоту тіла від напряму початкової швидкості?

2.  При якому куті кидання дальність польоту буде найбільшою?

Середній рівень

1.  М'яч було кинуто під кутом 30° до горизонту з початковою швидкістю 20 м/с. Якою була дальність польоту? (Відповідь: 35 м.)

2.  Снаряд, що вилетів із гармати під кутом до горизонту, був у польоті 12 с. Якої найбільшої висоти сягнув снаряд? {Відповідь: 180 м.)

Достатній рівень

1.  Камінь, кинутий під кутом 30° до горизонту, двічі був на одній висоті: через 3 с і через 5 с після початку руху. Визначте початкову швидкість і максимальну висоту. (Відповідь: 78,4 м/с; 73,5 м.)

2.  Камінь кинуто під кутом 30° до горизонту зі швидкістю 10 м/с. Через який час камінь буде на висоті 1 м? (Відповідь: 0,28 с; 0,74 с.)

Високий рівень

1.  Камінь, кинутий під кутом до горизонту, впав на землю через 4 с. Чому дорівнюють висота і дальність польоту каменя, якщо відомо, що під час руху його максимальна швидкість була вдвічі більшою від мінімальної? (Відповідь: 20 м; 45 м.)

Скачать файл