Полтавський державний педагогічний університет
ім. В.Г.Короленка
Фізико-математичний факультет
Кафедра математичного аналізу та інформатики
Властивості бета та гамма функцій Ейлера
Курсова робота студентки гр.М-41 денної форми навчання
Одай Людмили Олександрівни
Науковий керівник: кандидат фізико-математичних наук доц. Губачов Олександр Павлович
Полтава - 2004
Змiст
Вступ 3
§1 Бета функцiя. 4
§2 Властивостi Ейлерової функцiї бета. 5
§3 Гамма функцiя. 7
§4 Властивостi Ейлерової функцiї гамма. 9
§5 Звязок мiж бета i гамма функцiями. 11
§6 Приклади. 14
§7 Наближене обчислення Ейлерових функцiй на ЕОМ. 16.
Таблицi для наближених обчислень функцiї гамма. 18
Графiк функцiї гамма. 22
Висновки. 23
Список лiтератури. 24
У прикладній математиці існуєвелика кількість задач , які можна розв’язувати за допомогою спеціальних функцій , а наявність ЕОМ помітно полегшує роботу з останніми .
У даній курсовій роботі ми розглядаємо спеціальні Ейлерові функції бета та гамма. Для початку вводимо їх означення . Вивчаємо властивості цих функцій. Розглядаємо взаємодію між функціями бета та гамма, тобто вираження однієї функції через іншу. Наводимо деякі конкретні приклади використання вище вказаних функцій. Та розглядаємо їхні графіки.
А також , висвітлюємо проблему наближеного обчислення Ейлерових функцій бета та гамма на ЕОМ. Ця проблема на сьогодення є актуальною. Адже, все більше популярними стають методи роботи , при яких аналітичні операції виконуються на ЕОМ; природним є те, що при цьому роль спеціальних функцій дуже велика. Отже, на даний час математичне забезпечення будь-якої сучасної ЕОМ повинно включати велику кількість стандартних програм для роботи з багатьма класами спеціальних функцій.
§1 Бета функція Ейлера.
Інтеграл Ейлера першого роду. Так називається (за пропозицією Лежандра) інтеграл виду
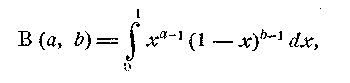 |
(1)
де а, b>0. Він представляє функцію,що залежить від двох змінних параметрів а і b, i називається бета функцiєю Ейлера.
Розглянутий інтеграл, як ми знаємо, для додатніх значень а і b (хоча б для тих , які менші одиниці) збігається і, отже, дійсно може бути покладений в основу визначення бета функції.
§ 2 Властивості Ейлерової функції бета.
1.В (а, b) = B(b, а),
Доведення:
насамперед, майже безпосередньо (підстановкою х=1 — t) одержуємо:
В (а, b) = B(b, а),
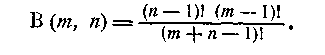 так що функція В є
симетричною відносно а і b.
так що функція В є
симетричною відносно а і b.
2°.
Доведення:
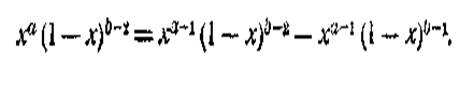 За допомогою інтегрування за частинами з формули (1),
при b>1, знаходимо: Ми
використовуємо при цьому тотожність
За допомогою інтегрування за частинами з формули (1),
при b>1, знаходимо: Ми
використовуємо при цьому тотожність
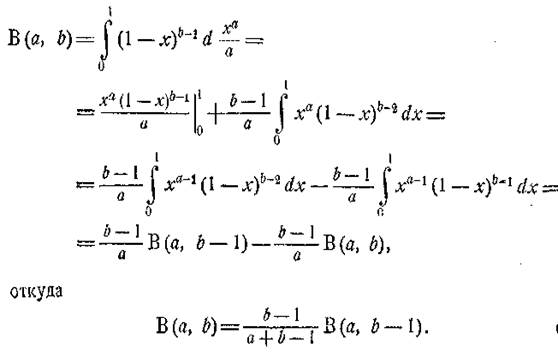
(2)
Цю формулу можна застосовувати з метою зменшення b, поки b залишається більше 1; у такий спосіб завжди можна досягти того, щоб другий аргумент став < або = 1.
Утім, того ж можна досягти й у відношенні першого аргументу, тому що через симетричність бета функцiї — має місце й інша формула:
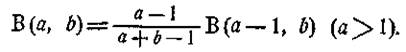 |
|
Якщо b дорівнює натуральному числу п, то, послідовно застосовуючи формулу (2), знайдемо:
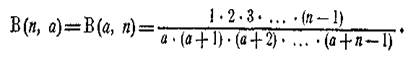 Тому
для бета функцiї (а, п)і — одночасно —
для бета функцiї (n, а) отримуємо остаточний вираз
Тому
для бета функцiї (а, п)і — одночасно —
для бета функцiї (n, а) отримуємо остаточний вираз
(3)
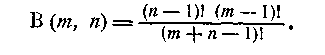 Якщо й а дорівнює натуральному числу т,
то
Якщо й а дорівнює натуральному числу т,
то
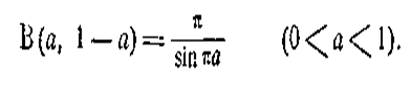 Цю
формулу можна застосовувати і при т=1 чи п=1, якщо під символом
0! розуміти 1.
Цю
формулу можна застосовувати і при т=1 чи п=1, якщо під символом
0! розуміти 1.
3.
Доведення:
дамо для функції бета інше аналітичне представлення, що часто буває корисно. Саме, якщо в інтегралі (1) зробити підстановку х= y/(1+y) , де у — нова змінна, що змінюється від 0 до нескінченності , то одержимо
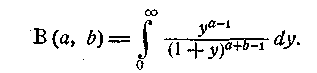 |
(4)
поклавши тут b=1-а (з припущенням, що 0<а<1), знайдемо
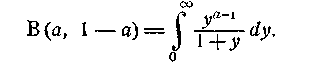 |
Ми впізнаємо вже обчислений інтеграл, який також пов’язаний з ім'ям Ейлера. Підставляючи його значення, приходимо до формули
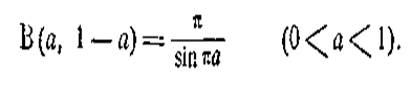 |
(5)
Якщо, зокрема, узяти
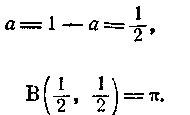 |
то отримаємо
Ми обмежимося цими властивостями функції бета тому, що — як побачимо нижче — вона дуже просто виражається через іншу функцію — гамма, на якій ми зупинимося докладніше.
§3 Гамма функція.
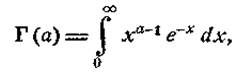 Інтеграл Ейлера другого роду. Ця назва була надана Лежандром чудовому
інтегралу:
Інтеграл Ейлера другого роду. Ця назва була надана Лежандром чудовому
інтегралу:
(6)
який збігається при будь-якому а > 0 (при а < або = 0 інтеграл розбіжний) і визначає функцію гамма Ейлера. Функція гамма, після елементарних, є однієї з найважливіших функцій для аналізу і його додатків. Вивчення властивостей функції гамма, виходячи з її інтегрального означення (6), послужить одночасно і прекрасним прикладом застосування викладеної теорії інтегралів, що залежать від параметра.
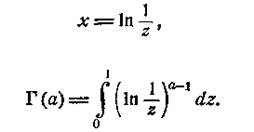 Якщо покласти в (6)
Якщо покласти в (6)
Як відомо ,
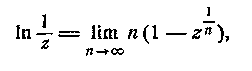
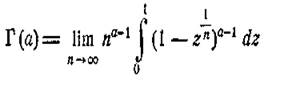 причому вираз n(1—z1/n) при
зростанні п прямує до своєї границі зростаючи *). У такому випадку,
причому вираз n(1—z1/n) при
зростанні п прямує до своєї границі зростаючи *). У такому випадку,
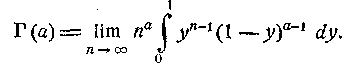 чи — якщо
застосувати підстановку z=y":
чи — якщо
застосувати підстановку z=y":
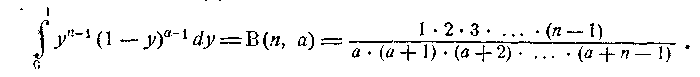 але згідно з (3)
але згідно з (3)
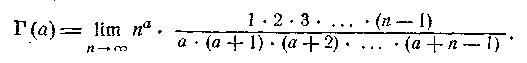 Таким чином,
остаточно, приходимо до знаменитої формули Ейлера — Гаусса:
Таким чином,
остаточно, приходимо до знаменитої формули Ейлера — Гаусса:
Цю формулу Ейлер ще в 1729 р. повідомив у листі до Гольдбаха, але вона була забута. Гаусс саме її поклав згодом в основу самого визначення функції
*) В цьому можна переконатися методами диференційного числення , розглядаючи вираз 1-zα/α як функцію від α .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.