Властивості бета та гамма функцій Ейлера, страница 2

П(а) = Г(а+1). Багато займалися функцією гамма Лежандр і Лобачевський, причому Лобачевський виходив зі своєрідного означення функції гамма, що використовує нескінченні ряди.

 § 4 Властивості Ейлерової гамма функції.

1.  Функція гамма, при •всіх значеннях а > 0, неперервна і має неперервні  похідні всіх порядків.

Доведення:

досить довести лише існування похідних. Диференціюючи інтеграл (6) під знаком інтеграла, одержимо

 

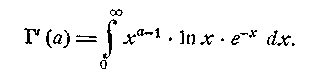(7)

Застосування   правила   Лейбніца   виправдане тим,   що   обидва інтеграли

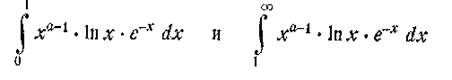збігаються рівномірно відносно а: перший при х = 0 для а>=а₀>0 (мажоранта x^ao~l|Inx|), а другий при х = ∞ для a<= А<∞ (мажоранта х^А е-^х(для х>0,очевидно, lnx<x)).

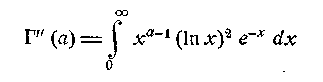Таким же   шляхом   можна переконатися   й   в   існуванні другої похідної

(7*)

і всіх подальших.

2. Функціягамма є природним поширенням на область будь-яких додатніх значень аргументу — функції п!, визначеної лише для натуральних значень п.

 

Доведення:

З (6), інтегруванням по частинах, одразу отримуємо:

 

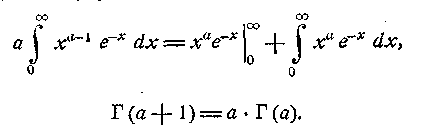(8)

Ця формула, при повторному застосовані, дає

Г(а + n) = (а+n - 1)-(a + n — 2)- ... . (a + 1) • а Г (а). (8*)

Таким шляхом обчислення гамма функцiї для довільного значення аргументу а може бути приведене до обчислення функцiї гамма для 0<a<=l (чи, якщо завгодно, для 1 < a <=2).

Якщо в (8*) взяти а = 1 і взяти до уваги, що

 

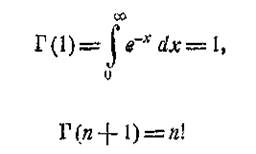(9)

то виявиться, що

(10)

3. Хід зміни функції гамма. Тепер ми можемо скласти собі загальне уявлення про поведінку функції гамма при зростанні а від 0 до ∞.

З (9) і (10) маємо: Г(1) -Г(2)= 1, так що, за теоремою Ролля, між 1 і 2 повинен лежати корінь a₀ похідної Г (а). Ця похідна постійно зростає, тому що друга похідна Г" (а), як видно з виразу (7*), завжди додатня. Отже, при 0<а<а похідна Г'(а)<0, і функція Г (а) спадає, а при а₀<а<∞ буде Г'(а)>0, так що Г (а) зростає; при а = а₀ у наявності мінімум. Обчислення, якого ми не проводимо, дає:

а₀ = 1,4616 ..., min Г (а) = Г (а₀) = 0,8856...

Цікаво установити ще границю для Г (а) при прямуванні а до 0 або до ∞. З (8) та з властивості 1 ясно, що

 

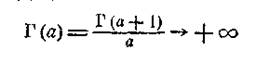при а→+0. З іншого боку, з формули (10),

Г(а)>n!, лише тільки а>n+1, тобто Г (а) →+ ∞ і при а →+ ∞.

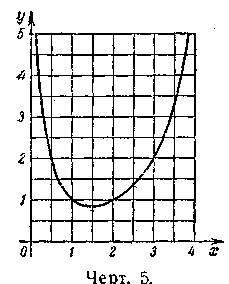Графік функції гамма (а) представлений на малюнку 5.

§ 5 Зв'язок між бета i гамма функціями.

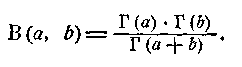1.

Доведення:

для того щоб з’ясуватити цей зв'язок, ми підстановкою x = ty(t>0) перетворимо (6) до виду:

 

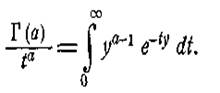(11)

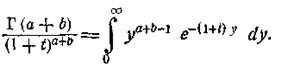
Заміняючи   тут а на а+b і одночасно t на 1+t, одержимо:

Помножимо тепер обидві частини цієї рівності на t^a-1   і  проінтегруємо по t від 0 до ∞:

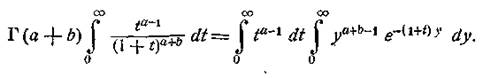В інтегралі ліворуч ми впізнаємо функцію В (а, b); праворуч же переставимо інтеграли. У результаті одержимо [з урахуванням (7) і (6)]:

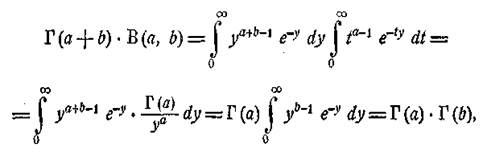
звідкіля, нарешті,

 

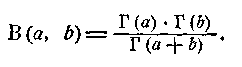(12)

Наведене витончене доведення цього співвідношення Ейлера належить Діріхле. Утім, для його обґрунтування слід ще виправдати перестановку інтегралів.

Ми зробимо це, обмежуючи спочатку припущенням що a>1, b>1. Тоді для функції

яка неперервна (і притому додатна) для y>=0 і t>=0, a інтеграли у свою чергу представляють собою неперервні функції: перший — від t для t>=0, другий — від у для у >=0. Посилання на теорему виправдують перестановку інтегралів, а з нею і формулу (12) — для випадку a>1, b>1.

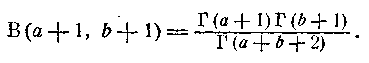Якщо ж   відомо лише,   що а>0  і  b>0,  то — по доведеному— маємо

А звідси, використовуючи формули приведення (2), (2^’) для функції В і (8) для функції гамма, легко знову одержати формулу (12), вже без непотрібних обмежень.

2. Формула доповнення.

Якщо у формулі (12) покласти b=1-а(вважаючи 0<а<1), то, враховуючи (5) і (9), одержимо співвідношення

 

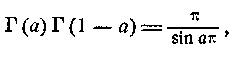(13)

яке і називається формулою доповнення.

При a =1/2 звідси знаходимо (так як Г(а)>0):

 

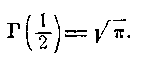(14)

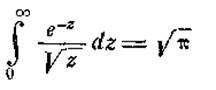
Виконавши в інтегралі

підстановку   z = х²,    ми   знову  одержимо  уже   відомий  нам   інтеграл

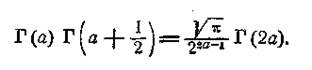
3. Формула Лежандра.

Доведення:

Якщо в інтегралі зробити підстановку

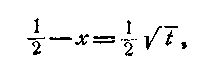
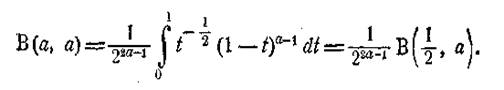то одержимо

Замінимо   в   обох   випадках   функцію   В   її   виразом  (12) через Г:

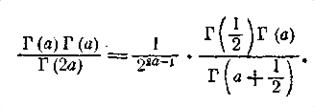
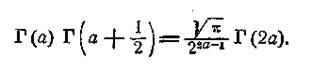Скорочуючи на  Г(а)  і  підставляючи замість   Г(1/2)   його   значення n (див. (14)], прийдемо до формули Лежандра:

Існує ще багато інших формул, що виявляють поглиблені властивості функції гамма. Ми не маємо можливості зупинятися тут на них, так само як і на способах наближеного обчислення значень самої функції гамма і її логарифма. Обмежимося згадуванням про те, що ще Лежандр, використовуючи властивості функції гамма и апарат нескінченних рядів, склав таблицю десяткових логарифмів Г (а) для а від 1 до 2 через 0,001, спочатку з 7, а потім з 12 десятковими знаками.

Нова, уже не елементарна, функція гамма є в такій же мірі освоєною нами, як і звичні нам функції, що ми назвали елементарними.

§ 6 Приклади.

Приведемо тепер кілька простих прикладів використання функції Г.

1) 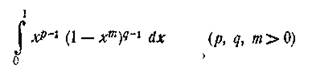 Інтеграл підстановкою х^т=у одразу зводиться до Ейлерового інтеграла першого роду:

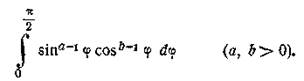
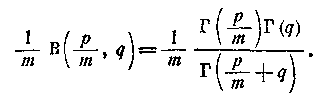2) Обчислимо інтеграл

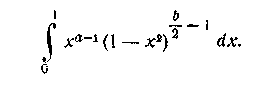Якщо покласти x = siny, то він зведеться до інтеграла

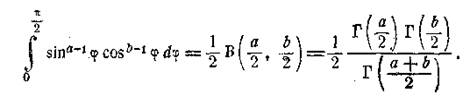Використовуючи попередній приклад, будемо мати

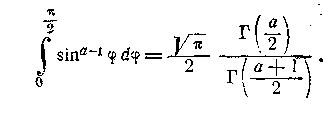Зокрема, при b=1, одержимо звідси

Легко   перевірити,   що   цією   однією   формулою   охоплюються й  обидві   формули (5) п° 187.

Якщо ж у вихідному інтегралі взяти а = 1 + с,   b=1- с,   де | с < 1, то знайдемо (застосовуючи формулу доповнення)

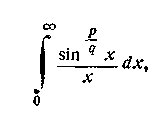3) Розглянемо, нарешті, ще інтеграл

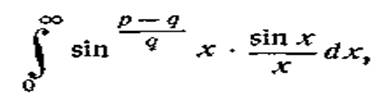де р и q — взаємно прості непарні натуральні числа. Переписавши інтеграл у виді

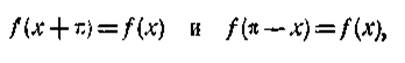застосуємо до нього  загальну  формулу  Лобачевского,  згадану на  стор. 135. Умови:

при яких ця формула вірна, для функції

 

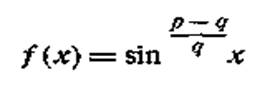виконані. У такий спосіб одержимо

З цих деяких прикладів  стає зрозумiлиим, наскільки, завдяки уведенню гамма функції, розширюються можливості представлення інтегралів у кінцевому вигляді через відомі функції. Інакше, навіть якщо гамма функція i не входить у кінцевий результат, одержання його полегшується з використанням властивостей цієї функції.