



5. Индексы средних уровней: индексы переменного, постоянного
состава и структурных сдвигов
В статистике часто приходится изучать динамику явлений, уровни которых представлены в виде средних величин (изменение средней заработной платы, средней себестоимости, средней цены и т.д.). В таких случаях необходимо выявить влияние на динамику средних показателей:
во-первых, изменения самих осредненных показателей;
во-вторых, изменение структуры изучаемого явления.
Например, средняя заработная плата на предприятии может вырасти за счет ее повышения у отдельных работников, а также за счет повышения удельного веса высокооплачиваемых категорий работников (например, с более высокими разрядами, т.е. в результате так называемого структурного сдвига).
Структурные сдвиги нередко являются причиной "статистических парадоксов", когда средние далеко выходят за пределы осредненных величин. Та же средняя заработная плата может возрасти больше, чем у отдельных работников, в связи с ростом удельного веса высокооплачиваемых категорий.
Влияние на динамику среднего уровня изучаемого явления отдельных факторов, т.е. изменение осредняемого показателя и изменение структуры, может быть изучено с помощью системы взаимосвязанных индексов.
Показатель динамики среднего показателя называется индексом переменного состава. Он равен произведению двух индексов: индекса осредняемого показателя в неизменной структуре, который называется индексом постоянного состава, на индекс структурных сдвигов.
Необходимо отметить, что все индексы качественных показателей (цены, себестоимости, производительности труда) являются индексами в неизменной структуре, или индексами постоянного состава. Они всегда сопоставляются с весами отчетного периода. Следовательно, чтобы построить систему индексов, индексы структурных сдвигов должны быть исчислены по весам базисного периода.
Рассмотрим построение этой системы на примере средней индекса цен.
Средняя цена единицы товара определяется по формуле средней арифметической взвешенной:
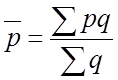 , где в качестве
весов используется количество товара.
, где в качестве
весов используется количество товара.
Следовательно, изменение средней цены можно выразить в виде индекса:
![]()
![]()
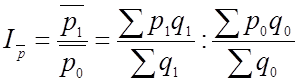 .
.
![]()
![]()
Этот индекс средней цены, рассчитанный как отношение двух средних с переменными весами, является индексом переменного состава и зависит от следующих факторов:
1). Изменение самих цен (например, если мы рассматривали овощи, то повысились цены на лук, капусту, картофель и т.д.). Это изменение выражается индексом постоянного состава, характеризующим изменение средней величины только за счет влияния индексируемых величин при постоянных весах:
![]()
![]()
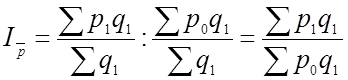 .
.
![]()
![]()
2). Структурные сдвиги в товарообороте а) изменение соотношений продаж по видам данного товара с различным уровнем цен (например, увеличиваются разновидности с более высокими ценами и уменьшаются с более дешевыми);
б) изменение соотношений продаж между организованным и неорганизованным рынками (например, увеличилась доля колхозного рынка, где цены выше, чем в магазинах);
в) изменение соотношений продаж по сезонам;
г) изменение соотношений продаж по поясам.
Влияние изменения структуры выражается индексом структурных сдвигов, который, как уже было сказано, взвешивается по весам базисного периода.
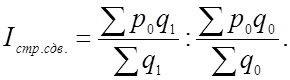
Этот индекс равен отношению индекса переменного состава к индексу постоянного состава.
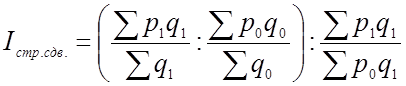 .
.
Так как может применяться не только количество реализованной продукции, но и удельный вес отдельных групп товаров, индекс структурных сдвигов может быть выражен в следующем виде:
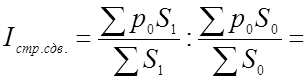
так как ![]() =100, то получим
=100, то получим
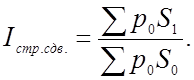
Взаимосвязь этих индексов в итоге можно выразить следующим образом:
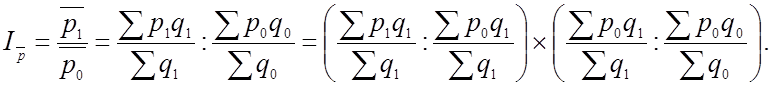
Iперем. состава Iпост. состава Iстр. сдв.
Изучение динамики средних показателей с помощью данной системы индексов возможно только после группировки данных изучаемой совокупности по признакам, характеризующим структурные сдвиги и вычисление групповых средних. Следовательно, этот индексный метод тесно связан с методом группировок.
Пример.
|
Товары |
Базисный период (сентябрь) |
Отчетный период (октябрь) |
Товарооборот |
||||
|
количество, кг q0 |
цена, млн.р. р0 |
количество, кг q1 |
цена, млн.р. р1 |
p0q0 |
p1q1 |
q1p0 |
|
|
1 |
50 |
5,0 |
40 |
4,5 |
250 |
180 |
200 |
|
2 |
50 |
6,0 |
70 |
6,5 |
300 |
455 |
420 |
|
Всего |
100 |
110 |
550 |
635 |
620 |
||
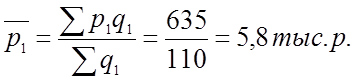
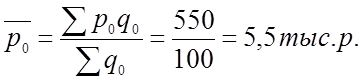
 или 105,5%. (переменного
состава)
или 105,5%. (переменного
состава)
Средняя цена на мед за месяц увеличилась на 5,5%, в т.ч. за счет:
а) изменения цен на рынках
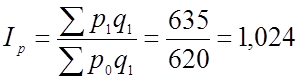 или 102,4%. (постоянного
состава)
или 102,4%. (постоянного
состава)
б) за счет изменения соотношения продаж между рынками:
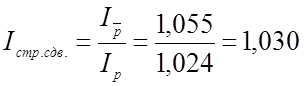 .
.
или
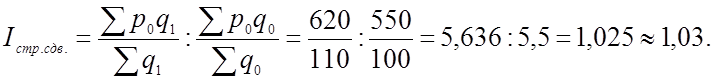
Индексы Ласпитреса — это индексы с базисными весами:
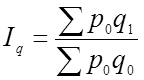 ;
; 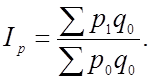
Индексы Пааше — это индексы с отчетными весами:
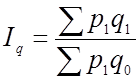 ;
; 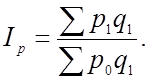
Идеальный индекс Фишера — это средняя геометрическая из произведения двух агрегатных индексов цен Пааше и Ласпитреса:
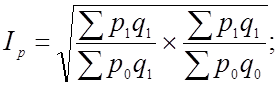
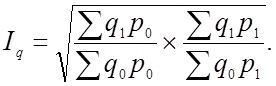
6. Взаимосвязь индексов и расчет на ее основе размера влияния
факторов на развитие сложных явлений
Индексный метод широко применяется для характеристики сложных общественных явлений, для оценки влияния на изменение этих явлений различных факторов, выступающих как множители общего результата. Оценка влияния различных факторов на изменение сложного явления может быть произведена путем построения системы взаимосвязанных индексов. При этом нужно иметь в виду, что взаимосвязь между индексами такая же, как и между абсолютными величинами.
Примеры:
1). Товарооборот = количество проданных товаров ´ цены
pq = p ´ q.
Соответственно взаимосвязь между индексами:
Ipq = Ip ´ Iq .
2). Выпуск продукции = среднесписочная численность работников ´ выработка одного работника
Iвып.пр. = Iч ´ Iпр.тр.
и т.д.
Если индекс произведения равен произведению индексов сомножителей, такие индексы являются сопряженными.
На изменение сложного явления могут оказывать влияние либо один, либо другой фактор, либо оба сразу. С экономической точки зрения небезразлично, за счет каких факторов произошло изменение явления, какой из них оказал решающее влияние.
Например, рост товарооборота, как показывает экономический анализ, по республике и в т.ч. по потребкооперации происходит только за счет роста цен. Физическая же масса товаров уменьшается.
Возьмем в качестве примера агрегатный индекс товарооборота
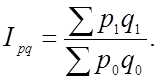
Исходя из того, что Ipq = Ip ´ Iq , тогда
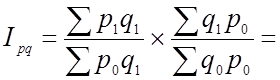 алгебраическим путем получаем
алгебраическим путем получаем 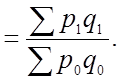
Таким образом, принцип построения системы индексов состоит в том, что для того, чтобы произведение сопряженных индексов было равно исходному показателю, необходимо веса этих сопряженных индексов брать на уровне разных периодов.
Если в данном примере индекс цен построен с количеством (весами) отчетного периода, то индекс количества построен с ценами (весами) базисного периода. При несоблюдении этого принципа системы взаимосвязанных индексов не получится.
Общее изменение сложного показателя (явления) представляет собой сумму изменений за счет влияния всех факторов. Если исследуется два фактора, повлиявших на изменение явления (например, товарооборот ↔ цены, количество товаров), то это будет двухфакторный анализ. Если факторов больше — то мы имеем либо многофакторную зависимость — трех-, четырехфакторную и т.д.
Прирост сложного показателя за счет качественного фактора (цена, производительность труда и т.д.) равняется приросту этого фактора, умноженному на отчетный уровень количественного фактора.
Прирост сложного показателя за счет количественного фактора (количество товаров, численность работников и т.д.) равен приросту этого фактора, умноженному на базисный уровень качественного фактора.
Пример: Дано:
|
Базисный период |
Отчетный период |
|
|
Численность работников, чел. |
30 |
35 |
|
Производительность труда, тыс.р. |
100 |
120 |
|
Общий выпуск, тыс.р. |
30 ´ 100 = 3000 |
35 ´ 120 = 4200 |
Решение:
Общий прирост выпуска = 4200 – 3000 = 1200 тыс.р., в т.ч. за счет:
а) прироста численности работников: (35-30) ´ 100 = 500 тыс.р.
б) прироста производительности труда: (120-100) ´ = 700 тыс.р.
Если известны 2 показателя, всегда можно найти третий.
При многофакторном анализе:
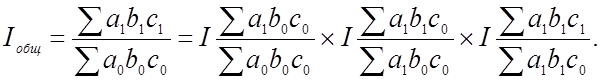
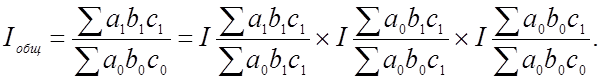
(сначала экстенсивные факторы, затем интенсивные — система взаимосвязанных индексов при трехфакторной модели)
В общем виде многофакторная связь выражается следующим образом:
1. Если взаимосвязь признаков начинается с экстенсивного фактора:
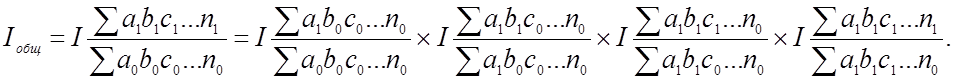
2. Если взаимосвязь признаков начинается с интенсивного фактора
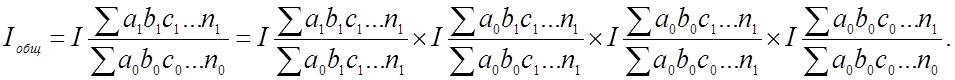
Вычитая из числителя каждого индекса его знаменатель, получим разложение общего абсолютного прироста результативного показателя на сумму абсолютных приростов влияния отдельных факторов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.