Модели технологических процессов и аппаратов, страница 4

6.  Коэффициенты теплопередачи принимаются неизменными по всей поверхности теплообменника;

7.  Потери тепла в окружающую среду не учитываются;

8.  Сечения и формы потоков постоянны. 

   Математическая модель теплообменника с полным смешением одного теплоносителя (количество F₁, температура Θ₁) и полным вытеснением другого (F₂, Θ₂) имеет вид:

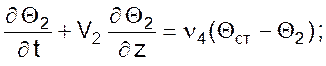
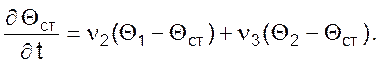
где

;

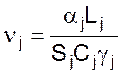V – скорость движения теплоносителя, м/с.

Математическая модель теплообменника с полным вытеснением обоих теплоносителей при условии, что тепловая емкость разделяющей стенки мала и может не учитываться имеет вид:

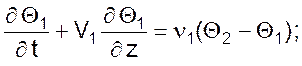
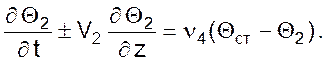
Математическая модель теплообменника с полным вытеснением обоих теплоносителей при условии, что тепловая емкость разделяющей стенки учитывается для противотока и прямотока, имеет вид:

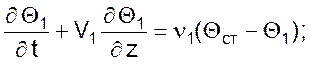
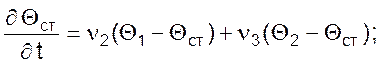
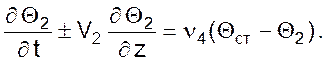
Математическая модель теплообменника с полным вытеснением обоих теплоносителей для перекрестного потока:

●   без учета тепловой емкости разделяющей стенки имеет вид:

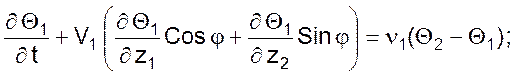
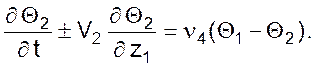
●  с учетом тепловой емкости разделяющей стенки имеет вид:

2.8.  Модель теплообменника с линейным распределением температур по его длине.

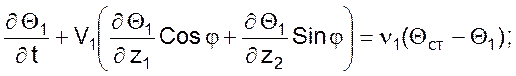
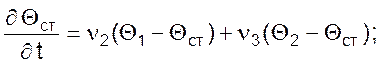
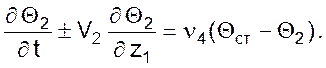
В этом случае кинетические и балансовые соотношения для противоточного теплообмена имеют вид:

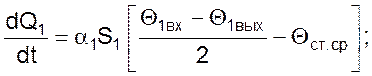
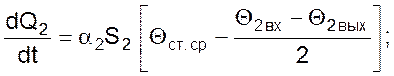
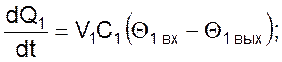
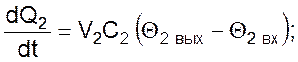
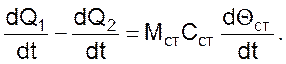
где   V – объемные расходы жидкостей, м³/с;

С – объемные теплоемкости жидкостей, Дж/(м³·К),

С_ст – массовая теплоемкость , Дж/(кг·К);

M_ст – масса стенки, кг.

Решив эту систему уравнений, можно получить, например, уравнение изменения температуры выходного потока во времени:

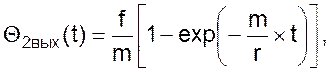
где

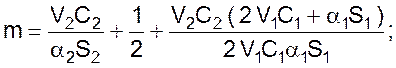
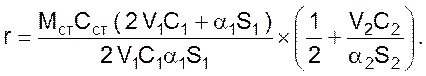
где  V – расход жидкости, кг/с;

С – теплоемкость, Дж/(кг·К);

α – коэффициент теплоотдачи, Вт/( м ²·К);

S – площадь поверхности теплоотдачи, м².

С приемлемой для практики точностью предложенные уравнения могут быть применены к расчету теплообменников, для которых отношение температур на входе и выходе меньше 2, что обычно и бывает на практике.

2.9.  Математические модели источников.

Под источником мы будем понимать элемент технологической схемы, из которого поток поступает в систему.

Рассмотрим один из наиболее распространенных источников - насос.

При расчетах моделью источника питания являются зависимости между напором H и расходом F и зависимость КПД hот расхода F.

Напор насоса представляет собой разность напоров, измеренных в узлах после насоса H_вых и перед ним H_вх:

Для центробежных насосов при фиксированном числе оборотов зависимость между напором и расходом имеет вид

С учетом числа оборотов двигателя n напор насоса H связан с подачей F уравнением вида:

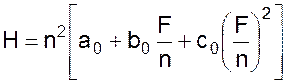
Коэффициенты в уравнениях берут из справочников, либо при необходимости точного их определения применяют методы статистической идентификации.

Зависимость КПД от расхода является рабочей характеристикой насоса и заносится в его паспорт. Аппроксимирующий полином этой зависимости имеет вид:

где h₀ – максимальный КПД;

F₀ – расход, соответствующий максимальному КПД;

b – эмпирический коэффициент.

2.9.1.    Модели гидравлических (пневматических) линий связи.

Гидравлические линии связи можно представить, как звенья чистого запаздывания при этом время запаздывания можно считать равным

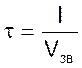, где     l – длина линии связи, м;

V_зв – скорость звука в жидкости, м/с.

В отличие от гидравлических аналитическое описание линий связи пневматических систем бывает, как правило, весьма и весьма сложным, что объясняется свойствами газа (способностью газа сжиматься под действием внешнего давления и изменениями его свойств при изменениях температуры). Поэтому уравнение неразрывности для газов справедливо лишь в форме, связывающей весовые - G₁, G₂  или массовые - M₁, M₂  расходы

2.10.  Модели трубопроводов.

2.10.1.    Модели стационарных режимов трубопроводов.

При движении жидкости по трубе напор уменьшается от H₁  в первом сечении до H₂ во втором. Разница между ними носит название потери напора и зависит от скорости движения жидкости v. Вид зависимости определяется шероховатостью трубы и режимом движения жидкости, который устанавливается по числу Рейнольдса

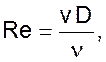
где D – диаметр трубопровода;

n - кинематический коэффициент вязкости рабочей жидкости.

При Re < 2500  движение ламинарное, свыше - турбулентное. При ламинарном движении потери напора пропорциональны скорости потока. При увеличении Re свыше 2500 сопротивление начинает быстро возрастать. При дальнейшем увеличением числа Re коэффициенты сопротивления (для определенной шероховатости) становится постоянными, не зависящими от Re. Эта область турбулентного движения жидкости называется областью автомодельной турбулентности.

В качестве модели участков гидравлических магистралей можно использовать зависимость потерь напора на трение и местные сопротивления на рассматриваемом участке гидросистемы от режима течения жидкости, свойств внутренней поверхности трубы, формы поперечного сечения, расхода жидкости и т.п.

Потери напора жидкости представляются функциями

где Q - параметры, характеризующие конструктивные свойства трубы.

На практике для расчета потерь напора инженеры используют целый ряд эмпирических формул Шевелева:

при v ³ 1.2 м/с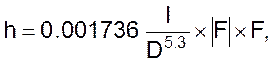  

при  v < 1.2 м/с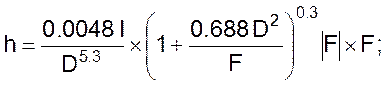 

Андрияшева

При   v < 3 м/с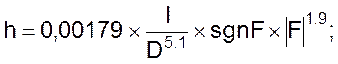  

Абрамова

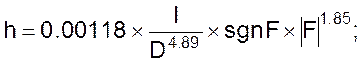
и др.

2.10.2.    Модели нестационарных режимов трубопроводов.

Примем, что на концах трубопровода имеются различные по величине гидродинамические напоры H, в результате чего в любом поперечном сечении трубопровода на жидкость в нем находящуюся действует давление P*

 

где S – площадь поперечного сечения трубопровода, м²;

r - удельный вес рабочего тела (жидкости), Н/м³.

Уравнение движения жидкости в трубопроводе имеет вид

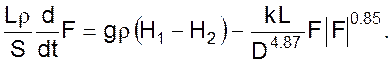
Как видно из уравнения расход F является функцией разности напоров H₁ и H₂, которые определяются из уравнения неразрывности струи:

Для входного сечения

 

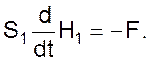
Для выходного сечения

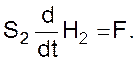
В совокупности представленные уравнения позволяют построить модель гидравлической системы, работающей в нестационарном режиме.

При моделировании гидравлических линий связи приходится учитывать местные сопротивления, например диафрагмы, задвижки и т.д. Потери напора на местных сопротивлениях можно представить в виде

 

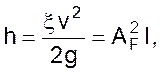
где x - коэффициент местного сопротивления;

A_F – удельное сопротивление трубы того же диаметра, что и местное сопротивление;

L = x/ 2gA_F – эквивалентная длина трубы.