Информатика и выч. техника \ Моделирование систем

Модели технологических процессов и аппаратов, страница 2

Предположим, что в аппарат поступает поток материала с объемным расходом q_вх. Тогда для установившегося режима можно записать

(01)

где q_вых и q_ап – объемные расходы выходного потока и потока внутри аппарата.

В общем случае в аппарате, который можно рассматривать как емкость, будет аккумулироваться некоторое количество компонента потока M

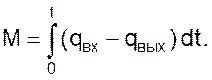(02)

Тогда концентрация вещества в аппарате с рабочим объемом V будет равна

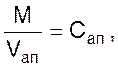по условию для аппарата идеального перемешивания

откуда

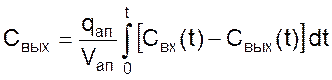(03)

Разрешим представленное уравнение относительно содержания компонента в процессе прохождения потока через аппарат

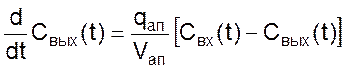(04)

или

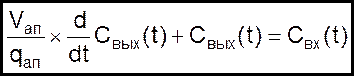(05)

Принимая

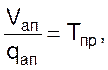(06)

запишем

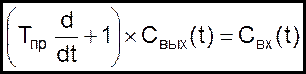(07)

Аналогичное по форме уравнение получим при рассмотрении изменения распределения температуры θ в потоке теплоносителя со структурой идеального перемешивания

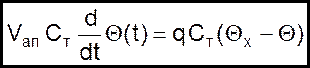(07)

где C_т – теплоемкость вещества потока теплоносителя;

θ – температура в любой точке идеального перемешивания (θ = θ_y);

θ_x – температура на входе в аппарат идеального перемешивания;

V_ап – объем аппарата;

q – объемный расход теплоносителя.

Передаточную функцию аппарата идеального смешения получим, преобразуя по Лапласу дифференциальное уравнение 05

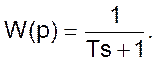(08)

Пример.

Рассмотрим случай, когда модель состоит из двух последовательно соединенных идеальных смесителей.

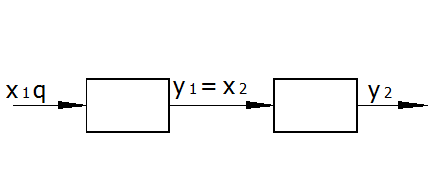
где x₁, y₁, x₂, y₂ - содержание контролируемого компонента в продукте;

q – объемный расход продукта.

Для первого смесителя можно записать

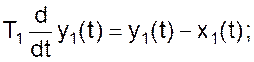
для второго

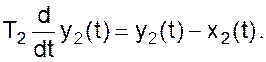
Здесь

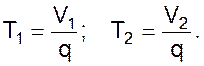
Содержание компонента в продукте, выходящем из первого смесителя, является входной величиной для второго смесителя y₁ = x₂.

Будем рассматривать аппараты как две последовательно соединенные емкости, в которых и происходит реакция, то есть как двух емкостную модель. Поскольку перемешивания вещества между емкостями не происходит, модель будем рассматривать как двух ячеечную. Решая систему уравнений для двух ячеечной модели, запишем

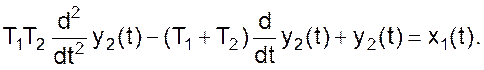
В более привычном виде уравнение, описывающее работу двух последовательно соединенных смесителей, может быть представлено в форме

2.2.2. Диффузионная модель.

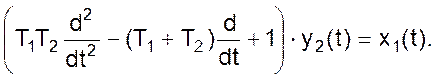
Диффузионная модель широко применяется при оценке реальных потоков в аппаратах, где происходит продольное перемешивание (потоки в слоях насадки). Различают однопараметрическую и двухпараметрическую диффузионные модели.

2.2.2.1. Однопараметрическая диффузионная модель.

Однопараметрической диффузионной моделью называют такую, которая учитывает только продольное перемешивание при этом единственным параметром, характеризующим однопараметрическую диффузионную модель, служит коэффициент продольного перемешивания D_L. В радиальном направлении распределение концентрации вещества принимается равномерное.

При составлении дифференциального уравнения однопараметрической диффузионной модели принимается:

● изменение содержания компонента потока является непрерывной функцией расстояния z;

● объемная производительность по потоку F не изменяется по длине и сечению потока;

● коэффициент продольного перемешивания D_L не изменяется по длине и сечению потока;

Уравнение диффузной модели при принятых допущениях имеет вид

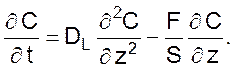
Из приведенного уравнения следует, что если D_L = 0 модель переходит в модель идеального вытеснения.

На практике коэффициент продольного перемешивания D_L вычисляется по эмпирическим расчетным формулам, составленным для аппаратов различных типов.

При экспериментальном определении D_L его обычно представляют в виде безразмерного комплекса. При этом используют критерий Пекле

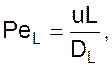
где L – определяющий линейный размер зоны перемешивания.

Коэффициент продольного перемешивания в безразмерной форме имеет вид

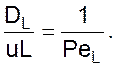
Правую часть полученного уравнения иногда называют обратным критерием Пекле. Он характеризует продольное перемешивание.

Если вместо средней скорости потока u подставить ее значение

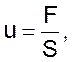
то уравнение, однопараметрической диффузионной модели, примет вид

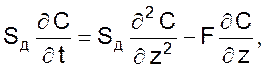
где S – площадь поперечного сечения потока.

2.2.2.2. Двухпараметрическая диффузионная модель.

Двухпараметрическая модель отличается тем, что она помимо продольного перемешивания учитывает и радиальное перемешивание. Для учета радиального перемешивания вводится второй параметр – коэффициент радиального перемешивания D_R. Такая модель более точно отражает процесс, но ее описание значительно усложняется, решение становится трудоемким и ввиду этого мало пригодным для практических целей. Двухпараметрические диффузионные модели разрабатываются, как правило, весьма редко и строго индивидуально для конкретных аппаратов.

2.3. Модели химических реакторов.

Реактор, как правило, соответствует простому элементу (с одним входным потоком), превращает определенную долю x_k выбранного ключевого реагента k (в соответствии с уравнением реакции с известными стехиометрическими коэффициентами) в конечный продукт.

Модель в этом случае представляется как

где A – матрица элементов вида

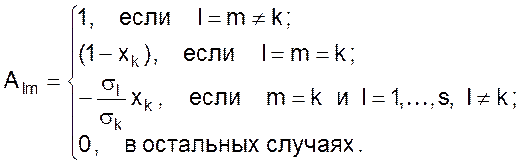
Здесь s_s – стехиометрический коэффициент s – го компонента в реакции при этом (s_s) > 0 для продуктов и (s_s) < 0 для реагентов.

Запись материальных балансов для реактора, включающего R реагентов, осуществляется при помощи R матриц преобразования: A⁽^r), r = 1, ¼, R.

Баланс компонентов может быть записан в обозначениях скоростей реакции r_r

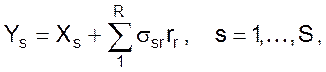
или в виде материального баланса продукта

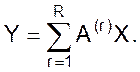
При последнем представлении предполагается, что реакции протекают последовательно, а не одновременно. Таким образом, степень превращения для каждой r-й реакции должна определяться на основе массового расхода гипотетического ключевого компонента после завершения (r – 1) реакции.

2.4. Смесительные модели.

2.4.1. Смесительная модель общего вида.

1 2 3 4

Скачать файл