При смесительной (соединительной) операции имеется n входных потоков и один выходной.
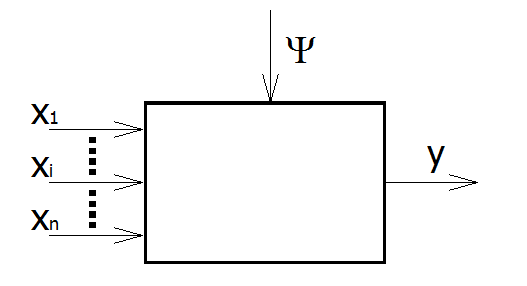
Рис. 1. Схема смесительной модели.
Общее уравнение операции
![]()
где xi – i –й входной поток;
Ψ (пси) - дополнительные факторы.
Конкретные модели отличаются видом функций f , которые, в общем случае, могут быть нелинейными.
Перейдем к рассмотрению смесительной модели линейного вида для чего введем переменные ui, определяющие соотношения, в которых смешиваются исходные потоки. Конкретный набор значений u1, ¼, un можно рассматривать как рецепт приготовления смеси. В этом случае модель будет иметь вид

Технологические операции разделения смесей осуществляются ректификацией, адсорбцией, сепарацией, флотацией и другими способами.
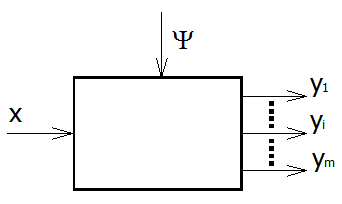
Рис. 1. Схема разделительной модели.
Общее уравнение разделительной операции может быть записано в виде
![]()
где yj – j –й выходной поток;
x – входной поток смеси;
Ψ(пси) - дополнительные факторы.
В частности, модель разделителя компонентов для случая разделения единичного входного потока x на m выходных потоков y в соответствии с долями разделения может быть представлена уравнением материального баланса в матричной форме:
![]()
В приведенном уравнении Y содержит s векторов соответствующих долей компонентов выходных потоков.
В массиве A диагональные элементы aj,s соответствуют доле s –го компонента во входном потоке, который является j в выходном потоке.
По условию aj,s = 0, если s –й компонент не присутствует в потоке. Таким образом, для всех s компонент, при которых xs ¹ 0, åaj,s = 1 то есть сумма концентраций всех компонентов равна единице.
Сложная модель описывает агрегат с n входными и m выходными потоками.
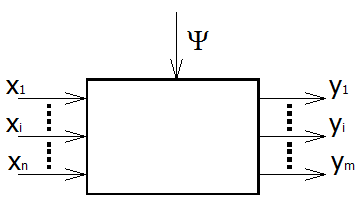
Рис. 3. Схема сложной модели.
В общем виде уравнение модели может быть представлено как
![]()
где yj – j –й выходной поток;
X – вектор компонентов входной смеси;
Ψ (пси) - дополнительные факторы.
Для такой модели функции fj можно представить в виде некоторых переменных коэффициентов, зависящих от Ψ (пси) и тогда уравнение модели примет вид
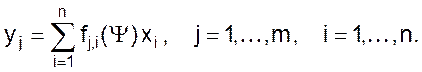
Полученная модель линейна относительно параметров материального потока. Управление потоком может производиться, как изменением коэффициентов fj,i, так и значений xi. Значения последних могут определяться запасом компонентов и возможными ограничениями на пропускную способность моделируемого агрегата.
Пример[1]
В качестве примера использования типовых элементарных моделей при моделировании промышленных объектов рассмотрим смесительный бак, который имеет постоянную площадь поперечного сечения S.
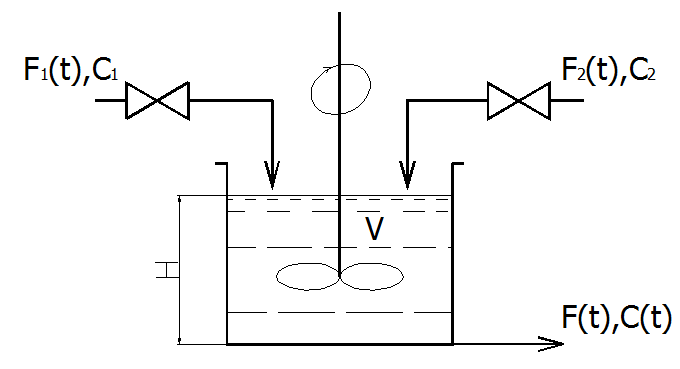
Бак наполняется с помощью двух потоков с расходами F1(t) и F2(t), причем концентрации контролируемого компонента C1 и C2 в потоках постоянны.
Перемешивание содержимого в баке идеально при этом концентрация контролируемого компонента C(t) в баке равна концентрации компонента на выходе из него (идеальное смешение).
Скорость изменения объема материала в баке
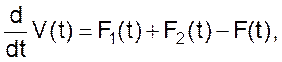
а скорость изменения концентрации
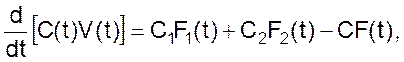
где V – объем жидкости в баке.
Мгновенный расход выходного потока F(t) зависит от высоты H:
![]()
где K – экспериментально определенная константа.
Учитывая, что площадь поперечного сечения бака S = Const, можно написать
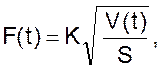
Подставляя расходы в уравнения скорости изменения объема и концентрации, получим
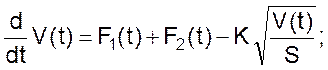
или
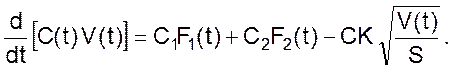
Таким образом, используя типовые схемы, мы составили математическую аналитическую модель смесительного бака.
Модели аппаратов химической технологии.
Реальные технологические аппараты представляют собой сложные много потоковые системы, в которых осуществляется переработка потоков сырья, полупродуктов, горючего теплоносителей и т.д. Для моделирования эти системы могут быть разбиты на подсистемы, каждая из которых выполняет в системе определенное законченное действие. Рассмотрим математические аналитические модели отдельных подсистем: теплообменников, источников, линий связи, трубопроводов.
Рассмотрим модели теплообмена для аппаратов с полным смешением одного или двух теплоносителей. В частности теплообменник с полным вытеснением одного и полным смешением другого теплоносителя (змеевик, расположенный в баке, представлен на рис. 1).
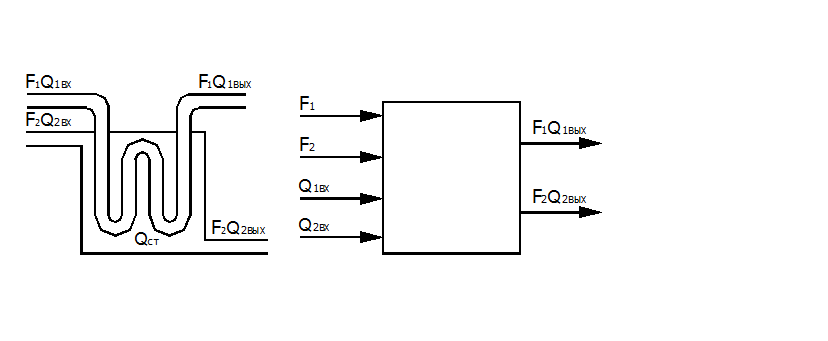
Рис. 1. Теплообменник.
Основные переменные процесса переноса тепла в теплообменниках связаны уравнениями теплового баланса и имеют вид:
Для двух теплоносителей:
![]()
Для горячего теплоносителя:
![]()
Для холодного теплоносителя:
![]()
Здесь и на рисунке приняты следующие обозначения:
C – удельная теплоемкость, кДж/(кг·К);
F – расход, кг/с;
Q – количество тепла, кДж;
Θ – температура, °К;
S – площадь поверхности теплоотдачи, м²;
a - коэффициент теплоотдачи, Вт/(м²·К);
g - удельный вес, Н/м³;
l - коэффициент теплопроводности, Вт/(м·К);
d - толщина стенки, м.
Обозначение индексов:
ст – стенка разделяющая;
ср – средняя температура;
пот – потери;
1, 2 – горячий и холодный соответственно.
Схема теплопередачи через стенку приведена на рис. 2.
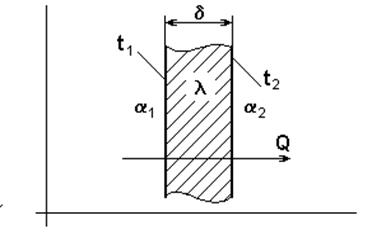 |
Рис. 2 Схема теплопередачи через стенку.
Уравнение теплопередачи имеет вид
![]() ,
,
где коэффициент теплопередачи
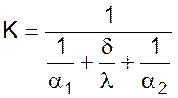
Величина, обратная коэффициенту теплопередачи носит название термического сопротивления и состоит из:
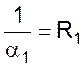 - термического
сопротивления теплоотдачи от греющей жидкости к поверхности стенки;
- термического
сопротивления теплоотдачи от греющей жидкости к поверхности стенки;
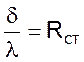 - термического
сопротивления теплопроводности стенки;
- термического
сопротивления теплопроводности стенки;
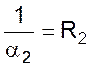 - термическое
сопротивление от поверхности стенки к нагреваемой жидкости.
- термическое
сопротивление от поверхности стенки к нагреваемой жидкости.
Следует отметить, что тепловой баланс не является уравнением связи (по нему, например, нельзя непосредственно определить температуру на выходе теплообменника).
Для написания математической модели необходимо принять ряд допущений:
1. Одна из жидкостей движется в теплообменнике внутри трубы, которая омывается другой жидкостью;
2. Обе жидкости движутся в одном направлении по оси z;
3. В направлении, перпендикулярном к направлению движения теплоносителей, смешение полное, потому скорости и температуры их в любой плоскости, перпендикулярной к оси z, усредняются;
4. Смешение теплоносителей и передача тепла в стенке трубы в направлении движения сред не учитываются;
5. Удельные теплоемкости и плотности жидкостей, в области рассматриваемых температур, принимаются постоянными;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.