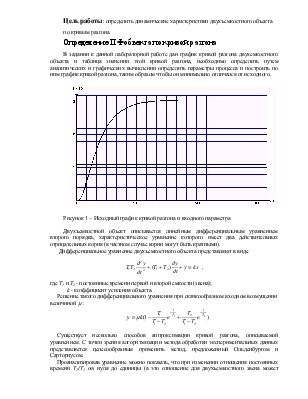



В задании к данной лабораторной работе дан график кривой разгона двухемкостного объекта и таблица значении этой кривой разгона, необходимо определить путем аналитических и графических вычислении определить параметры процесса и построить по ним график кривой разгона, таким образом чтобы он минимально отличался от исходного.
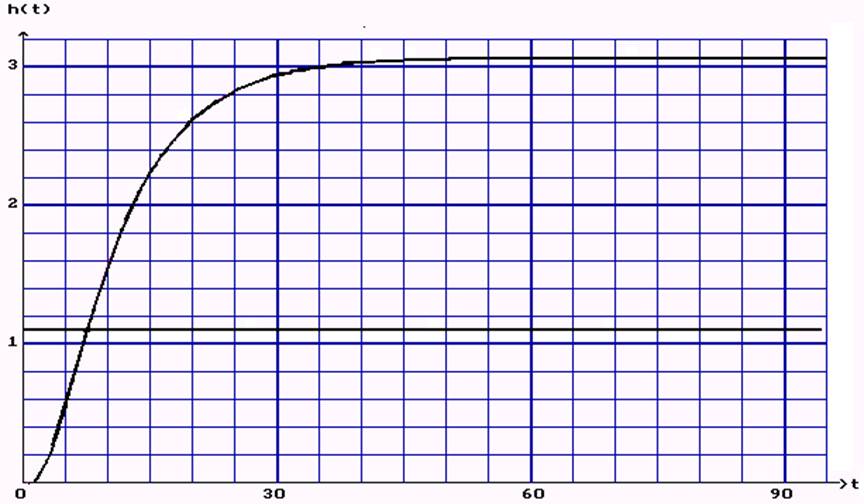
Рисунок 1 – Исходный график кривой разгона и входного параметра
Двухъемкостной объект описывается линейным дифференциальным уравнением второго порядка, характеристическое уравнение которого имеет два действительных отрицательных корня (в частном случае корни могут быть кратными).
Дифференциальное уравнение двухъемкостного объекта представляют в виде
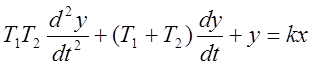 ,
,
где T1 и T2 - постоянные времени первой и второй емкости (звена);
k - коэффициент усиления объекта.
Решение
такого дифференциального уравнения при скачкообразном входном возмущении
величиной ![]() :
:
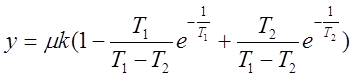
Существует несколько способов аппроксимации кривой разгона, описываемой уравнением. С точки зрения алгоритмизации метода обработки экспериментальных данных представляется целесообразным применить метод, предложенный Ольденбургом и Сарториусом.
Проанализировав уравнение можно показать, что при изменении отнощения постоянных времени T2/T1 от нуля до единицы (а это отношение для двухъемкостного звена может меняться только в этих пределах) отношение b/a (рисунок 1) меняется от единицы до 0,7357.
Зависимость b/a от T2/T1 выражается формулой
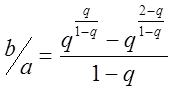
На основании формулы построен график зависимости отношений T2/T1 и b/a (рисунок 2).
|
|
|
|
Рисунок 2 - Обработка кривой разгона Рисунок 3- Номограмма для определения
апериодического объекта второго T2/T1 по b/a
порядка
Из
формулы следует, что при отношениях b/a, полученных с реальной кривой разгона, больших 0,83,
объект может быть представлен как одноемкостный (с запаздыванием), поскольку
отношение T2/T1 в этом случае меньше 0,15, т. е. T2, составляет
меньше 15% от T1. Кроме
того, при отношениях b/a, меньших
0,7357, объект не является двухъемкостным, а описывается дифференциальным
уравнением более высокого порядка. Отсюда, в частности, можно получить
критерий для машинного, определения порядка дифференциального уравнения,
описывающего объект:
b/a >0,83—одноемкостный объект;
0,7357![]() b/a
b/a ![]() 0,83 —
двухъемкостный объект;
0,83 —
двухъемкостный объект;
b/a <0,7357— трехъемкостный объект или объект более высокого .порядка.
Прежде всего, необходимо отыскать точку перегиба на кривой разгона. Тангенс угла наклона касательной можно определить
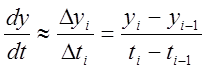
Имея в виду, что шаг замеров постоянный ![]() , определим точку перегиба как
точку, в которой
, определим точку перегиба как
точку, в которой ![]() . На реальных
кривых точка перегиба обычно не выражена достаточно четко. Поэтому несколько
значений
. На реальных
кривых точка перегиба обычно не выражена достаточно четко. Поэтому несколько
значений ![]() в средней части кривой могут иметь равные или близкие значения.
Выберем точки, в которых приращения функции отличаются не более чем на 1 %, т.
е.
в средней части кривой могут иметь равные или близкие значения.
Выберем точки, в которых приращения функции отличаются не более чем на 1 %, т.
е.
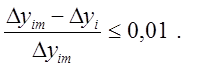
В средней части кривой неравенству будут удовлетворять несколько точек, которые определяем из таблицы значении представленной в программе:
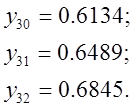
Проведем
через них прямую у =
mt + с, которая
будет являться касательной к кривой разгона в точке перегиба. Коэффициенты
найдем по методу наименьших квадратов.
Для этого потребуется, чтобы:
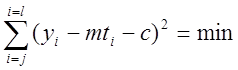
Взяв частные производные суммы по m и с и приравняв их нулю, получим систему из двух уравнений с двумя неизвестными, решив которую, получим
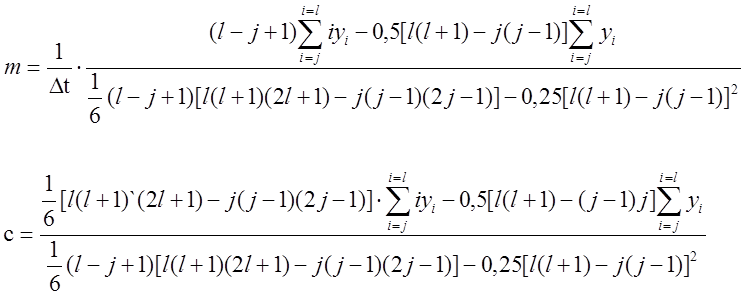
где l =32;
j =30;
yi – значения точек перегиба.
Подставляем численные данные в формулы:
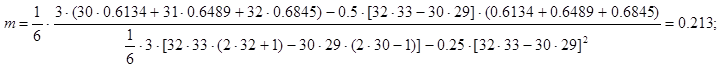
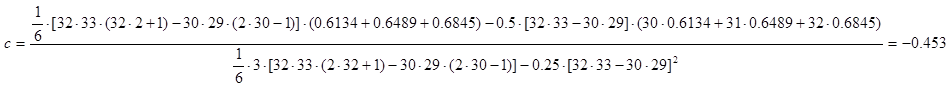
Определим координаты точек пересечения касательной с осью абсцисс и асимптотой из уравнений
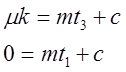
где ![]() — отрезок, отсекаемый на оси ординат асимптотой,
значение, которого определяем по исходному графику.
— отрезок, отсекаемый на оси ординат асимптотой,
значение, которого определяем по исходному графику.
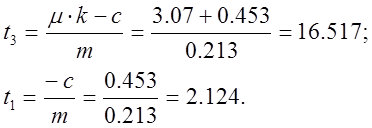
Абсциссу точки перегиба интерполяцией по формуле:
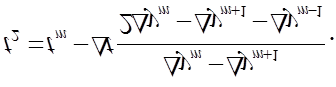
![]()
Вычислив значения t1, t2 и t3 , получим
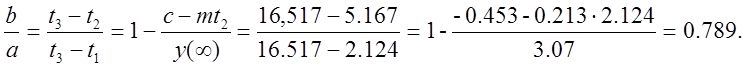
Аппроксимировав кривую на рисунке 3, получим зависимость Т2/Т2 от b/a:
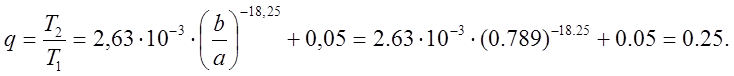
Имея в виду, что 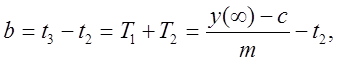
Можем составить систему из двух уравнений относительно неизвестных Т1 и Т2 решив которую , получим
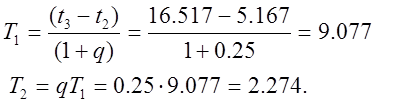
После определения постоянных времени, определяем недостающие параметры двухемкостного объекта определяем из кривой разгона, которая представлена в программе:
![]() - численное
значение установившегося значения выходной величины;
- численное
значение установившегося значения выходной величины;
![]() - величина скачка
входного параметра;
- величина скачка
входного параметра;
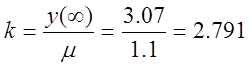 - коэффициент
усиления;
- коэффициент
усиления;
![]() - время запаздывания определяемый по исходному графику.
- время запаздывания определяемый по исходному графику.
Зная параметры двухемкостного объекта можно определить передаточную характеристику данного объекта, передаточная функция будет иметь следующий вид:
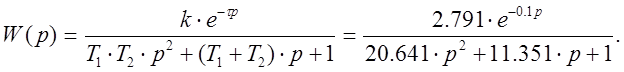
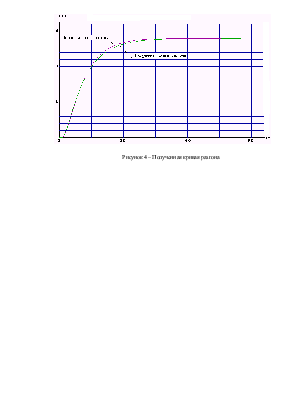
Подставляя полученные данные в программу получаем график переходного процесса двухемкостного объекта.
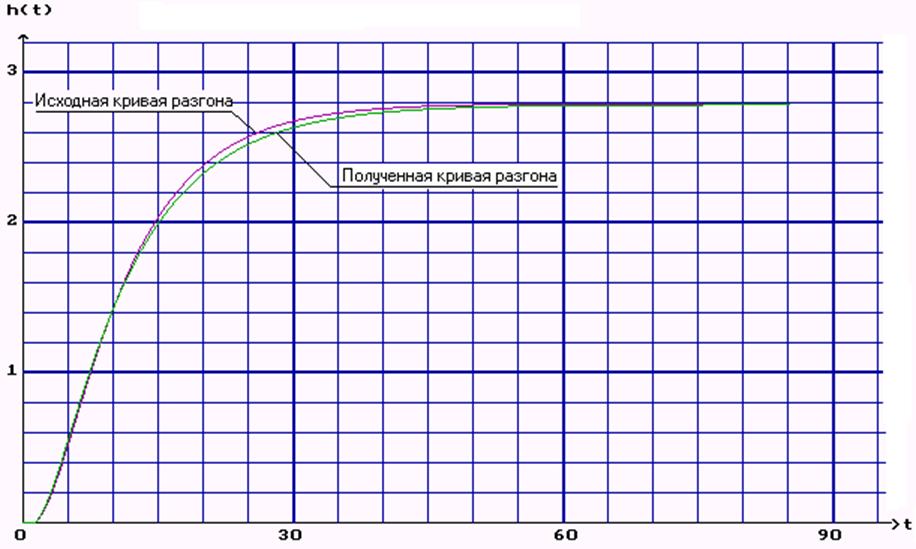
Рисунок 4 – Полученная кривая разгона
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.