Расчет одноконтурных систем автоматического регулирования, страница 4

            σ

  t

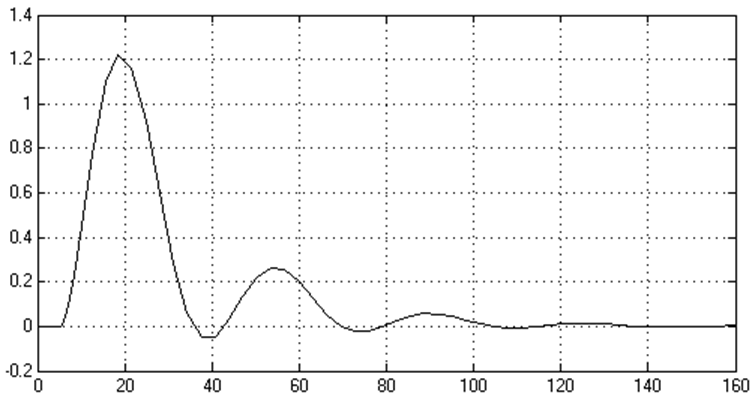
Рисунок 2.6 - График процесса регулирования САР (точка 5)

            σ

  t

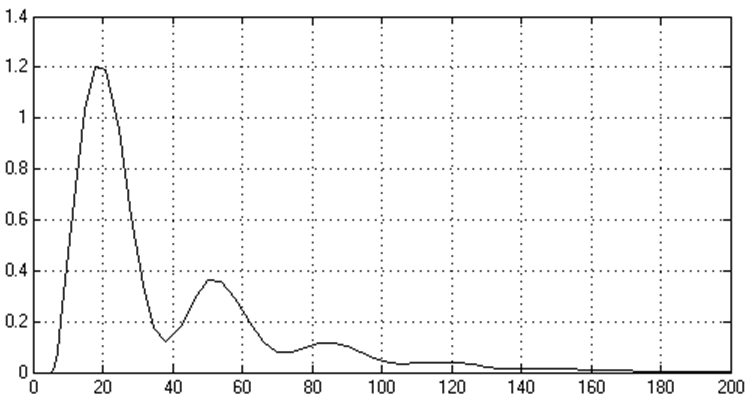
Рисунок 2.7 - График процесса регулирования САР (точка 6)

2.2 Расчет параметров настройки ПИД-регулятора методом незатухающих колебаний

В соответствии с этим методом, расчёт настроек ПИД-регулятора проводится в два этапа:

1)  расчёт критической настройки пропорциональной составляющей

(C₀ = С₂ = 0), при которой АСР будет находится на границе устойчивости, и соответствующее ей :

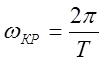;                                                     (2.9)

     2) определение по  и  оптимальных настроек (,,) регулятора, обеспечивающих степень затухания .

Так как интегрирующая и дифференциальная составляющие из условия расчёта равны нулю (C₀ = С₂ = 0), следовательно, при помощи пакета MATLAB подбираем пропорциональную составляющую .

       σ  

     t

Рисунок 2.8 – Автоколебательный процесс

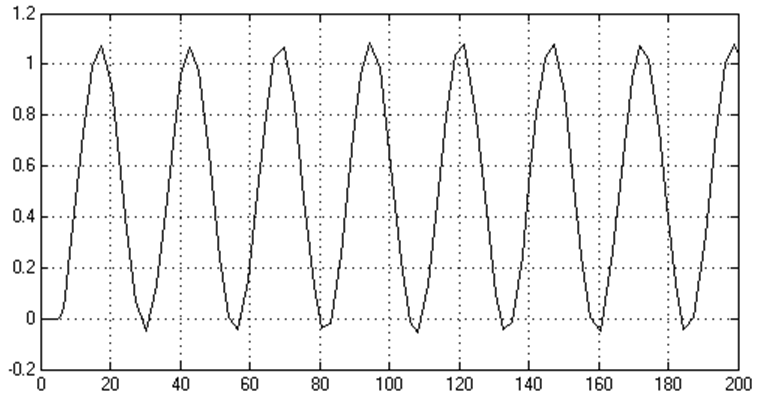
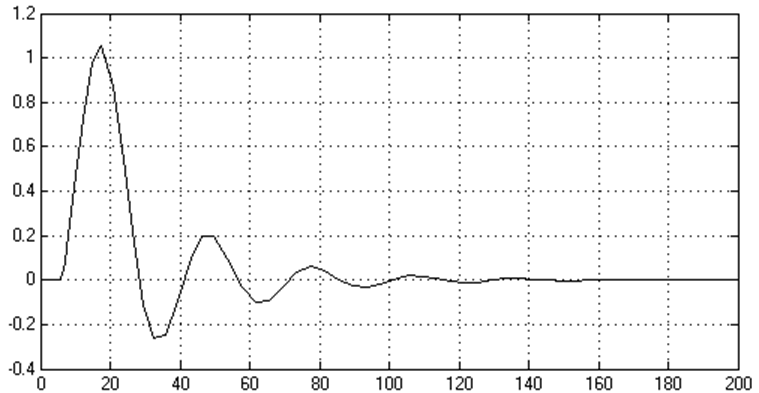
Из рисунка 2.8 видно, что период автоколебаний, при котором АСР находится на границе устойчивости, равен: T = 24 мин.                             

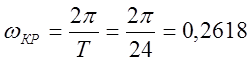 рад/мин.

Оптимальные настройки ПИД-регулятора находим по следующим формулам:

; ; .                (2.10)

                                         ;              

;

.

                σ

   t

Рисунок 2.9 –Процесс регулирования с оптимальными

настройками ПИД-регулятора

3 Анализ качества настройки ПИ-регулятора

Анализ процессов, соответствующих различным значениям С₀ и С₁, лежащим на кривой равной степени затухания (рисунок 2.1), показывает, что качество переходного процесса при заданной степени затухания  изменяется в зависимости от выбранных значений С₀ и С₁.

Оптимальный переходный процесс должен удовлетворять следующим критериям качества:

- затухание переходного процесса должно быть интенсивным (Y=0,75¸0,9);

- максимальное отклонение регулируемой величины должно быть наименьшим (y_max=min);

- продолжительность переходного процесса должно быть минимальным

        (t_p­=min);

- интегральный квадратичный критерий 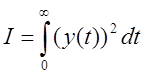должен быть минимальным;

Таблица 3.1 – Критерии качества для выбранных точек кривой равной степени затухания ПИ-регулятора

Параметры точки кривой равной степени затухания	Степень затухания, Y	Максимальное отклонение,  ymax	Время регулирования, tp	Интегральный квадратичный критерий,  *
Точка 1 w=0.0560           С0=0.0102 С1=-0.0591 Рисунок 2.2	0,75	2,058	410	0,5148
Точка 2 w= 0.0860 С0=0.0200 С1=0.0502 Рисунок 2.3	0,75	1,569	286	0,3185
Точка 3 w=0.1320 С0=0.03 С1=0.2197 Рисунок 2.4	0,75	1,307	205	0,2183
Точка 4 w= 0.1710 С0=0.0252 С1=0.3374 Рисунок 2.5	0,75	1,236	142	0,1816
Точка 5 w= 0.1830 С0=0.0201 С1=0.3649 Рисунок 2.6	0,75	1,226	134	0,1813
Точка 6 w= 0.1920 С0=0.0150 С1=0.3823 Рисунок 2.7	0,75	1,223	172	0,1893

*-Значения интегрального квадратичного критерия получены с помощью пакета

   Matlab

Из таблицы 3.1 видим, что наилучшими критериями качества процесс обладает при настройках ПИ-регулятора соответствующих точке 5 на кривой равной степени затухания, т.е. интегральный квадратичный критерий имеет наименьшее значение (), и минимальное значение времени регулирования (),а так же сравнительно не большое максимальное отклонение ().

Так если двигаться по кривой от меньших значений частоты к большей (таблица 2.1), то амплитуды колебаний регулируемой величины уменьшаются (рисунки 2.2, 2.3, 2.4, 2.5, 2.6, 2.7), однако по мере приближения к оси абсцисс процесс затягивается, а при значении С₀ лежащем на оси абсцисс он характеризуется наименьшим отклонением регулируемой величины и остаточной неравномерностью.

Многочисленные промышленные опыты настройки регуляторов показывают, что следует выбирать С₀ и С₁ (рисунок 2.6) лежащие несколько правее максимума кривой заданного затухания (точка 5 рисунок 2.1).

В данной курсовой работе наиболее благоприятными переходным процессом являются процесс при следующих настройках ПИ-регулятора:

для  ПИ-регулятора С₀ = 0,0201 и С₁ = 0,3649.

Заключение

В соответствии с заданием на курсовое проектирование по кривой разгона определены динамические характеристики объекта регулирования (передаточная функция, переходная характеристика, весовая характеристика, ЛАЧХ, ЛФЧХ, АФЧХ, расположение на комплексной плоскости нулей и единиц).

В данной курсовой работе определена передаточная характеристика объекта регулирования по кривой разгона. Приведены расчёты параметров настройки ПИ-регулятора методом расширенных частотных характеристик и расчет ПИД-регулятора методом незатухающих колебаний, построен график оптимального переходного процесса регулирования.

В данной курсовой работе наиболее благоприятными переходными процессами являются процессы при следующих настройках регуляторов:

для  ПИ-регулятора С₀ = 0,0201 и С₁ = 0,3649;

для  ПИД-регулятора С₁ = 0,4601604 , С₀ = 0,0385504 и С₂ = 1,379778.

Список используемых источников

1. Филин В.А. Расчёт локальных систем автоматического управления: Учебное    пособие для студентов специальности 0639. Красноярск, КГУ: 1981,99с.

2. Автоматическое управление в химической промышленности: Учебник для вузов. Под ред. Е.Г. Дудникова. – М.: Химия, 1987. – 368 с.