Расчет одноконтурных систем автоматического регулирования, страница 2

Реферат

В данном курсовом проекте приведены динамические характеристики объекта регулирования (передаточная функция, переходная характеристика, весовая характеристика, ЛАЧХ, ЛФЧХ, АФЧХ, расположение на комплексной плоскости нулей и единиц). Представлены результаты расчётов параметров настройки ПИ-регулятора методом расширенных частотных характеристик (РЧХ) и параметров настройки ПИД-регулятора методом незатухающих колебаний с соответствующими графиками процесса регулирования, а так же анализ качества настройки регулятора.

Курсовой проект содержит пояснительную записку из 24 страниц текста, 3 таблиц, 15 рисунков и 2 литературных источника.

Содержание

Введение… … … …………………………………………………………………....5

1 Определение динамических характеристик объекта регулирования

по кривой разгона………………………………………………………… …… …..6

2 Расчёт настроек ПИ- и ПИД- регуляторов в одноконтурных АСР ……….11

 2.1 Расчет параметров настройки ПИ-регулятора методом

 расширенных частотных характеристик ……………………………………. .11

 2.2 Расчет параметров настройки ПИД-регулятора методом

 незатухающих колебаний ……………………………………………………….16

3 Анализ качества настройки ПИ-регулятора…………………………………..18

Заключение … … ………………………………………………………………….. 19

Список используемых источников …………………………………………….....20

Введение

Возрастающие требования к качеству ведения технологического процесса обуславливает широкое внедрение систем автоматического регулирования различной степени сложности. Важное место среди них занимают системы локальной автоматики. Однако, как показывает практика их эксплуатации, эффективности внедрения таких систем в значительной мере определяется качеством их наладки и степенью оптимальности выбранных параметров настройки регуляторов.

Несмотря на все возрастающие масштабы внедрения автоматизированных систем управления технологическими процессами (АСУ ТП) роль и значение локальных систем регулирования нисколько не уменьшается. Зачастую являясь составной частью такой системы, они определяют её надёжность, гибкость, «живучесть».

Под локальной автоматической системой регулирования (ЛАСР) понимают систему, которая выполняет задачи автоматического регулирования технологического(их) параметра(ов) с помощью традиционных общепромышленных средств автоматизации. Элементы такой системы могут устанавливаются либо непосредственно на объекте, либо быть удалёнными от него в специальное диспетчерское (централизованное) помещение.

Любая система автоматического регулирования включает в себя набор определённых элементов, динамически связанных между собой. К ним относятся:

·  объект управления (регулирования);

·  датчик (преобразователь), возможно совместно с усилителем;

·  регулятор (возможно с элементом сравнения);

·  исполнительное устройство;

·  регулирующий орган.

При расчёте подобной системы автоматического регулирования приходится иметь дело с двумя видами задач.

Первая задача.

При выбранных элементах системы регулирования (уже смонтированных на месте) определить и установить такие значения параметров настройки регулятора (коэффициенты передачи регулятора, времени изодрона, времени предварения и т.д.), которые бы обеспечивали требуемое качество работы системы в процессе её эксплуатации.

Вторая задача.

Решается на стадии разработки проектирования САР. Её сущность заключается в том, что при заданном объекте управления и поставленными требованиями к качеству управления, подобрать такие элементы системы, включая регулятор, диапазон изменения настроенных параметров которых обеспечивало выполнение эти условий при некотором изменении нагрузки.

Решение первой задачи сводится к динамической настройке автоматического регулятора, входящего в систему.

Под динамической настройкой динамического регулятора понимается определение и установка конкретных значений параметров настройки (коэффициенты передачи регулятора, времени изодрона, времени предварения), обеспечивающих требуемое качество работы САР.

1 Определение динамических характеристик объекта регулирования по кривой разгона

Двухёмкосный объект описывается линейным дифференциальным уравнением второго порядка (1.1), характеристическое уравнение которого имеет два действительных отрицательных корня (в частной случае корни могут быть кратными).

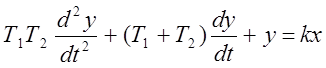,                                    (1.1)

где Т₁ и Т₂ – постоянные времени первой и второй ёмкости (звена);

k – коэффициент усиления объекта.

Прежде всего, необходимо отыскать точку перегиба на кривой разгона. Тангенс угла наклона касательной можно определить из следующего отношения:

.                                            (1.2)

Имея в виду, что шаг замеров постоянный , определим точку перегиба как точку, в которой .

На реальных кривых точка перегиба обычно не выражена достаточно четко. Поэтому несколько значений  в средней части кривой могут иметь равные или близкие значения. Выберем точки, в которых приращения функции отличаются не более чем на 1 %, т. е.

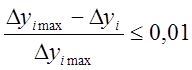 .                                          (1.3)

В средней части кривой разгона неравенству будут удовлетворять несколько точек  (таблица 1.1). Проведем через них прямую у = mt + с, которая будет являться касательной к кривой разгона в точке перегиба.

Таблица 1.1 – Точки кривой разгона

 удовлетворяющие условию (1.3)

			£ 1%
61	0,4977	0,0223	0,45
62	0,5200
		0,0223	0,45
63	0,5423
		0,0224	0,0
64	0,5647
		0,0223	0,45
65	0,5870