Коэффициенты находим по методу наименьших квадратов. Для этого необходимо, чтобы:
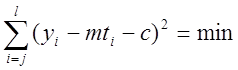 . (1.4)
. (1.4)
Взяв частные производные и приняв их равными нулю, получим систему из двух уравнений с двумя неизвестными, решив которую получаем следующее:
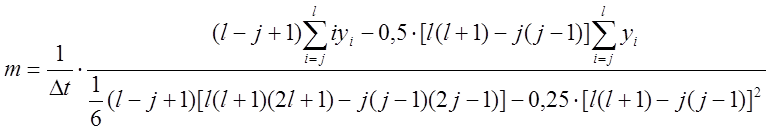 ; (1.5)
; (1.5)
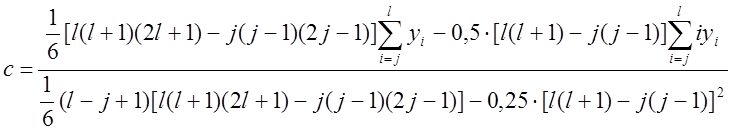 . (1.6)
. (1.6)
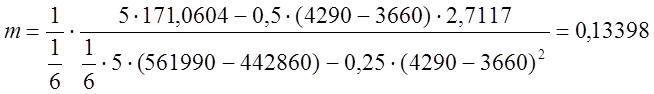 ;
;
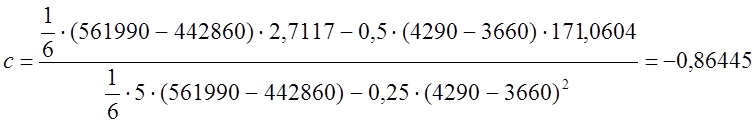 .
.
Уравнение касательной
![]() имеет вид:
имеет вид: ![]() .
.
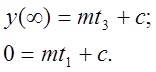 (1.7)
(1.7)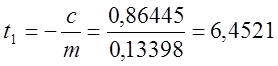 ;
; 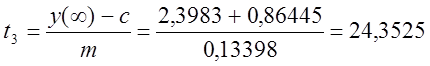 ;
;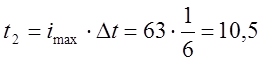 ;
(1.8)
;
(1.8)
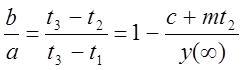 ; (1.9)
; (1.9)
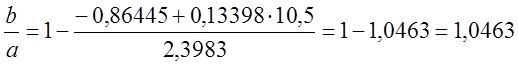 .
.
Аппроксимируя
зависимость ![]() от
от ![]() получаем:
получаем:
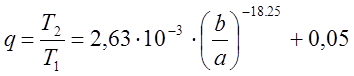 ; (1.10)
; (1.10)
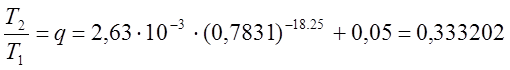 .
.
Из (1.9) видно, что 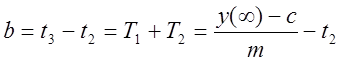 , следовательно, составляем систему из двух
уравнений относительно неизвестных Т1 и Т2,
решив которые получаем:
, следовательно, составляем систему из двух
уравнений относительно неизвестных Т1 и Т2,
решив которые получаем:
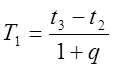 ,
, ![]() . (1.11)
. (1.11)
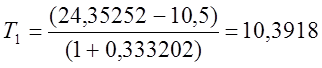 ;
; ![]() .
.
Недостающие параметры двухёмкостного объекта определяем из кривой разгона:
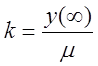 , (1.12)
, (1.12)
где ![]() -
коэффициент усиления;
-
коэффициент усиления;
y![]() = 2,2486 – численное значение
отрезка, отсекаемого на оси ординат асимптотой к кривой разгона;
= 2,2486 – численное значение
отрезка, отсекаемого на оси ординат асимптотой к кривой разгона;
![]() – величина скачка входного
параметра.
– величина скачка входного
параметра.
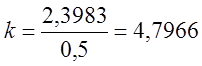 .
.
Зная параметры двухёмкостного
объекта, определяем передаточные характеристики данного объекта, передаточная
функция будет иметь следующий вид (где ![]() ):
):
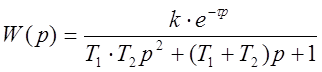 ; (1.13)
; (1.13)
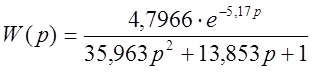 .
.
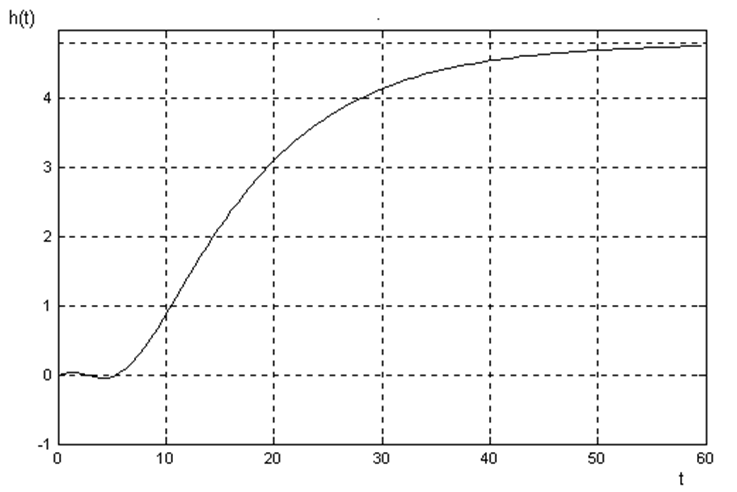
Рисунок 1.1 – Переходная (разгонная) характеристика
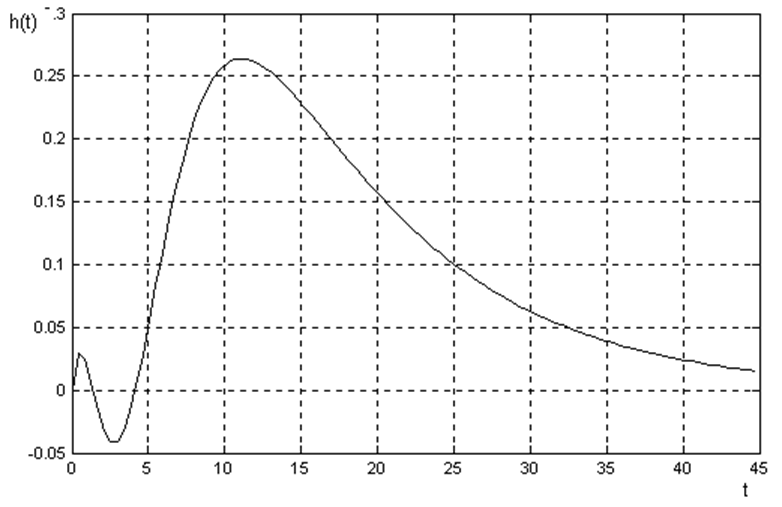
Рисунок 1.2 – Весовая характеристика
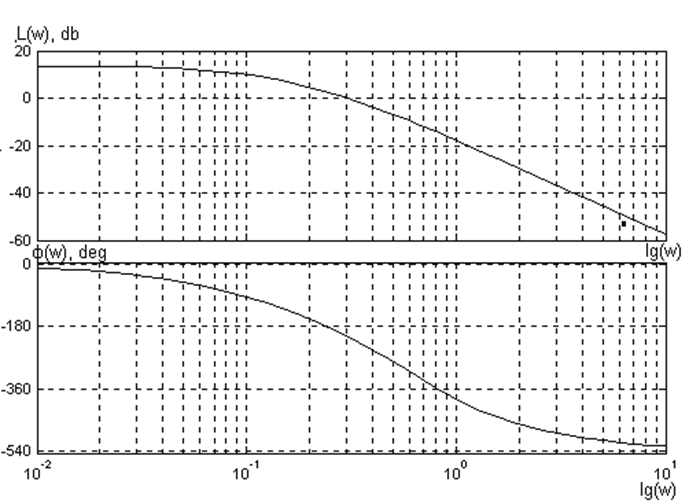
Рисунок 1.3 – ЛАЧХ и ЛФЧХ
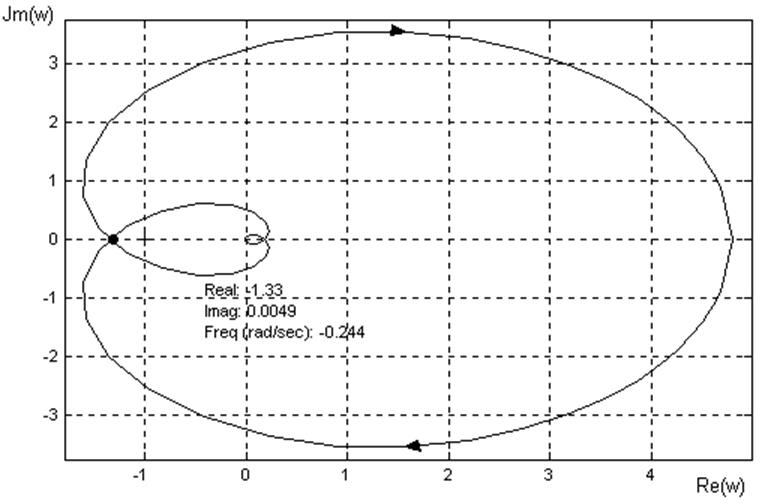
Рисунок 1.4 – Годограф Найквиста
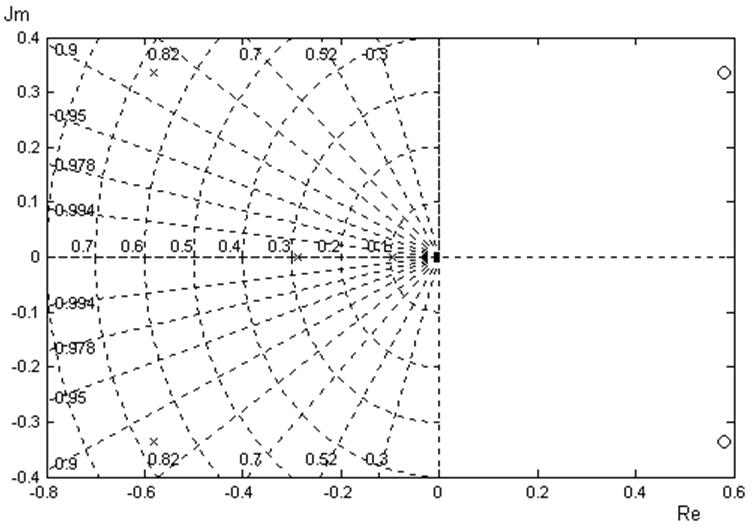
Рисунок 1.5 – Расположение на комплексной плоскости нулей и единиц
2 Расчёт настроек ПИ- и ПИД- регуляторов в одноконтурных АСР
2.1 Расчёт параметров настройки ПИ-регулятора методом расширенных частотных характеристик
Выражения
передаточных функций W(p) звеньев или систем
регулирования, для которых наложено ограничение ![]() ,
называются расширенными амплитудно-фазными характеристиками и обозначаются
,
называются расширенными амплитудно-фазными характеристиками и обозначаются ![]() .
.
Таким образом, для расчёта системы регулирования на заданную степень затухания необходимо располагать расширенными амплитудно-фазными характеристиками объекта и регулятора. Так же, как и при расчёте устойчивости исходным условием является соотношение:
![]() . (2.1)
. (2.1)
Итак, с помощью расширенных частотных характеристик можно рассчитать систему регулирования на заданную степень затухания, то есть построить в плоскости параметров настройки регулятора линию равной степени затухания или колебательности.
Степень колебательности берём (по заданию) равной: ![]() .
.
![]() , (2.2)
, (2.2)
где 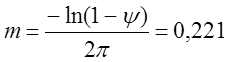 .
.
Чтобы построить расширенные частотные характеристики необходимо оператор р заменить и подставить в рассчитанную ранее передаточную функцию (1.13):
![]() , где
, где ![]() ; (2.3)
; (2.3)
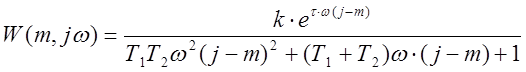 ; (2.4)
; (2.4)
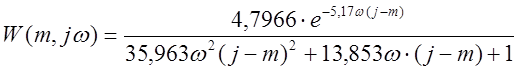 ;
;
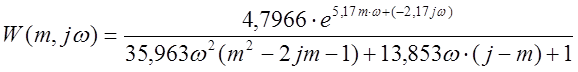 ;
;
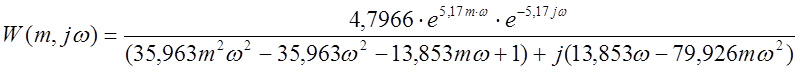 .
.
Для упрощения подставим в выражение (2.4)
значение колебательности ![]() :
:
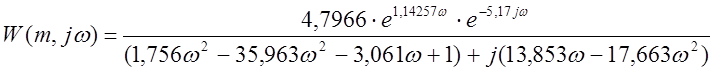 ;
;
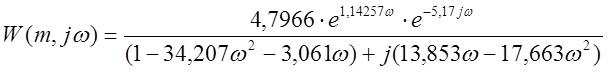 ;
;
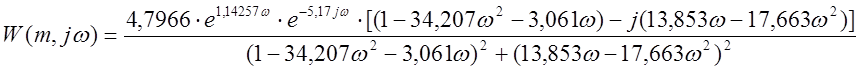 .
.
Представим
передаточную функцию ![]() в виде комплексного
числа:
в виде комплексного
числа:
![]() , (2.5)
, (2.5)
где
![]() и
и ![]() . (2.6)
. (2.6)
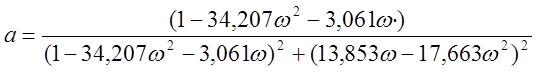 ;
;
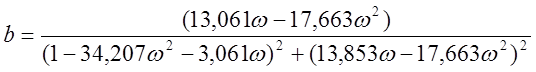 .
.
![]()
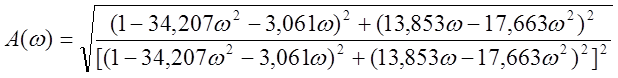 ;
;
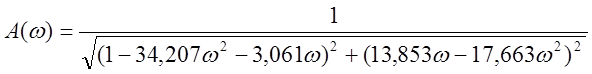 ;
;
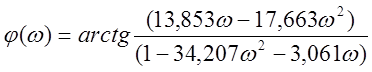 .
.
Окончательные
значения ![]() и
и ![]() для объекта:
для объекта:
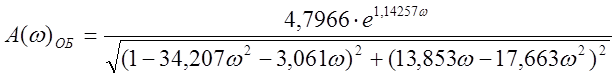 ;
;
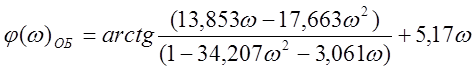 .
.
Исходя из условия (2.1), имеем:
![]() ,
, ![]() . (2.7)
. (2.7)
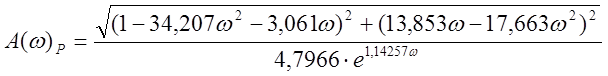 ;
;
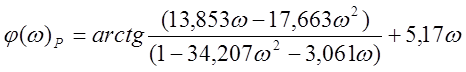 .
.
Рассчитаем параметры
ПИ-регулятора ![]() и
и ![]() вручную
для двух значений
вручную
для двух значений ![]() и
и ![]() ,
для остальных
,
для остальных ![]() точки
точки ![]() рассчитаем на ЭВМ. Для расчёта
параметров ПИ-регулятора
рассчитаем на ЭВМ. Для расчёта
параметров ПИ-регулятора ![]() и
и ![]() воспользуемся готовыми формулами:
воспользуемся готовыми формулами:
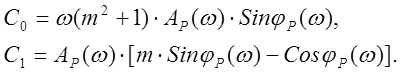 (2.8)
(2.8)
Для ![]() :
:
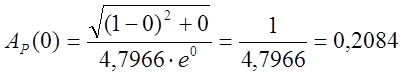 ;
;
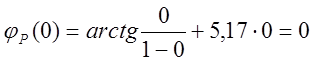 ,
,
тогда
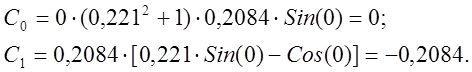
Для ![]() :
:
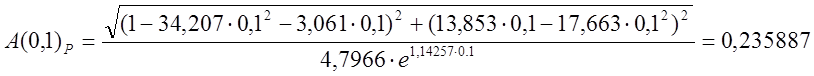 ;
;
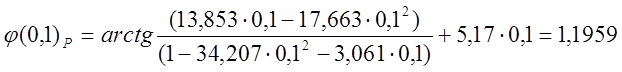 ,
,
тогда
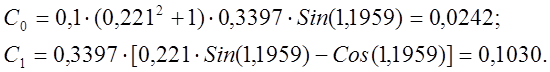
Программа для расчёта настроек ПИ-регулятора на языке Matlab:
function Max_Variant_13
n=0; w=0.001; m=0.221;
while n<=1000
p=(-m+1i)*(w*n);
n=n+1;
A=4.7966*exp(-p*5.17)/(35.963*p*p+13.853*p+1);
A0=1/A;
C0(n)=(w*n)*(m^2+1)*imag(A0);
C1(n)=m*imag(A0)-real(A0);
disp([n*w,C0(n),C1(n)]);
if C0(n)<0 n=1001;end
end
plot(C1,C0);
grid;
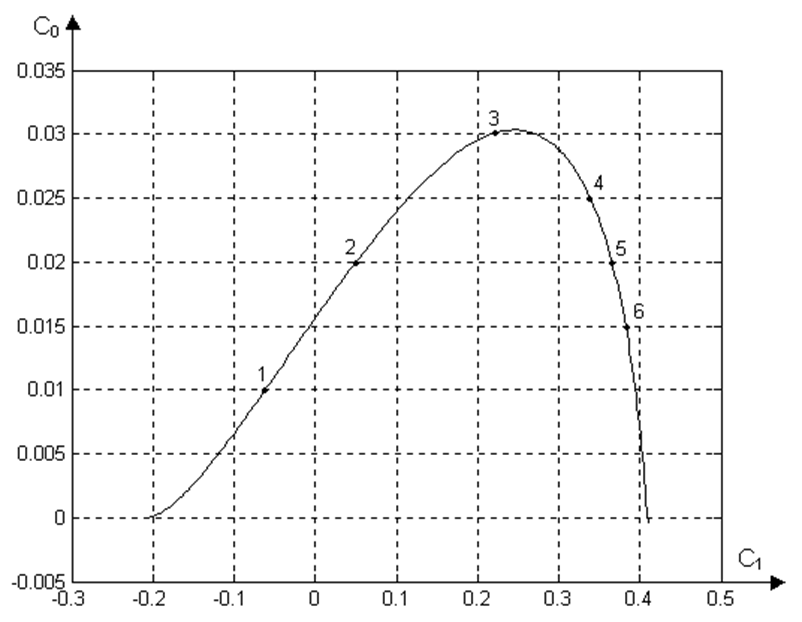
Возьмём несколько точек, лежащих на кривой равной степени затухания (рисунок 2.1) и посмотрим как будет изменятся процесс регулирования. Для этой цели будем использовать пакет MATLAB.
Таблица 2.1 – Выбранные точки на кривой равной степени затухания
|
Точка 1 |
Точка 2 |
Точка 3 |
Точка 4 |
Точка 5 |
Точка 6 |
|
w1 = 0,0560 |
w2 = 0,0860 |
w3 = 0,1320 |
w4 = 0,1710 |
w5 = 0,1830 |
w6 = 0,1920 |
|
С0 = 0,0102 |
С0 = 0,020 |
С0 = 0,03 |
С0 = 0,0252 |
С0 = 0,0201 |
С0 = 0,0150 |
|
С1 = -0,0591 |
С1 = 0,0502 |
С1 = 0,2197 |
С1 = 0,3374 |
С1 = 0,3649 |
С1 = 0,3823 |
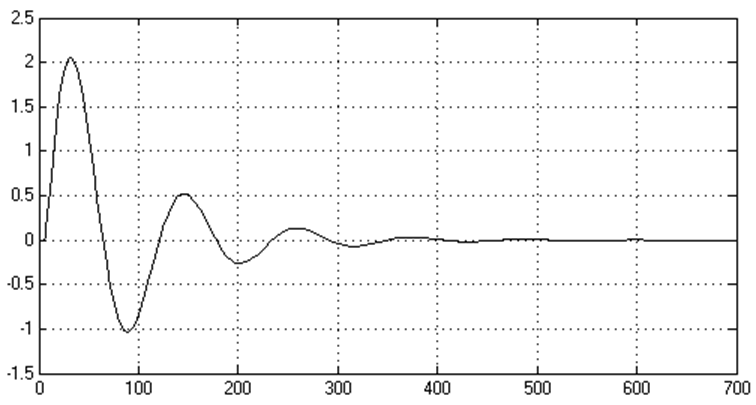
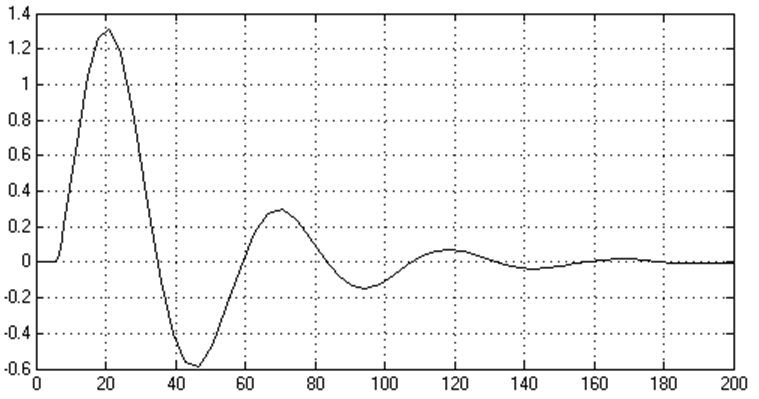
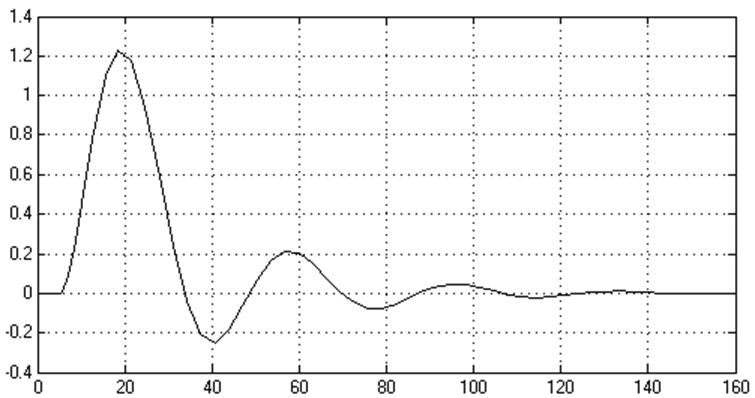
Ниже представлены графики процессов регулирования системы автоматического управления для каждой выбранной точки.
σ
 t
t
Рисунок 2.2 - График процесса регулирования САР (точка 1)
σ
 t
t
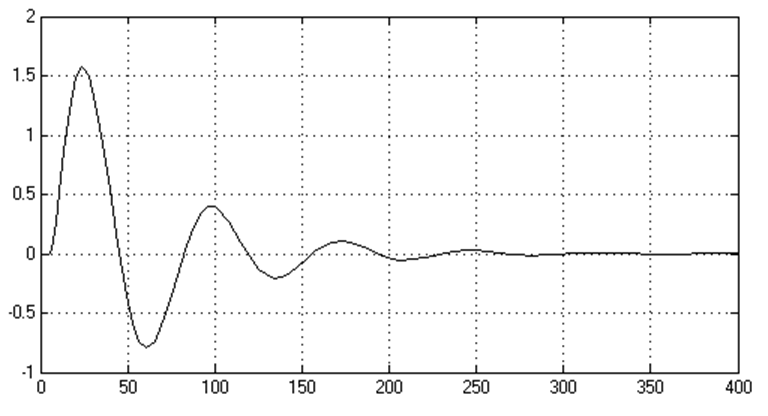
Рисунок 2.3 - График процесса регулирования САР (точка 2)
σ
 t
t
Рисунок 2.4 - График процесса регулирования САР (точка 3)
σ
 t
t
Рисунок 2.5 - График процесса регулирования САР (точка 4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.