Технологический процесс как объект управления, страница 2

      Статический режим реализуется клапаном.  Расход жидкости зависит от уровня Н и достаточно точно описывается выражением:

                         Q_ст = k_ис  Ö`H ,

где k_ис -  коэффициент, зависящий от размеров и формы отверстия истечения.

          С помощью уравнения материального баланса получаем статическую характеристику   ОУ    (уравнение  нелинейное):                                                                                         

                           Н = ( 1 / k_ис )²    Q²_пр  = ( 1 / k_ис )²    Q²_ст .

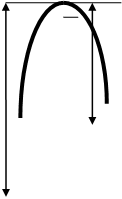
                                          Н

                                        Н_max        + DH                 С      С`

                                        Н₀                                           А

                                        Н_min         -D H           D     D`     

                                                                           a  

                                                                                   Q₀                        Q_пр

                           Рис.  Статическая характеристика ОУ.

       Для упрощения проектирования АСУ  используют линеаризацию характеристики

( переход от кривой CAD  к прямой  C`AD` в диапазоне значений Н₀  ± DH ) :

                            H  =  k  Q_пр = k  Q_ст,

где  k - коэффициент усиления для линеаризованного объекта (тангенс угла наклона

 k = tga ).

         Примером астатического  ОУ   может служить бак, из которого жидкость откачивается насосом с определенной скоростью.  Равновесие может наступить при любом уровне.  Такие   ОУ рассматриваются в динамическом режиме.

       При действии на вход объекта управления (ОУ)  возмущения  Х    на его выходе появляется отклонение величины У.   Протекает переходный процесс, который может быть колебательным  и неколебательным (апериодическим).  С течением времени амплитуда колебательного процесса может уменьшаться (затухающий переходный процесс), оставаться постоянной или увеличиваться (расходящийся процесс). Последние  два процесса неустойчивы.

       Переходный процесс характеризуется следующими  показателями:

  -  у₁  -  максимальным динамическим отклонением регулируемой величины У,

  -   у_ост -  остаточным отклонением регулируемой величины после окончания переходного процесса,

    - t _p -   время процесса регулирования, по окончании которого отклонение регулируемой величины от установившегося значения будет меньше заданного отклонения D у .

   у                                                     у

           у₁               y₁`          (а)                                      у<sub>1</sub>            y<sub>1</sub>`            (б)

 

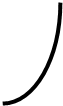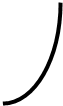                                                  2D у                                                                            2D у

                 у_ост у_ост

                  t _p                                       t                            t _p                                    t

 

       Рис.    Показатели качества переходного процесса: (а) - апериодического,  (б) - затухающего колебательного.

        Для построения математической модели  используется аналитический и экспериментально-аналитический методы.

        Аналитический метод описания  динамического режима предусматривает синтез зависимости нарушения статического равновесия

                        S  DH(t)  =   (  DQ_пр  (t)  -  DQ_ст  (t)  )  Dt,

где  S - площадь поперечного сечения бака.

        Сток  жидкости  из  бака  при  небольших  приращениях   можно описать линеаризированным уравнением:

                         DQ_ст  (t)  = 1/ k  DH(t).

При переходе к пределу при Dt ® 0 уравнение приобретает вид:

                        S  dDH(t) / dt  +   DH(t) / k  = D Q_пр  (t).

При умножении уравнения на 1/k  и введении обозначений: S k = T  - постоянная времени ОУ,   DH = y  -   регулируемая (выходная) величина,    DQ_пр = х  -  регулирующее воздействие (входная величина),  дифференциальное уравнение примет вид:

                        T  dy(t) / dt + y(t)  =  k  x(t).

       Экспериментальное-аналитическое определение характеристик  ОУ производят путем воздействия на находящийся в равновесии ОУ  возмущения (изменения входной величины).  Реакция  ОУ на воздействие называется кривой разгона.    С момента возмущения регулируемая величина регистрируется во времени до стабилизации ее на новом уровне для статического  ОУ  или до установления постоянной скорости для астатического  ОУ.

 Х

                                                x                  t

              T

    Y

 

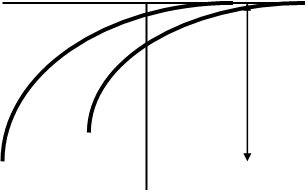
                       1             2                 y_ост  = k x

 

                                                                     t

                  t_е        T₂

       Рис.  Кривые разгона статических  ОУ.

       С помощью кривой разгона определяются k  и Т.   Коэффициент усиления k по каналу регулирующего воздействия определяется из соотношения:

                        k_x = y _ост / x,

где y_ост  - остаточное отклонение регулируемой величины от первоначального значения, х - величина скачкообразного изменения регулирующего воздействия.  Чем больше коэффициент усиления  k, тем чувствительнее объект к внешним воздействиям. Скорость изменения регулируемой величины в переходном процессе оценивается постоянной времени  Т.   Чем больше Т (чем инерционнее  ОУ ), тем труднее его регулировать. Для уменьшения  времени  Т  необходимо уменьшать емкость (размеры бака)  или  увеличивать нагрузку ОУ  (величину стока).

         Для  статических ОУ  кривая разгона

1 -  первого порядка, или одноемкостного, динамика которого описывается дифференциальным уравнением 1-ого порядка,