Проект автоматизации энергетического тракта содорегенерационного котла, страница 6

7 Расчетная часть

7.1 Расчет параметров настройки одноконтурных АСР методом незатухающих колебаний

В соответствии с этим методом, расчёт настроек ПИД-регулятора проводится в два этапа:

1) Расчёт критической настройки пропорциональной составляющей , (C₀ = С₂ = 0), при которой АСР будет находится на границе устойчивости, и соответствующее ей :  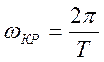;                                              2) Определение по  и  оптимальных настроек (,,) регулятора, обеспечивающих степень затухания .

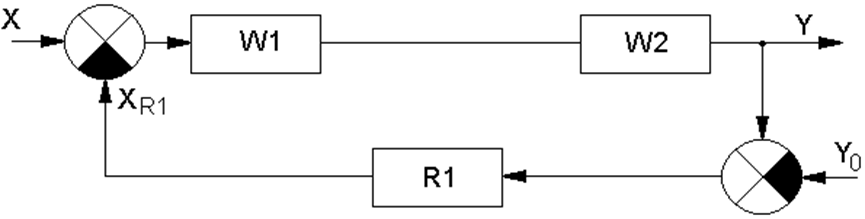
Рисунок 7.1 – Структурная схема одноконтурной АСР

Передаточные функции W₁ и W₂ будут иметь вид

;                  

;

;  

.

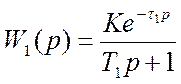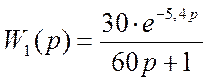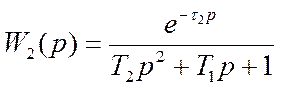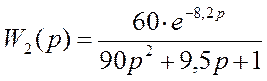Так как интегрирующая и дифференциальная составляющие из условия расчёта равны нулю (C₀ = С₂ = 0), следовательно, при помощи пакета MATLAB (рисунок 7.2) подбираем пропорциональную составляющую .

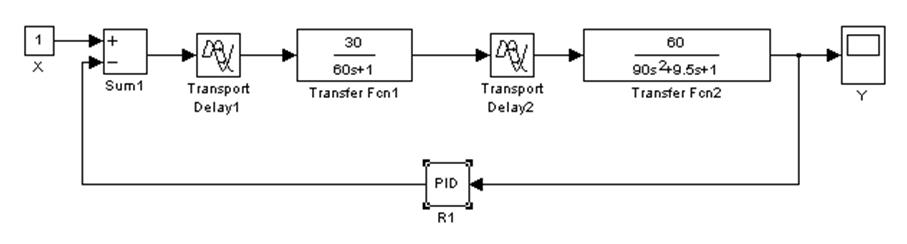
Рисунок 7.2 – Модель одноконтурной АСР в пакете Simulink

Из рисунка 7.3 видно, что период автоколебаний, при котором АСР находится на границе устойчивости, равен: T = 87 сек.

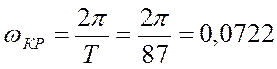 рад/с.

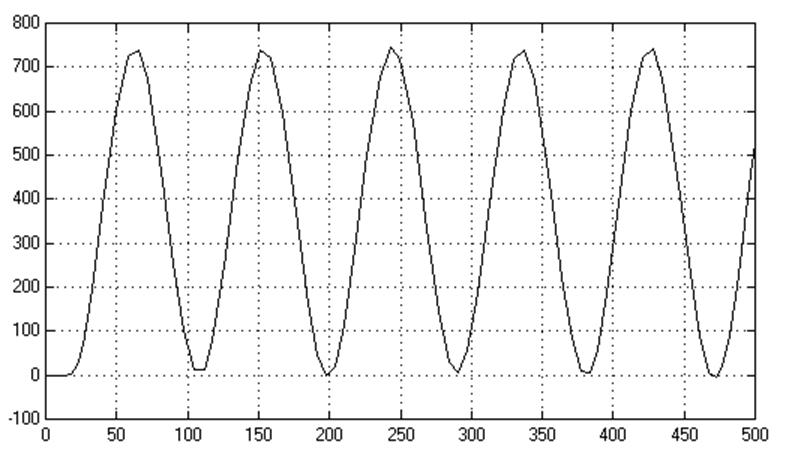
Рисунок 7.3 – Автоколебательный процесс.

Оптимальные настройки ПИД-регулятора находим по формулам:

,   ,   

;           

;

.

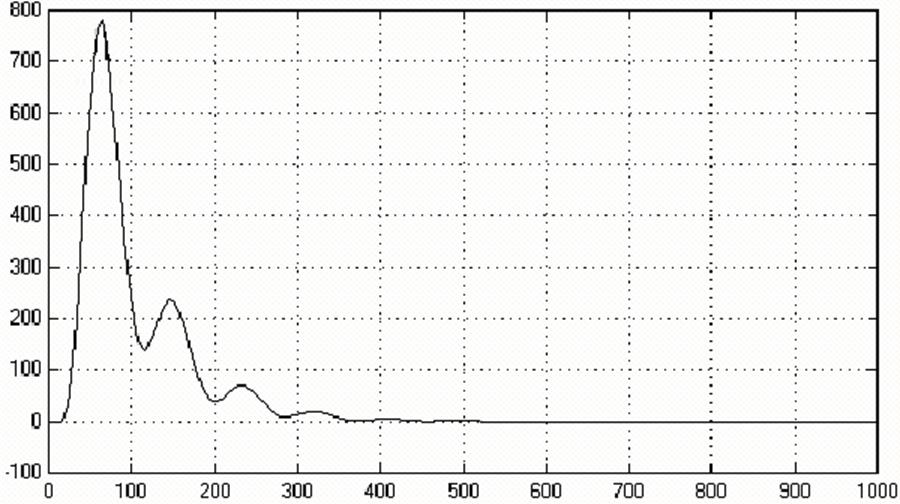
Рисунок 7.4 – Процесс регулирования с оптимальными настройками ПИД-регулятора.

7.2 Расчет настроек регуляторов каскадной АСР

Расчет каскадной АСР предполагает определение настроек основного и вспомогательного регуляторов при заданных динамических характеристиках объекта по основному и вспомогательному каналам.

Поскольку настройки основного и вспомогательного регуляторов взаимозависимы, расчет их проводят методом итераций.

На каждом шаге итерации рассчитывают приведенную одноконтурную АСР, в которой один из регуляторов условно относится к эквивалентному объекту.

В качестве основного регулятора будем использовать ПИ-регулятор, в качестве вспомогательного – П-регулятор.

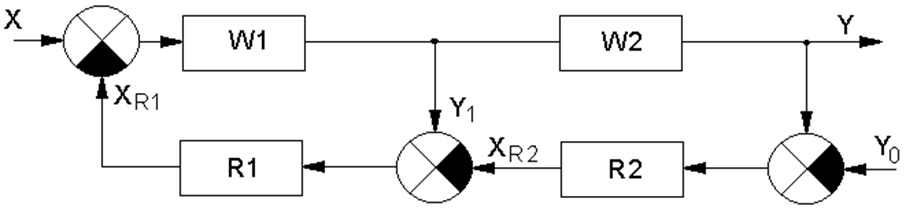
Рисунок 7.5 – Структурная схема каскадной АСР

Передаточные функции W₁ и W₂ будут иметь вид

;              

;

;

.

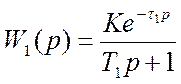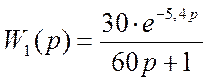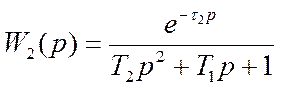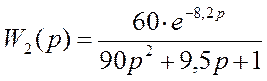Передаточные функции регуляторов имеют вид:

,

.

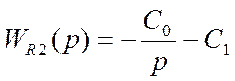Передаточная функция эквивалентного объекта для основного регулятора представляет последовательное соединение замкнутого вспомогательного контура и основного канала регулирования и определяется по формуле: .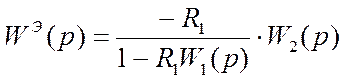                      

Передаточная функция эквивалентного объекта для вспомогательного регулятора является параллельным соединением вспомогательного канала и основной разомкнутой системы и определяется по формуле: .                        

Расчет начинаем с основного регулятора. Этот метод используется в тех случаях, когда инерционность вспомогательного канала намного меньше чем основного.

На первом шаге принимаем следующее допущение о том, что рабочая частота основного регулятора намного меньше, чем вспомогательного . Тогда при  .

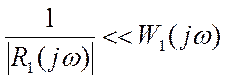Приняв это допущение выражение можно записать

                             .

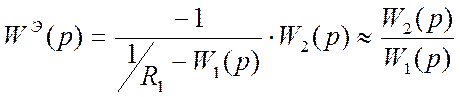Таким образом в первом приближении настройки основного регулятора не зависят от вспомогательного регулятора и находятся по формуле:

,                                

                                                                        

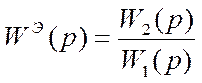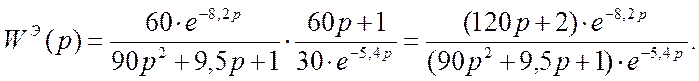
Далее используя полученную передаточную функцию,  определяем настройки основного регулятора, для чего строим линию равной степени затухания и выбираем на ней оптимальную точку (рисунок 7.6).

Для построения линии равной степени затухания используем MatLab. Программа для расчёта настроек ПИ-регулятора на ЭВМ имеет следующий вид:

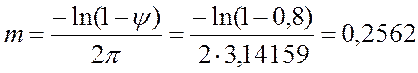
function F

i=0; w=0.001; m=0.2562;

  while i<=1000

    p=(-m+1i)*w*i;

    i=i+1;

    A=((100*p+2)*exp(-p*8.07))/((75*p*p+8.66*p+1)*exp(-p*5.38));   

    A0=1/A;

    C0(i)=w*i*(m^2+1)*imag(A0);

    C1(i)=m*imag(A0)-real(A0);

        if C0(i)<0

            i=1005;

        end

   end

plot(C1,C0),

grid,

title('График');

xlabe('C1');

ylabe('C0');

end

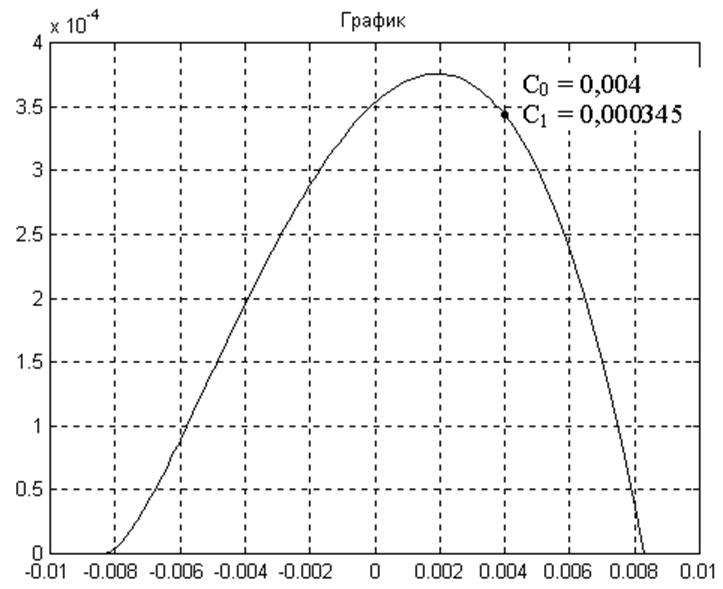
Рисунок 7.6 – Линия равной степени затухания для основного регулятора

На втором шаге рассчитываем настройки вспомогательного регулятора для эквивалентного объекта с передаточной функцией, в которую подставляем полученные настройки С₁ = 0,000345 и С₀ = 0,004 основного регулятора:

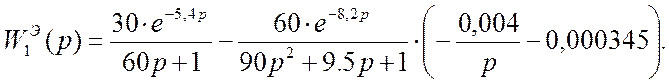
Далее используя полученную передаточную функцию определяем настройки вспомогательного П-регулятора, для чего строим линию равной степени затухания и выбираем на ней оптимальную точку, в которой С₁ = 0,1  (рисунок 7.7).

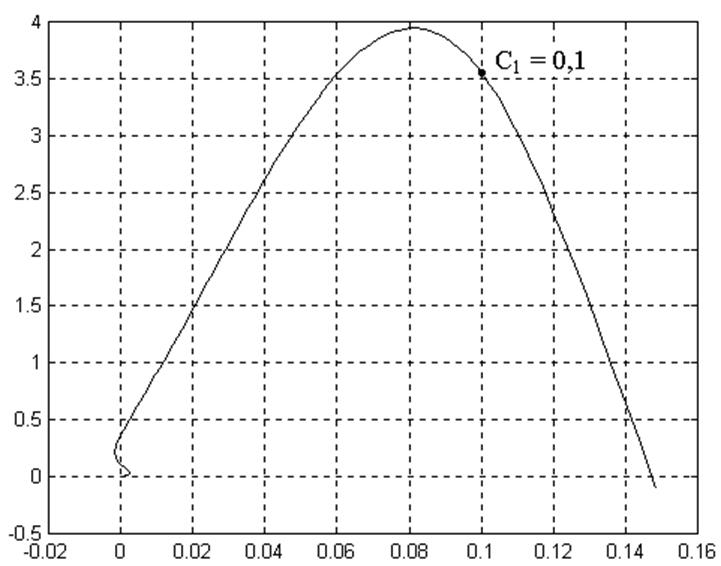
Рисунок 7.7 – Линия равной степени затухания для вспомогательного регулятора

Получив значения оптимальных настроек регуляторов, моделируем каскадную АСР в пакете Simulink (рисунок 7.8).

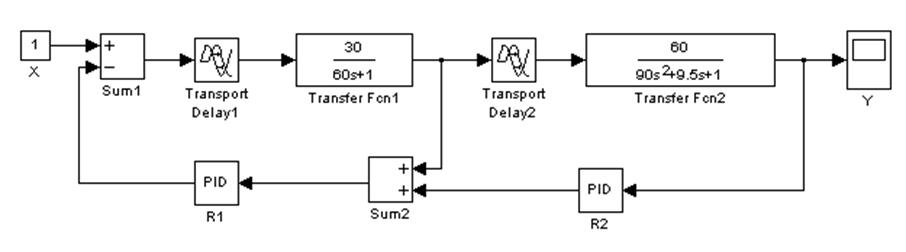
Рисунок 7.8 – Модель каскадной АСР в пакете Simulink

После настройки регуляторов получаем оптимальный процесс регулирования (рисунок 7.9).

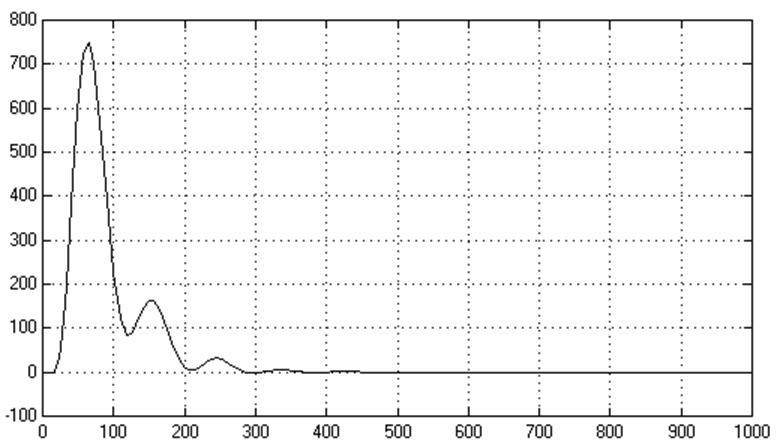
Рисунок 7.9 – Процесс регулирования при оптимальных настройках регуляторов каскадной АСР

Сравним полученный процесс регулирования с процессом при использовании эквивалентной одноконтурной АСР и оптимально настроенного ПИ-регулятора.

Таблица 7.10 – Сравнение одноконтурной и каскадной АСР

Можно сделать вывод, что использование каскадной системы регулирования предпочтительнее, так как качество процесса регулирования заметно улучшается.