Х→ μ ![]() .
.
Задачи моделирования CAP уровня жидкости в емкости
1. Выбрать значения переменных в передаточных функциях, входящих в модель.
2. Проанализировать переходной процесс при различных настройках регулятора.
3. Исследовать процесс регулирования уровня жидкости в баке при изменении давления на выходе крана оттока.
4. Оптимизировать настройки регулятора.
Модель системы регулирования высоты жидкости в резервуаре
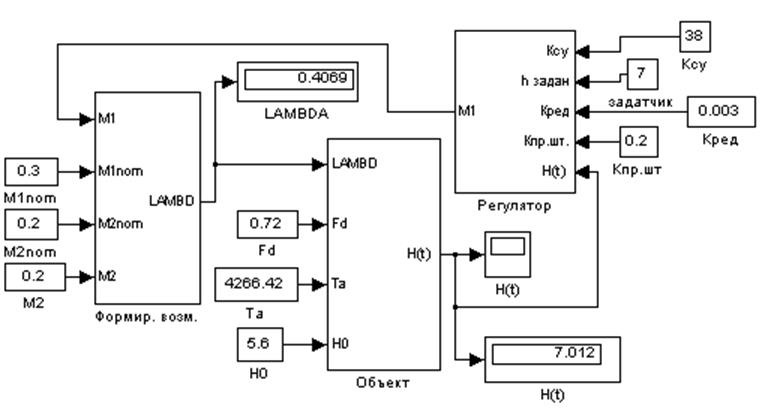
Модель системы регулирования высоты жидкости в резервуаре
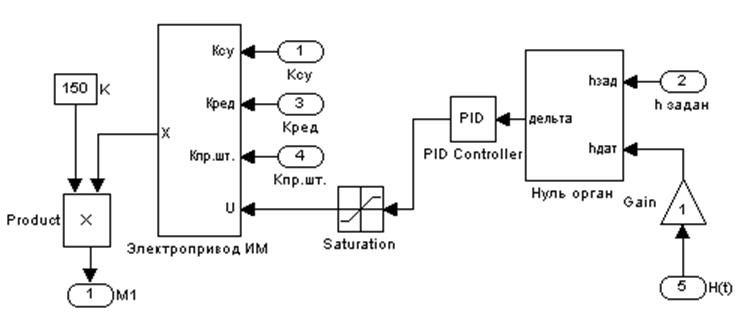
Модель системы регулирования
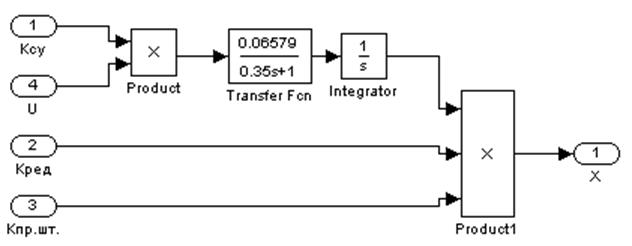
Блок электропривода ИМ
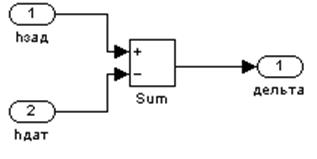
Блок «Нуль – орган»
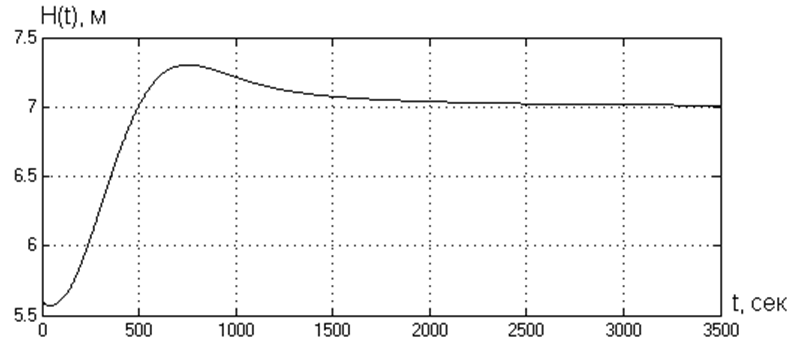
Процесс регулирования
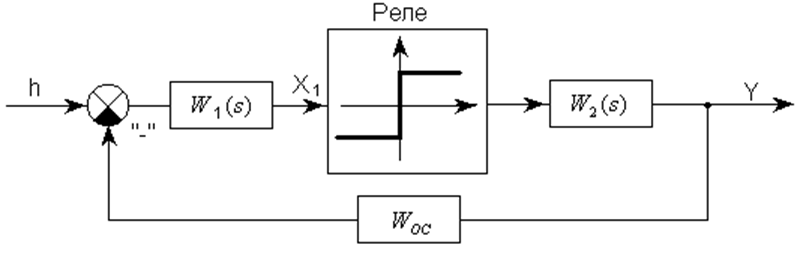
Задание на выполнение самостоятельной работы
Определить частоту и амплитуду автоколебаний САР, структурная схема которого представлена на рисунке, и предложить данную схему в «железе».
![]() первого линейного звена равна
первого линейного звена равна 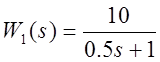 .
.
![]() второго линейного звена равна
второго линейного звена равна 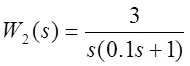 .
.
Функция В нелинейного звена равна В = 10.
![]() .
.
Аналитическая модель системы
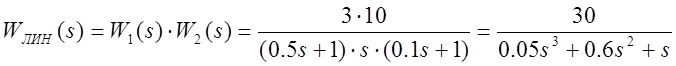 .
.
Коэффициенты гармонической линеаризации для нелинейного звена (идеальное реле) представленного на схеме:
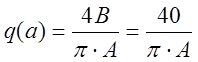 ;
; ![]() .
.
При гармонической линеаризации нелинейного звена, его передаточная функция будет иметь вид:
![]() ;
; 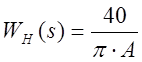 .
.
Передаточная функция разомкнутой системы:
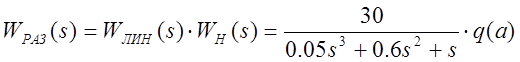 .
.
Передаточная функция замкнутой системы:
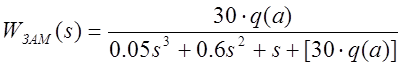 .
.
Характеристическое уравнение свободных колебаний системы (знаменатель передаточной функции замкнутой системы):
![]() .
.
Для нашей системы:
![]() , отсюда:
, отсюда: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Аналитическое исследование системы
Определим параметры автоколебаний, для чего используем критерий Гурвица. Составим определитель матрицы Гурвица 3-го порядка:
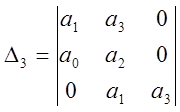 .
.
Подставим значения:
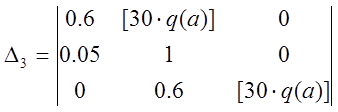 .
.
Из критического
условия ![]() соответствующего наличию
автоколебания. Найдём их амплитуду:
соответствующего наличию
автоколебания. Найдём их амплитуду:
![]() ;
;
![]() или
или ![]() .
.
Отсюда: ![]() или
или
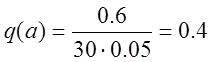 .
.
Зная величину ![]() , определяем значение амплитуды
колебания А:
, определяем значение амплитуды
колебания А:
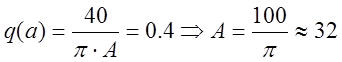 .
.
Рассмотрим способ определения частоты автоколебаний возникающих в системе. Характеристическое уравнение системы имеет вид:
![]() .
.
Подставим в него
значение ![]() . Тогда уравнение примет следующий
вид:
. Тогда уравнение примет следующий
вид:
![]() .
.
Разделим полученное уравнение на мнимую и действительную части:
![]() ;
;
![]() .
.
Определим ![]() из любого уравнения:
из любого уравнения:
![]() ;
; ![]() .
.
Отсюда: ![]()
![]()
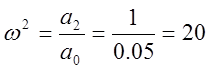
или 
![]()
![]()
![]()
![]() .
.
Схема в «железе»
Среди нелинейных систем регулирования особое место занимают релейные системы, в которых сигнал рассогласования подаётся на усилительно-исполнительные устройства через релейно-контактные элементы.
Широкое распространение релейных систем регулирования объясняется их высоким быстродействием, простотой дешевизной и малыми габаритными размерами.
Введение релейно-контактного элемента приводит к возникновению колебаний определённой частоты и амплитуды (автоколебаний). Амплитуда автоколебаний в релейной системе должна быть ограничена требованиями точности. Для ограничения амплитуды автоколебаний обычно используют корректирующие устройства.
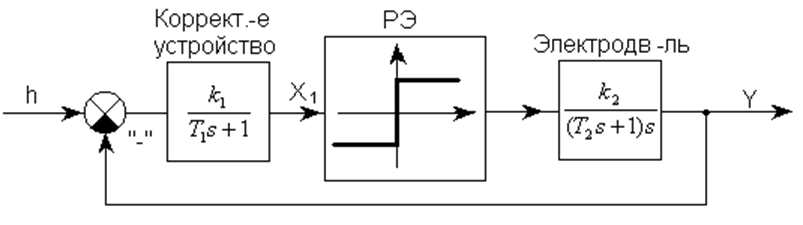
Схема имеет последовательное корректирующее устройство, включённое после сравнивающего устройства до релейного элемента РЭ.
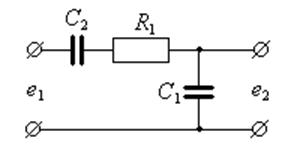 Корректирующее устройство
Корректирующее устройствоЛинейное корректирующее устройство:
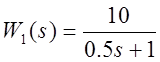 , где
, где 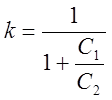 ;
;
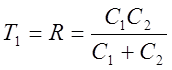 .
.
Релейные усилители (реле) являются одновременно усилителями и управляющими элементами для электродвигателей. Поэтому они всегда применяются в комплексе с соответствующими электродвигателями. Электрическое реле в общем случае представляет собой промежуточный элемент, производящий в действие одну или несколько управляемых цепей.
 Сигналы, получаемые
от чувствительных элементов или датчиков, в большинстве случаев недостаточны по
мощности, чтобы непосредственно привести в движение регулирующий орган. Это
обусловливает применение усилителей. В ряде случаев усилители наряду с функцией
усиления мощности выполняют функцию преобразования выходного сигнала
чувствительного элемента в другой вид, более удобный для работы системы
автоматического регулирования.
Сигналы, получаемые
от чувствительных элементов или датчиков, в большинстве случаев недостаточны по
мощности, чтобы непосредственно привести в движение регулирующий орган. Это
обусловливает применение усилителей. В ряде случаев усилители наряду с функцией
усиления мощности выполняют функцию преобразования выходного сигнала
чувствительного элемента в другой вид, более удобный для работы системы
автоматического регулирования.
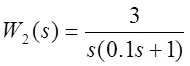 .
.
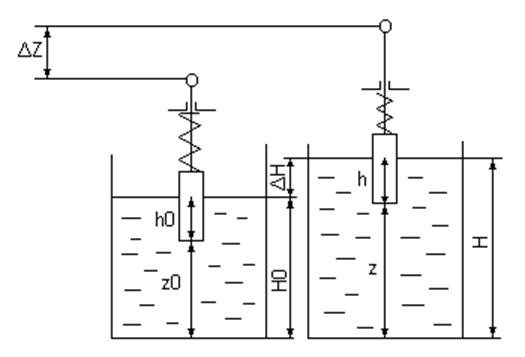
Напишем уравнение баланса:
![]() ;
; ![]() - поддерживающая
сила;
- поддерживающая
сила;
![]() - востанавливающая сила.
- востанавливающая сила.
Для востанавливающей :
![]()
![]() - вес поплавка;
- вес поплавка;
![]() - начальное усилие
пружины (настройка чувствительного элемента);
- начальное усилие
пружины (настройка чувствительного элемента);
![]() - жесткость
пружины;
- жесткость
пружины;
![]() - деформация
пружины.
- деформация
пружины.
Для поддерживающей силы:
![]()
![]() - удельный вес
жидкости;
- удельный вес
жидкости;
![]() - площадь
поперечного сечения поплавка;
- площадь
поперечного сечения поплавка;
![]() - высота погружения
поплавка.
- высота погружения
поплавка.
![]()
Отметим перемещение поплавка будет меньше
изменению уровня ![]()
![]()
![]()
![]()
Имеющиеся в обеих частях уравнениячлены
являются функциями определяющими фактор устойчивости ![]() :
:
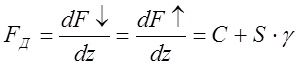
если ![]() всегда >0 то система
устойчива
всегда >0 то система
устойчива
Фактор устойчивости будет >0 поскольку все велечины входящие в уравнение физически не могут быть отрицательными
Из уравнения баланса z равно
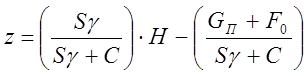
Составим уравнение динамики:
Правая часть:![]()
Левая часть: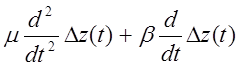
![]() - коэффициент пропорциональности
- коэффициент пропорциональности
![]() - приведенная масса
- приведенная масса
Разберёмся с правой частью:
Правую составляющую разложим в ряд Тейлора
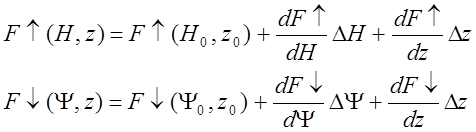
Последующей подстановкой соответствующих преобразований получим:
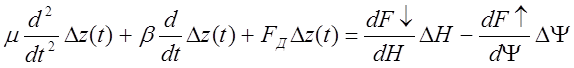
Введём относительные переменные
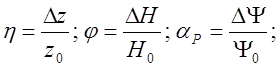
и разделим все коэффициентына коэффициентпри входной переменной
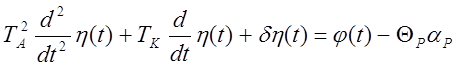
где 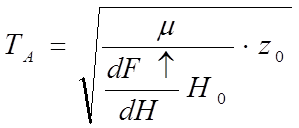 - время чувствительного элемента
- время чувствительного элемента
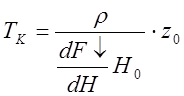 - время катаракта
- время катаракта
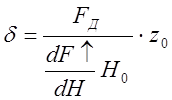 - степень не
равномерности
- степень не
равномерности
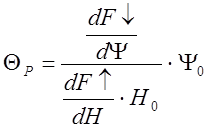 - фактор настройки
чувствительного элемента
- фактор настройки
чувствительного элемента
Для большенства случаев вторым порядком можно пренебреч.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.