Общие методы программирования решения дифференциальных уравнений, страница 2

Полученная модель действительна для объектов «А» и «Б».

Модель В

Примем производительность насоса постоянной. Тогда дифференциальное уравнение, представляющее математическую модель данного объекта, будет иметь вид:

,

где F_бака – площадь поперечного сечения бака, м³;

      H(t) – высота столба жидкости в бака, м;

      Q_пр – расход жидкости на притоке, м/с;

      Q_от – расход жидкости на оттоке, м/с.

Отметим, что в правой части полученного уравнения нет слагаемых, зависящих от переменной левой части или от ее производной. Это значит что структурная схема модели не будет содержать обратных связей.

Разрешим уравнение относительно старшей производной:

.

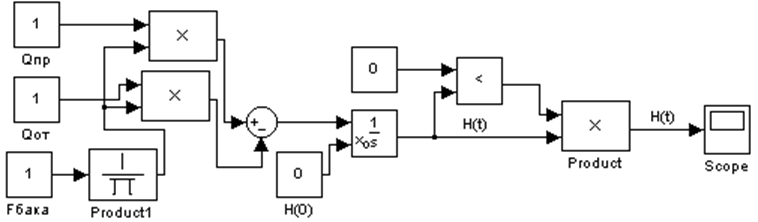Полученное уравнение в Matlab можно изобразить в виде:

Рисунок 6 – Модель одноемкостного объекта

Модель двухемкостного объекта с запаздываем

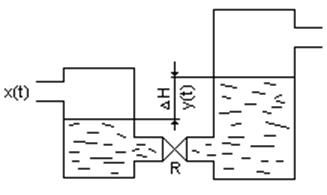
Рисунок 1 – Статическое изображение двухемкостного объекта

x(t) – величина возмущающего воздействия; y(t) – величина регулируемого параметра; R – местное сопротивление.

Примерами двухемкостных объектов с запаздыванием могут служить теплообменник поверхностного типа, варочных котел непрямого подогрева или ректификационная колонна. Характерным для них является наличие незначительного местного сопротивления между емкостями. Последнее означает, что все они могут удовлетворительно аппроксимироваться апериодическим звеном второго порядка с запаздыванием которое может быть описано уравнением второй степени с постоянными коэффициентами:

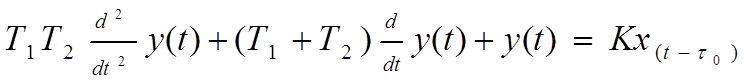          (1)

где x(t) – величина возмущающего воздействия;

      y(t) – изменение регулируемого параметра.

В операторной форме уравнение (1) будет и меть вид:

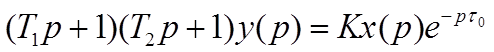.                       (2)

Передаточная функция:

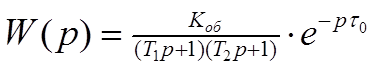,                              (3)

где Т₁, Т₂ – постоянные времени отдельных емкостей;

       К_об – коэффициент передачи объекта.

Для аналитического построения кривой разгона объекта можно воспользоваться решением дифференциального уравнения (1), которое имеет вид:

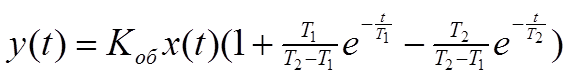.                      (4)

В качестве модели объекта можно использовать как само дифференциальное уравнение (1), так и его решение в форме (4).

Создадим в Matlab модель решения уравнения (1). Общий ее вид:

 

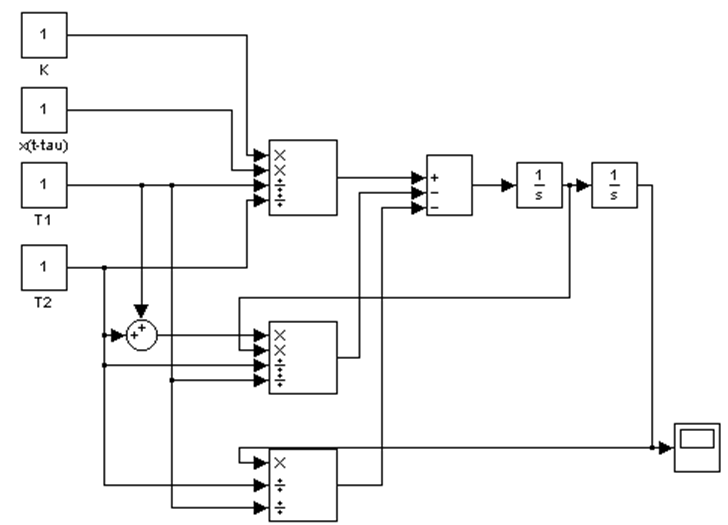
Рисунок 2 – Модель решения уравнения (1)

Создадим в Matlab модель решения уравнения (4). Общий ее вид:

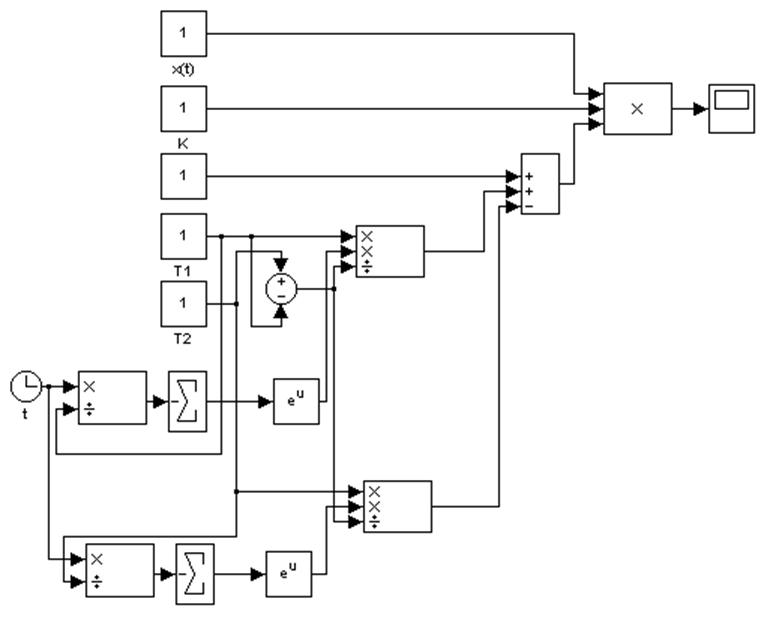
Рисунок 2 – Модель решения уравнения (4)

Начальное транспортное запаздывание двухемкостных объектов обычно принимают (0,4…0,5)Т₁.

Переходное транспортное запаздывание обусловлено наличием сопротивления между отдельными емкостями объекта.

Содержательное описание объекта

Имеем емкость-накопитель кислоты, задача которой, в случае отказа подачи рабочего тела в линию, в течение определенного времени поддерживать поступле­ние кислоты на вход последующего технологического аппарата.

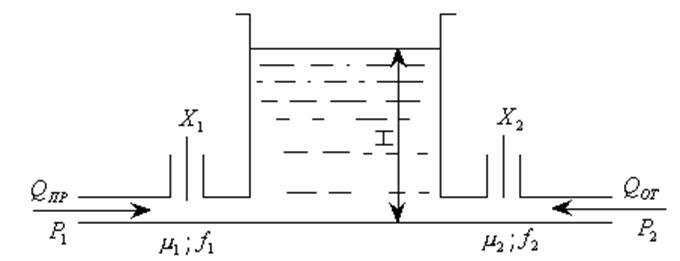
Объект регулирования - резервуар с линиями подвода и отвода жидкости.

Рабочее тело - кислота. 

Удельный вес γ = 10240, [Н/м³].

Регулируемый параметр - высота жидкости в резервуаре Н_о.

Конструктивные параметры объекта

Наименование	Обозначение	Значение
Диаметр резервуара	D	6 м
Высота резервуара		10 м
Диаметр подводящей трубы	d1	0,1 м
Диаметр отводящей трубы	d2	0,15 м

Краны, расположенные на входе и выходе резервуара, имеют линейную рас­ходную характеристику.

Номинальные значения параметров процесса:

Наименование	Обозначение	Значение
Давление на входе	p1н	21,58 × 104, Па
Давление на выходе	P2н	2,943 × 104, Па
Коэффициент истечения для крана на входе	μ1ном	0,3
Коэффициент истечения для крана на выходе	μ2ном	0,2

 Составление аналитической модели объекта

Для составления аналитической модели, мы должны решить две задачи:

· опре­делить время разгона объекта;

· опре­делить коэффициенты самовыравнивания на линиях при­тока и оттока жидкости объекта.

Определяем время разгона объекта.

Решение задачи начнем с того, что определим высоту столба жидкости над дном резервуара Н₀

Уравнение баланса:

,

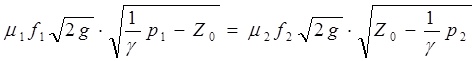где Z₀ – противодавление (уровень жидкости в системе).

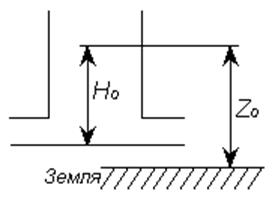Находим численные значения коэффициентов для

 данного уравнения в установившемся режиме:

;

;

;

.

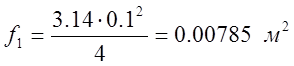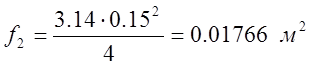
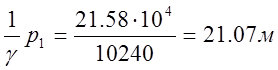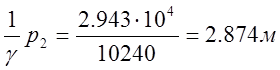С учетом вычисленных значений коэффициентов балансовое уравнение при­нимает следующий вид:

,

.

Разрешив последнее уравнение относительно Zo, получаем:

Z₀ = 8,474 м.

При этом расход жидкости Q₀ :

q₀= 0,0371, [м³/c].

Высота столба жидкости над дном резервуара Н₀ равна разности между вычисленным значением Z₀ и высотой столба жидкости Z_Р2Н, эквивалентной давлению подпора р_2н.

,

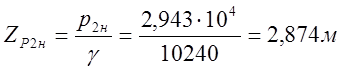откуда

м.

Площадь поперечного сечения резервуара равна:

.

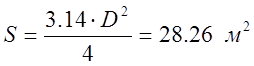Тогда аккумулированный в объем жидкости равен:

V =S × Но = 28,26 × 5,6 = 158,284 м³.

Время разгона:

.

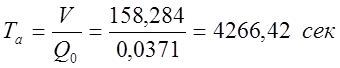Определяем коэффициенты самовыравнивания на линии притока и оттока жидкости объекта.

Перепишем уравнения притока и оттока жидкости, выразив значение уровня жидкостив гидравлической системе в установившемся режиме Zo через высоту столба жидкости над дном резервуара Но (Zo = Но +2.847):