![]() (34)
(34)
Выражение для ЛАЧХ имеет вид:
![]() (35)
(35)
![]() (36)
(36)
По оси абсцисс откладываем логарифмы частот сопряжений и через них проводим вертикальные асимптоты. Находим границу низкочастотной области. Откладываем по оси ординат полученное значение и проводим параллельную линию оси абсцисс до пересечения с первой асимптотой. Строим ЛАЧХ, основываясь на том, что числитель дает наклон (+20дБ/дек), знаменатель дает наклон (- 20дБ/дек).
Cтроим ЛАЧХ разомкнутой системы. От точки 20lg308,66 до сопрягающей частоты w2 строим прямую с наклоном 0 дБ/дек. Далее до сопрягающей частоты w1 – с наклоном -20 дБ/дек. После w1 – наклон 40 дБ/дек.
 В
приложении 1 представлена ЛАЧХ данной системы.
В
приложении 1 представлена ЛАЧХ данной системы.
4.2 Построение желаемой ЛАЧХ
Желаемой называют асимптотическую ЛАЧХ разомкнутой системы, имеющую, желаемые статические и динамические свойства.
Построение желаемой ЛАЧХ основывается на оценках качества: величина перерегулирования (30%); время перерегулирования (3 с).
Найдем частоту среза по формуле:
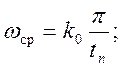 (37)
(37)
где к0 - коэффициент, определяемый из номограммы Солодовникова. Тогда подставив числовые значения, получим:
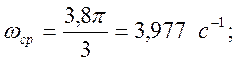 (38)
(38)
![]() ;
(39)
;
(39)
Теперь определим сопрягающую частоту, которая ограничивает средне-частотную область слева и справа, найдя коэффициенты для этих частот по соответствующей номограмме. Проводим прямые с ординатой 14 дБ и -14 дБ и обрезаем среднюю асимптоту.
Совмещаем высокочастотную ассимптоты желаемой ЛАЧХ и действительной ЛАЧХ. Наклоны желаемой характеристики в области высоких частот совпадают с наклонами неизменяемой части системы.
Построим ЛФЧХ по формуле:
![]() (40)
(40)
Задаваясь числовыми значениями частоты, составим таблицу значений ЛФЧХ (таблица 1). По полученным значениям строим график ЛФЧХ (приложение1).
 По
графику определим:
По
графику определим:
- запас устойчивости по модулю H M=10дБ;
- запас устойчивости по фазе φ˚=10˚.
Таблица 1 . Расчет ЛФЧХ
|
ω |
0 |
1 |
10 |
100 |
|
φ(ω) |
-90˚ |
-114,37˚ |
-184,19˚ |
-251,3˚ |
По полученным данным, следует, что система имеет не достаточный запас устойчивости.
Изложенный метод построения желаемой ЛАЧХ содержит некоторые допущения. Кроме того, графические этапы расчета вносят неизбежные неточности. Поэтому расчет чаще всего дает лишь приближенные значения параметров системы.
4.3 Построение ЛАЧХ и расчет передаточной функции корректирующего устройства
В следящих линейных системах целесообразней использовать последовательные корректирующие устройства (КУ). Построим ЛАЧХ корректирующего устройства, которая изображена в приложении 1. Пусть наше корректирующее устройство включено последовательно в электрическую часть цепи. Следовательно, находится по формуле:
![]() (41)
(41)
где ![]() и
и ![]() соответственно
желаемая ЛАЧХ и ЛАЧХ неизменяемой части.
соответственно
желаемая ЛАЧХ и ЛАЧХ неизменяемой части.
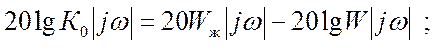 (42)
(42)
По ЛАЧХ корректирующего устройства находим передаточную функцию:

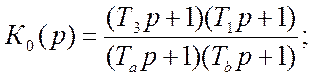 (43)
(43)
Из графика следует:
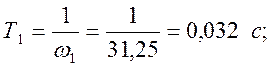 (44)
(44)
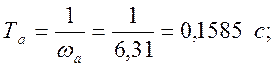 (45)
(45)
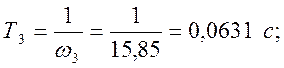 (46)
(46)
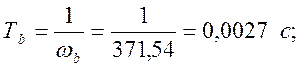 (47)
(47)
По виду передаточной функции определяем корректирующее звено:
![]() (48)
(48)
![]() (49)
(49)
![]() (50)
(50)
Рисунок 5 – Принципиальная схема корректирующего устройства
Произвольно зададим один из параметров корректирующего звена. Положим:
![]() (51)
(51)

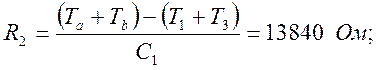 (52)
(52)
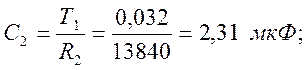 (53)
(53)
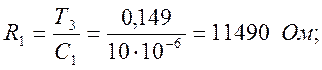 (54)
(54)
Передаточная функция привода с корректирующим звеном:
![]()
![]() (55)
(55)
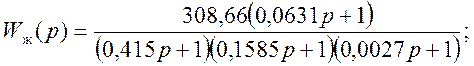 (56)
(56)
4.4 Анализ системы с корректирующим устройством
Для оценки качества системы построим переходный процесс системы с передаточной функцией (56), аналогично разделу 3.3:
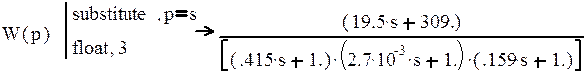 (57)
(57)
Теперь перейдем к h(t) с помощью обратного преобразования Лапласа:
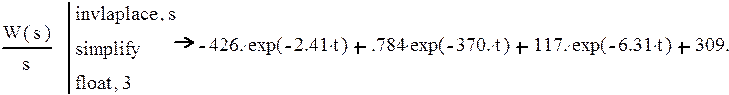 (58)
(58)
И получим уравнение переходного процесса:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.