Выбираем тахогенератор постоянного тока
ПТ – 31/1 [4, 434].
Технические данные:
- частота вращения, n………………..………………………………..200 об/мин; -- напряжение, U……………………………………………………………..230 В;
- ток якоря, Iя…………………………………………………………………0,1 А;
- ток возбуждения, Iв……………..………………………………………….1,1 А;
- сопротивление якорной цепи, Ra…………………………………………380 Ом;
- сопротивление обмотки возбуждения, Rя………………………………..41,6 Ом.
Передаточная функция тахогенератора имеет следующий вид:
(18)
где kтг – крутизна характеристики тахогенератора.
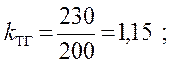(19)
3
СТРУКТУРНАЯ СХЕМА ЛОКАЛЬНОЙ СИСТЕМЫ И
ИССЛЕДОВАНИЕ ЕЕ НА УСТОЙЧИВОСТЬ
3.1 Структурная схема неизменяемой части системы
К неизменяемой части принято относить исполнительные органы, усилители мощности и измерительные средства. К неизменяемой части системы относят электронные усилители, преобразователи, микропроцессоры, различные дополнительные средства компенсации сигналов и устройства коррекции динамических характеристик.
Определив передаточные функции всех элементов системы, строим структурную схему (рисунок 3).
|
|
||||
|
|
 |
Рисунок 3 – Структурная схема системы
Передаточная функция замкнутой системы имеет вид:
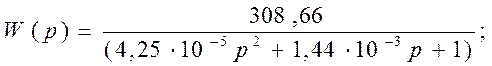(20)
В настоящей системе изменяемой частью является микропроцессор, так как его замена не вызовет изменения в передаточной функции системы.
3.2. Исследование системы на устойчивость
В исследуемой системе разомкнем обратную связь и определим устойчивость системы.
Передаточная функция разомкнутой системы имеет вид:
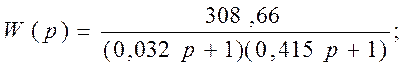(21)
Определим устойчивость системы. Для
этого воспользуемся алгебраическим критерием Гурвица.
Критерий
Гурвица формирует условие устойчивости в виде определителя.
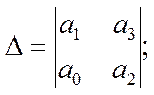(22)
где а0, а1, а2, а3 – коэффициенты характеристического уравнения.
Условие устойчивости по Гурвицу сводится к тому, чтобы при
все диагональные миноры главного определителя
были больше нуля.
За характеристическое уравнение примем выражение, стоящее в знаменателе передаточной функции разомкнутой системы:
; (23)
(24)
В этом уравнении а0=0,01328; а1=0,447; а2=1; а3= 0. Получаем:
(25)
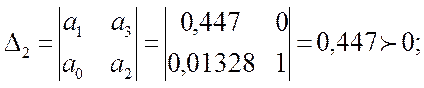(26)
Так как коэффициенты и определители уравнения больше нуля, то система в разомкнутом состоянии устойчива.
3.3 Построение переходного процесса и оценка качества системы
Для оценки качества системы построим переходный процесс для разомкнутой части с передаточной функцией (21).
Если на вход подается единичная ступенчатая функция 1(t), тогда выходной сигнал равен:
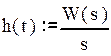; (27)
;
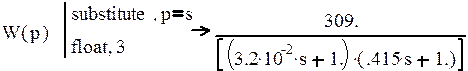(28)
Теперь перейдем к h(t) с помощью обратного преобразования Лапласа:
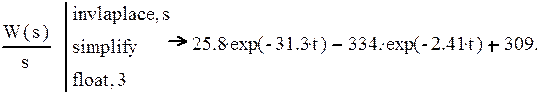; (29)
И получим уравнение переходного процесса:
; (30)
По данному уравнению (30) на рисунке 4 построим график.
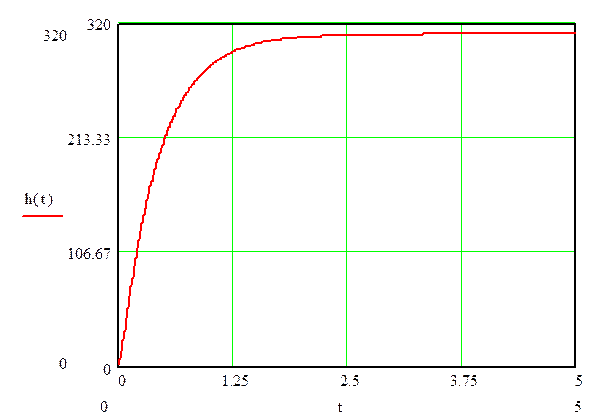
Рисунок 4 - График переходного процесса системы.
Исходя из полученной переходной функции h(t) проведем оценку качества системы:
- Установившееся значение переходного процесса hуст = 310;
- Максимальное значение переходного процесса hуст = 310 ;
- Время переходного процесса t n = 3с;
- Время перерегулирования переходного процесса d % =0.
4.
СИНТЕЗ СИСТЕМЫ МЕТОДОМ
ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
4.1 Построение ЛАЧХ неизменяемой части системы
Микропроцессор по принципу работы является машиной дискретного действия, которая выдает результаты через установленные периоды повторения. В промежутках между выдачей команд выход микропроцессора сохраняет свое значение.
Асимптотическая ЛАЧХ представляет собой ломаную линию, имеющую точки излома в сопрягаемых частотах, определяемых постоянными времени звеньев:
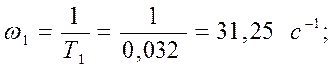(31)
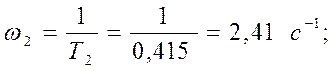(32)
Прологарифмируем полученные частоты:
(33)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
