Разработка управляющих программ для станков с ЧПУ, страница 3

4. Аппроксимация контура (при необходимости). Аппроксимация - это представление сложного геометрического элемента участками более простых геометрических элементов. Например, линейная аппроксимация дуги окружности - это замена её участками прямых линий. Необходимость выполнения аппроксимации определяется типом интерполятора имеющегося в системе управления данного оборудования. Интерполятор - это устройство, которое обеспечивает перемещение инструмента относительно детали из одной опорной точки в другую в соответствии с законом, заложенным в него. Интерполяторы бывают линейными или линейно-круговыми. Если интерполятор линейный, весь контур детали, а, следовательно, и эквидистанту, необходимо представить только участками прямых линий. Расчёт координат промежуточных опорных точек выполнится с учётом радиуса дуги и допуском на аппроксимацию, который может составлять одну треть от допуска на обработку. Если интерполятор линейно-круговой, траектория движения инструмента может включать как участки прямых линий, так и дуги окружностей.

18

Пример аппроксимация дуги участками прямых линий (рис. 2.3.). При наличие в системе управления только линейного интерполятора, криволинейные участки обрабатываемого контура, в частности дуги окружностей, приходится аппроксимировать участками прямых линий. В этом случае можно использовать следующие рекомендации.

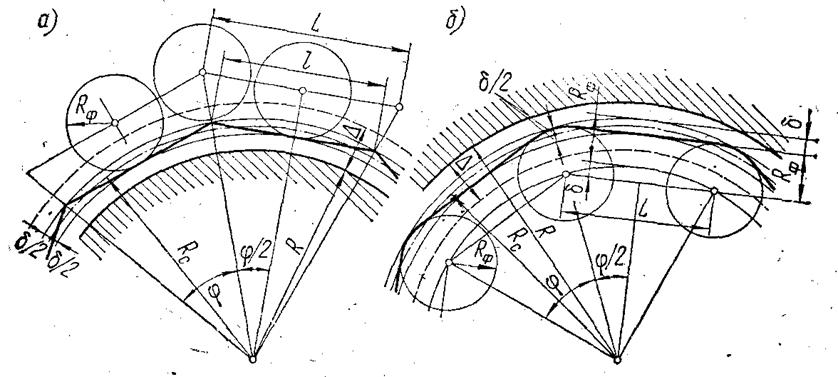
Рис.  2.3. Аппроксимация контура окружности ломаной ли­нией и построение траектории движения инструмента при фрезеровании выпуклого (а) и вогнутого (б) контуров.

     Промежуточные опорные точки на дуге определяются для каждого отрезка ломаной линии, которой аппроксимируется дуга окружности. При фрезеровании плоского контура, очерченного дугами окружностей, можно выделить два характерных случая: обработка выпуклого контура (рис.  2.3. а) и обработка вогнутого контура  (рис. 2.3 б). Контур имеет номинальный радиус R при одностороннем расположении поля допуска. При обработке  выпуклого контура траектория движения центра фрезы выбирается такой, при которой фреза формирует поверхность с размером, соответствующим середине поля допуска Δ на обработку. Величина этого среднего размера   R_c = R +Δ/2. Так как допуск на аппроксимацию не должен превышать величины δ= (0,1—0,3)Δ, то заменяющая ломаная линия должна уложиться в круговую полосу шириной  ± δ/2 (от радиуса R_c  - δ/2 до радиуса R_c  + δ/2). Как следует из рис. 2.3 а, в этом случае косинус половины центрального угла одного звена ломаной линии равен:

19

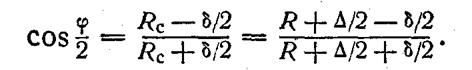
Тогда длина одного звена ломаной линии на обработанной поверхности (величина огранки) определится так:

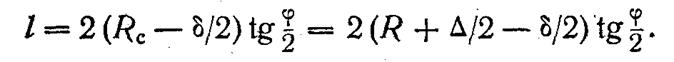
Соответственно длина одного звена ломаной траектории центра фрезы (расстояние между соседними опорными точками) будет равна:

где R_ф—радиус фрезы.

При обработке вогнутого контура с номинальным радиусом R,  в случае одностороннего расположения поля допуска Δ (см. рис. 2.3 б) радиус фрезы R_ф  должен быть меньше радиуса обрабатываемого контура. При условиях, аналогичных тем, которые были приняты в предыдущем случае, косинус половины центрального угла одного звена ломаной траектории движения центра фрезы определяется по формуле:

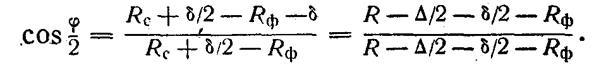
Длина звена ломаной траектории фрезы

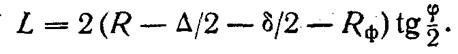
5. Заполнение расчётных таблиц. Следует иметь в виду, что координаты опорных точек, рассчитанные для записи управляющей программы, могут отображаться в абсолютной системе отсчёта, когда все размеры задаются от одной, единой базы, или в относительной системе отсчёта, когда следующая опорная точка задаётся от предыдущей опорной точки, (эта система записи координат называется иногда «запись по приращениям»). Примеры представления размеров в абсолютной и в относительной системе координат показаны на рис. 2.4. 

20

Рис. 2.4. Примеры представления размеров детали:

                        а) в абсолютной системе координат;

                        б) в относительной системе координат (по приращению).

В процессе расчёта опорных точек накапливается большой объём информации: координаты опорных точек, рассчитанные в абсолютной системе отсчёта (Таблица 2.1), а, при необходимости, пересчитанные в относительную систему отсчёта (Таблица 2.2);  координаты центра окружностей (Таблица 2.3); параметры круговой интерполяции I, G, K (Таблица 2.4) и т. п.  Для лучшей организации этой информации, вся она заносится в таблицы, примеры которых представлены ниже. 

(Таблица 2.1)

Координаты опорных точек на эквидистанте

в абсолютной системе отсчёта.

Опорная точка	X	Y	Опорная точка	X	Y
О	0	0	9	229	120
Твх.	-9	130	10	206,75	91,8
1	-9	145	11	117,67	79,73
2	25	179	12	111,91	75,88
3	54,2	162,42	13	79,41	15,88
4	54,92	161,94	14	60	6
5	182,78	143,67	15	37,7	21,13
6	182,92	143,66	16	-6,59	132,43
7	183,49	143,84	17	-9	145
8	200	149	Твых. = 18	-9	160

21

(Таблица 2.2)

Координаты опорных точек на эквидистанте  в относительной системе отсчёта, т.е. координаты i-ой точки, относительно  (i-1)-ой.