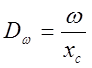 [1/c],
[1/c], 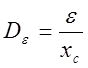 [1/c2],
[1/c2],
где Dw - добротность по угловой скорости,
De - добротность по ускорению,
Хс – погрешность исполнения добротности, скоростная ошибка, показывающая разницу между фактической и желаемой величинами при вращении исполнительного механизма.
Желаемая ЛАЧХ базируется на этих добротностях, если они не соблюдаются, ЖЛАЧХ быть не может;
3. находится частота wк=Dw;
4. через wк проводится прямая 1 с наклоном –20 дБ/дек;
5. находится частота wl=De;
6. через wl проводится прямая 2 с наклоном –40 дБ/дек (если требуется большой запас по амплитуде в рабочем диапазоне) или –60 дБ/дек (если запас требуется меньше или с целью удешевления системы);
7. находится точка пересечения прямых 1 и 2, которая соответствует частоте w1;
8. по методике Солодовникова находится wс;
9. через wс проводится прямая 3 с наклоном –20 дБ/дек;
10. на пересечении прямых 2 и 3 находится точка, соответствующая частоте w2;
11. задаем частоту w3, на уровне нижней частоты рабочего диапазона ЛСУ, соответствующем запасу устойчивости ЛСУ по амплитуде;
12. для частоты w>wс ЛАЧХ считается высокочастотной и совпадает с исходной ЛАЧХ разомкнутой ЛСУ;
13. графически производится вычитание Lж-Lисх для нахождения передаточной функции корректирующего устройства.
Пути реализации корректирующего устройства:
- физический путь – с помощью схем R-L-C – цепочек;
- программный путь за счет микропроцессора.
Суть программного пути в том, чтобы увеличивать или уменьшать входное напряжение на исполнительном органе в зависимости от режима его работы.
ВЫБОР ЗВЕНЬЕВ ЛСУ
Объекты регулирования
Объект регулирования (ОР) как правило задается в техническом задании. Это тот объект, выходные параметры которого составляют предмет управления.
Выбор производится с учетом:
- математической модели,
- критериев 1-8,
- специфических требований.
Существует два пути получения математической модели:
1. теоретический поиск дифференциального уравнения – привлекая аппарат курсов ТАУ, МОТС, МСУ, специалист предметной области теоретическим путем, исходя из физики работы объекта, составляет его дифференциальное уравнение, линеаризует его и определяет взаимосвязь физических параметров ОР с коэффициентами уравнения;
2. экспериментальный – используется практически для все сложных объектов, на вход объекта подается 1(t), d(t), sin(t) – эти воздействия желательно подавать поочередно, комбинированно с целью уточнения передаточной функции; после получения экспериментальных переходных характеристик находится передаточная функция. Недостаток этого пути – не всегда возможно реализовать эксперимент.
Для всех объектов: 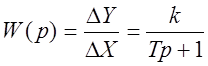 ,
,
где DY=Y-Y0 – отклонение выходного параметра от режимного значения,
DХ=Х-Х0 – отклонение входного параметра от режимного значения,
k – коэффициент передачи на участке, окружающем по диапазону параметров режимную точку,
Т – постоянная времени.
Коэффициент k вычисляется как правило по предельным значениям входной и выходной величин:
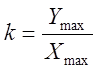 .
.
Т практически находится
из кривой переходного процесса как 1/3 времени переходного процесса: 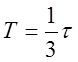 .
.
![]()

![]()
![]()
 Т
Т
t
1. Дизель – входная величина Х=L(t) – перемещение топливной рейки, дозирующей топливо в камеру сгорания, выходная величина Y=w(t) – угловая скорость вала двигателя.
Введем обозначения: 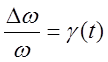 ,
, 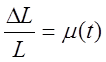 ,
тогда получим уравнение:
,
тогда получим уравнение:
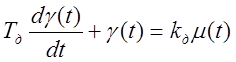 .
.
n – число камер сгорания, тогда 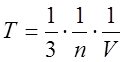 ;
;
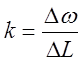 .
.
Для автомобиля Жигули: n=4, V=0,4, 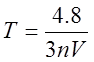 ,
,
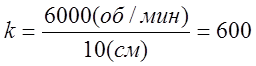 ,
,
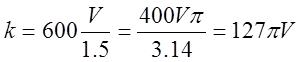 .
.
2. 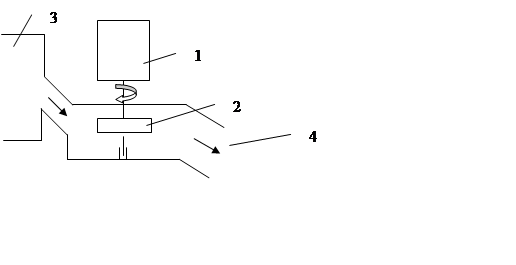 Гидротурбина
Гидротурбина
Вода, перетекая из верхнего бьефа (3) в нижний бьеф (4), вращает лопасти турбины (2), на одной оси с которой установлен электрогенератор (1). Поток воды регулируется так называемым направляющим аппаратом НА, который представляет из себя металлические лопатки типа жалюзи. НА регулируется гидроприводом.
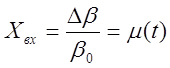 ,
,
где b - угол открытия лопаток НА.
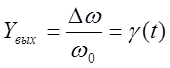 ,
,
где w - скорость вращения гидротурбины и генератора.
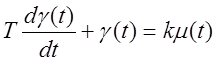 .
.
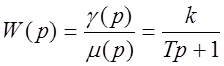 .
.
С открытием лопаток НА приращение Dw остается постоянным, а ток возрастает.
Для Саратовской ГЭС:
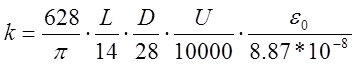 ;
;
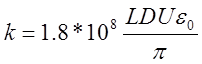 .
.
где L – перепад, м;
D – диаметр турбины, м;
U – напряжение возбуждения в обмотке, В.
В момент открытия лопаток НА турбина набирает
максимальное число оборотов за время переходного процесса ![]() с, отсюда найдем постоянную времени:
Т=1/3t=100 с.
с, отсюда найдем постоянную времени:
Т=1/3t=100 с.
Для любой ГЭС:
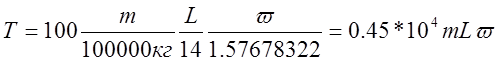 ,
,
где 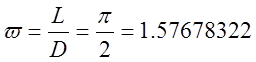 - число Власова.
- число Власова.
Эти примеры относились к так называемым односвязным объектам, то есть к объектам, у которых регулируется одна выходная координата по одной входной. В реальной ситуации объекты как правило бывают многосвязными, когда а выходную координату могут действовать несколько входных. Причем существует корреляционная связь между водными воздействиями. Та связь проявляется таким образом, что выходная координата определяется параметрами входных воздействий в каждый момент времени.
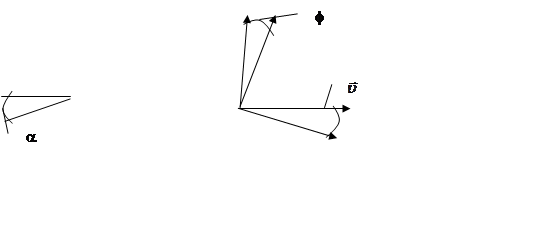 3. Самолет
3. Самолет


![]() - скорость;
- скорость;
![]() - тонгаж;
- тонгаж;
![]() - высота;
- высота;
![]() - курс.
- курс.
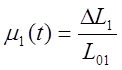 ,
, 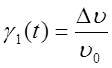 ,
,
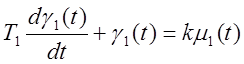 .
.
DL1 – перемещение топливной заслонки около положения L01.
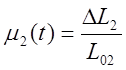
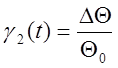
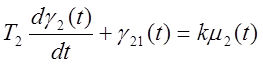
DL2 – перемещение руля курса вокруг положения L01.
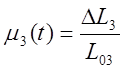
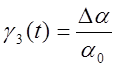
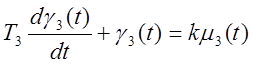
DL3 – перемещение руля высоты.
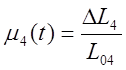
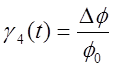
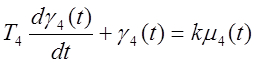
DL4 – перемещение руля тонгажа.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.