Методичні вказівки та контрольні завдання з дисципліни “Будівельна механіка (спецкурс)”. Частина 2 (Статично невизначні системи), страница 4

Важливо засвоїти зміст коефіцієнтів та вільних членів канонічних рівнянь методу переміщень і звернути увагу на їх знаки й виконання умови , згідно з теоремою про взаємність реакцій. Основна система у методі переміщень, на відміну від методу сил, завжди вибирається, як правило, однозначно: у жорстких вузлах системи накладають в’язі, які перешкоджають кутовим переміщенням, але не перешкоджають лінійним, а у вузлах, що мають лінійні переміщення, накладають в’язі, які перешкоджають лінійним переміщенням, але не перешкоджають кутовим.

Рівняння методу переміщень можна складати у двох формах: канонічній або розгорнутій (у формі основних і додаткових рівнянь).

Коефіцієнти та вільні члени канонічних рівнянь визначаються за допомогою статичного методу або шляхом перемноження епюр. При складанні рівнянь у розгорнутій формі використовуються формули для значень реакцій у кінцевих перерізах окремих стрижнів основної системи від кінематичних, силових й інших впливів (див. додатки А і Б). При визначенні коефіцієнтів і вільних членів канонічних рівнянь обов’язково виконується їх перевірка з використанням умови , згідно з теоремою про взаємність реакцій, а також шляхом перемноження епюр. Для симетричних систем значних спрощень можна досягти, враховуючи їх симетрію.

      При розрахунку статично невизначних систем на дію температури і переміщення опор специфічним є лише знаходження  вільних членів канонічних рівнянь.

      Епюри внутрішніх зусиль для заданої статично невизначної системи при використанні канонічної форми методу переміщень будуються на основі принципу незалежності дії основних невідомих, заданого навантаження та інших впливів. Так, епюра згинальних моментів від заданого навантаження будується за формулою

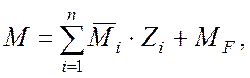                                                        (2)

      де       – епюра згинальних моментів в основній системі від

                – епюра згинальних моментів в основній системі від заданого навантаження або інших впливів;

           n    – ступінь кінематичної невизначності системи.

      Побудову епюр M, Q і N для заданої системи зручно виконувати за таким алгоритмом:

1.  За допомогою формули (2) обчислюються згинальні моменти в кінцевих перерізах кожного стрижня заданої системи.

2.  У подальшому виконуються пункти алгоритму (2 і 3), які вказані в алгоритмі для методу сил.

      Після побудови епюр внутрішніх зусиль, необхідно виконати їх статичну й кінематичну перевірки.

          Епюри внутрішніх зусиль (M, Qі N) для заданої системи при використанні розгорнутої форми методу переміщень будуються на основі принципу незалежності дії основних невідомих, заданого навантаження або інших впливів за таким алгоритмом:

1.  Значення згинальних моментів та поперечних сил у кінцевих перерізах окремих стрижнів від основних невідомих (φ і δ), зовнішнього навантаження й інших впливів визначаються з використанням формул, указаних у додатках А і Б.

2.  У подальшому виконується пункт 2 алгоритму, який указаний в алгоритмі для канонічної форми методу переміщень.

      При  розрахунках рам із використанням обчислювальної техніки зручною буде матрична форма методу переміщень.

Питання та завдання для самоконтролю

1  Як підрахувати ступінь кінематичної невизначності системи?

2  В чому полягає ідея методу переміщень? Основні невідомі методу переміщень.

3  Що таке основна система методу переміщень та її утворення?

4  Канонічна та розгорнута форма рівнянь методу переміщень.

5  Зміст канонічних рівнянь і окремих їх елементів.

6  Як обчислюються коефіцієнти матриці жорсткості та вектора вільних членів?

7  Як виконується перевірка коефіцієнтів матриці жорсткості і вектора вільних членів канонічних рівнянь?

8  Як будуються епюри внутрішніх зусиль при використанні канонічної та розгорнутої форм методу переміщень?

9  Виконання перевірок епюр внутрішніх зусиль.

10  Урахування симетрії системи.

11  Використання групових невідомих.

12  Особливості розрахунку статично невизначних систем на зміну температури та зміщення опор.

13  Сформулюйте пункти алгоритму розрахунку СНС методом переміщень.

ЛІТЕРАТУРА

Основна

1 Смирнов А.Ф., Александров А.В., Лащеников Б.Я., Шапошников Н.Н. Строительная механика стержневых систем. - М.: Стройиздат, 1981. - 512 с.

2  Дарков А.В., Шапошников Н.Н. Строительная механика. - 8-е изд., перераб. и доп. – М.: Высш. школа, 1986. – 544 с.

3  Киселев В.А. Строительная механика, общий курс – 4-е изд., исправленное и доп. – М.: Стройиздат, 1986. – 520 с.

4  Бутенко Ю.И., Кан С.Н., Пустовойтов В.П. и др. Строительная механика стержневых систем и оболочек. - К.: Вища школа, 1980. - 488 с.

5  Доценко И.С. Строительная механика. – К.: Вища школа, 1976. - 296 с.

Допоміжна

6  Строительная механика. Руководство к практическим занятиям / Под ред. Ю.И. Бутенко. - К.: Вища школа, 1989. - 367 с.

8  Ржаницин А.Р. Строительная механика. - М.: Высшая школа, 1982. - 400 с. (2-е  изд.,  перераб.  и доп., 1991. - 439 с.)

9  Руководство к практическим занятиям по курсу строительной механики (статически определимые и неопределимые системы) / Под ред.    Г.К. Клейна. - 3-е изд., перераб. и доп. - М.: Высшая школа, 1973. - 360 с.

Додаток А

Формули для розрахунку стрижневих систем на міцність методом переміщень у розгорнутій формі

Стрижень із защемленим і шарнірно опертим кінцями

 

                     

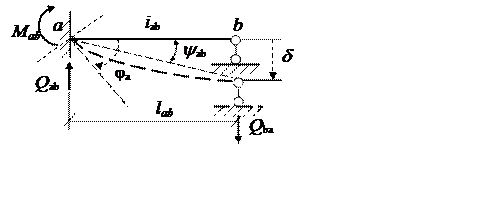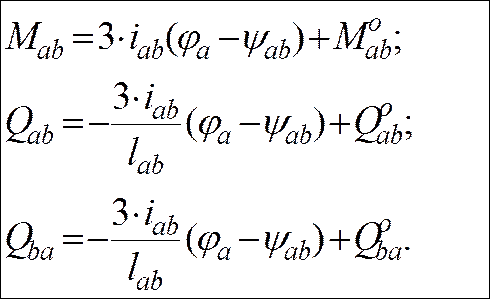
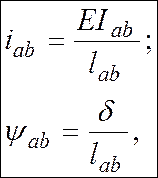
де – моменти і поперечні сили в указаних перерізах основної системи методу переміщень від зовнішнього навантаження або інших впливів (див. додаток Б), урахованих із відповідним знаком.

Стрижень із двома защемленими кінцями