Канонічне рівняння методу сил
записується так: ![]() ,
,
де ![]() – основне невідоме
методу сил (в арці без затяжки – це величина розпору, а в арці із затяжкою – це
зусилля в затяжці);
– основне невідоме
методу сил (в арці без затяжки – це величина розпору, а в арці із затяжкою – це
зусилля в затяжці);
![]() –
переміщення перерізу, де прикладена (прикладені)
–
переміщення перерізу, де прикладена (прикладені)![]() ,
у напрямку
,
у напрямку ![]() , від
, від ![]() ;
;
![]() –
переміщення перерізу, де прикладена (прикладені)
–
переміщення перерізу, де прикладена (прикладені)![]() ,
у напрямку
,
у напрямку ![]() , від зовнішнього навантаження або
інших впливів.
, від зовнішнього навантаження або
інших впливів.
Значення ![]() обчислюється
за формулою
обчислюється
за формулою
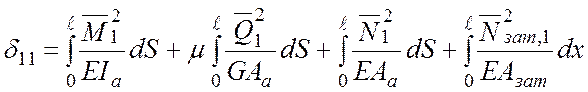 ,
,
де ![]() –
внутрішні зусилля в арці та затяжці від
–
внутрішні зусилля в арці та затяжці від ![]() ;
;
![]() – коефіцієнт, що враховує форму
поперечного перерізу арки;
– коефіцієнт, що враховує форму
поперечного перерізу арки;
![]() –
відповідні жорсткості арки та затяжки.
–
відповідні жорсткості арки та затяжки.
При розрахунку двошарнірних арок із
постійними жорсткостями, осі яких окреслені за квадратною параболою, у випадку,
коли можна скористатися спрощеннями, що вказані вище, значення ![]() обчислюється за формулою
обчислюється за формулою
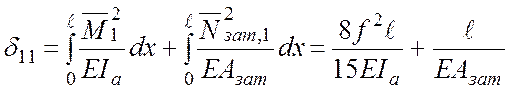 .
.
Для арки без затяжки 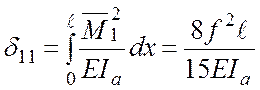 .
.
Значення
![]() обчислюється за формулою
обчислюється за формулою
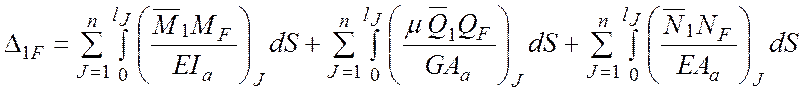 ,
,
де ![]() –
внутрішні зусилля в арці від
–
внутрішні зусилля в арці від ![]() ;
;
![]() –
внутрішні зусилля в арці від зовнішнього навантаження або
інших впливів.
–
внутрішні зусилля в арці від зовнішнього навантаження або
інших впливів.
При розрахунку двошарнірних арок із
постійними жорсткостями, осі яких окреслені за квадратною параболою, у випадку,
коли можна скористатися спрощеннями, що вказані вище, значення ![]() обчислюється за формулою
обчислюється за формулою
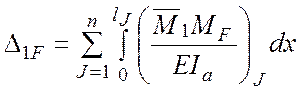 .
.
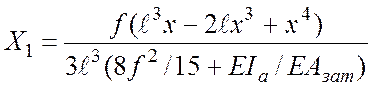 .
.
Для арки без затяжки розпір ![]() обчислюється за умови, що
обчислюється за умови, що![]() .
.
Питання та завдання для самоконтролю
1 Як підрахувати ступінь статичної невизначності системи?
2 В чому полягає ідея методу сил? Основні невідомі методу сил.
3 Що таке основна система методу сил і способи її утворення?
4 Які фактори впливають на вибір раціональної основної системи?
5 Зміст канонічних рівнянь і окремих їх елементів при розрахунку балок, рам, арок та ферм.
6 Які спрощення використовуються при обчисленні коефіцієнтів матриці податливості та вектора вільних членів у розрахунках різних типів стрижневих систем?
7 Як виконується перевірка коефіцієнтів матриці податливості та вектора вільних членів канонічних рівнянь?
8 Як будуються епюри внутрішніх зусиль для різних типів стрижневих систем?
9 Виконання перевірок епюр внутрішніх зусиль.
10 Урахування симетрії системи.
11 Використання групових невідомих.
12 Особливості розрахунку статично невизначних ферм.
13 Особливості розрахунку статично невизначних арок.
14 Особливості обчислення переміщень у статично невизначних системах.
15 Особливості розрахунку статично невизначних систем на зміну температури та зміщення опор.
16 Сформулюйте пункти алгоритму розрахунку СНС методом сил.
Література: /1/ с.319-441; /2/ с.265-302; /3/ с.372-386, 389-390, 397-402; /4/ с.135-150, 152-155; /5/ с.194-216.
Основні поняття та ключові слова розділу: ступінь кінематичної невизначності системи, основна система та основні невідомі, канонічні рівняння, матриця жорсткості, вектор вільних членів.
Ступінь кінематичної невизначності плоских систем. Ідея методу переміщень. Невідомі методу переміщень. Основна система методу переміщень. Канонічні рівняння. Обчислення і перевірка коефіцієнтів та вільних членів канонічних рівнянь. Матриця жорсткості системи й вектор вільних членів канонічних рівнянь. Побудова епюр внутрішніх зусиль (М, Q, N) та їх перевірка. Загальний алгоритм розрахунку статично невизначних систем методом переміщень. Урахування симетрії. Матрична форма методу переміщень. Розрахунок на зміну температури і переміщення опор.
Методичні вказівки
Метод переміщень є одним із основних для розрахунку СНС. Його засвоєння необхідне для розрахунків конструкцій, будівель і споруд та успішного вивчення інших тем курсу. Він покладений в основу методу скінченних елементів.
Важливо навчитися визначати кількість невідомих методу переміщень (ступінь кінематичної невизначності системи).
Деформований стан плоскої стрижньової системи може бути одержаний за допомогою обмеженої кількості параметрів. Такими параметрами є кути повороту жорстких вузлів системи (nв) та лінійні переміщення її вузлів (nл). Кількість кутів повороту дорівнює кількості жорстких вузлів системи, а кількість лінійних переміщень – кількості ступенів свободи умовної шарнірно-стрижньової системи, яка утворюється шляхом розташування шарнірів у всіх жорстких вузлах заданої системи, включаючи й опорні защемлення. Таким чином, ступінь кінематичної невизначності системи (n) дорівнює – n = nв + nл .
За основні
невідомі методу переміщень приймають кутові переміщення жорстких вузлів і
лінійні переміщення вузлів заданої системи, які звичайно позначають ![]() . Кількість невідомих дорівнює
ступеню її кінематичної невизначності (n). У методі переміщень, як і в методі сил, використовується так звана основна
система, яка утворюється із заданої системи “накладанням” у вузлах в’язей,
що перешкоджають переміщенням цих вузлів. Таким чином, основна система методу
переміщень являє собою сукупність взаємозв’язаних стрижнів із різними
закріпленнями їх кінцевих перерізів і є кінематично визначною системою. Для
основної системи можна записати умови її еквівалентності заданій системі на
основі рівнянь рівноваги (статичної сумісності реакцій у “накладених” фіктивних
в’язях при усуненні відмінності основної системи від заданої). Деяка і-та
умова еквівалентності відображає те, що сума реакцій в і-тій
фіктивній в’язі від основних невідомих, зовнішнього навантаження та інших
впливів дорівнює нулю. При цьому використовують принцип незалежності дій та
закон Гука. Як правило, умови еквівалентності записують в канонічній формі і
називають канонічними рівняннями. Кількість канонічних рівнянь дорівнює
ступеню кінематичної невизначності. При розв’язанні цих рівнянь знаходять
основні невідомі – переміщення вузлів заданої системи.
. Кількість невідомих дорівнює
ступеню її кінематичної невизначності (n). У методі переміщень, як і в методі сил, використовується так звана основна
система, яка утворюється із заданої системи “накладанням” у вузлах в’язей,
що перешкоджають переміщенням цих вузлів. Таким чином, основна система методу
переміщень являє собою сукупність взаємозв’язаних стрижнів із різними
закріпленнями їх кінцевих перерізів і є кінематично визначною системою. Для
основної системи можна записати умови її еквівалентності заданій системі на
основі рівнянь рівноваги (статичної сумісності реакцій у “накладених” фіктивних
в’язях при усуненні відмінності основної системи від заданої). Деяка і-та
умова еквівалентності відображає те, що сума реакцій в і-тій
фіктивній в’язі від основних невідомих, зовнішнього навантаження та інших
впливів дорівнює нулю. При цьому використовують принцип незалежності дій та
закон Гука. Як правило, умови еквівалентності записують в канонічній формі і
називають канонічними рівняннями. Кількість канонічних рівнянь дорівнює
ступеню кінематичної невизначності. При розв’язанні цих рівнянь знаходять
основні невідомі – переміщення вузлів заданої системи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.