Методичні вказівки та контрольні завдання з дисципліни “Будівельна механіка (спецкурс)”. Частина 2 (Статично невизначні системи), страница 2

Важливо навчитися визначати кількість невідомих методу сил (ступінь статичної невизначності системи).

      У методі сил використовується система, яка називається основною системою. Вона отримується із заданої системи шляхом відкидання умовно зайвих в’язей і навантаження її зовнішніми силами та зусиллями відкинутих зайвих в’язей. Ці зусилля називають основними невідомими методу сил, які зазвичай позначають . Для основної системи методу сил можна записати умови її еквівалентності заданій системі у формі рівнянь нерозривності переміщень у перерізах, де відкинуті зайві в’язі. Деяка і-та умова еквівалентності відображає те, що переміщення перерізу (перерізів), де прикладена і-та основна невідома в напрямку її дії від основних невідомих, зовнішнього навантаження й інших впливів, дорівнює нулю. Як правило, умови еквівалентності записують у канонічній формі і називаються канонічними рівняннями методу сил. Кількість канонічних рівнянь, як правило, дорівнює ступеню статичної невизначності. При розв’язанні цих рівнянь знаходять основні невідомі.

Важливо засвоїти сутність коефіцієнтів і вільних членів канонічних рівнянь методу сил і звернути увагу на їх знаки та виконання умови , згідно з теоремою про взаємність переміщень. Основна система повинна бути вибрана таким чином, щоб епюри внутрішніх зусиль від одиничних і зовнішніх навантажень були якомога простими й взаємно ортогональними. При цьому рекомендується розглянути декілька варіантів основних систем і, порівнюючи їх, вибрати раціональну.

      Коефіцієнти та вільні члени канонічних рівнянь визначаються за допомогою методу Мора. При цьому інтеграли Мора можна вираховувати відповідно до правила Верещагіна або за формулою Сімпсона-Корноухова. При визначенні коефіцієнтів і вільних членів канонічних рівнянь обов’язково виконується їх перевірка з використанням сумарної епюри внутрішніх зусиль від одиничних навантажень. Для симетричних систем значних спрощень можна досягти, враховуючи їх симетрію.

      При розрахунку статично невизначних систем на дію температури і переміщення опор специфічним є лише знаходження  вільних членів канонічних рівнянь.

      Епюри внутрішніх зусиль для заданої статично невизначної системи будуються на основі принципу незалежності дії основних невідомих, заданого навантаження або інших впливів. Так, епюра згинальних моментів від заданого навантаження будується за формулою

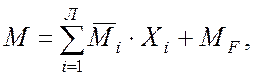                                                        (1)

      де       – епюра згинальних моментів в основній системі від

                – епюра згинальних моментів в основній системі від заданого навантаження або інших впливів;

           Л         – ступінь статичної невизначності системи.

      Побудову епюр M, Q і N для заданої системи зручно виконувати за таким алгоритмом:

1.  За допомогою формули (1) обчислюються згинальні моменти в кінцевих перерізах кожного стрижня заданої системи.

2.  Кожен стрижень системи розглядаємо як балку з шарнірними опорами в кінцевих перерізах, для якої будуються епюри M і Q від зовнішнього навантаження стрижня та моментів, що обчислені в пункті 1. Об’єднавши відповідні епюри M і Q стрижнів системи, отримуємо епюри M і Q для заданої системи.

3.  Епюру поздовжніх зусиль (N) будуємо шляхом використання умов рівноваги окремих вузлів системи.

      Після побудови епюр внутрішніх зусиль необхідно виконати їх статичну й кінематичну перевірки.

      Знаходження переміщень у статично невизначних системах виконується так, як і в статично визначних, із використанням методу Мора. Наприклад, у балках та рамах переміщення, пов’язане зі згином, обчислюється за формулою

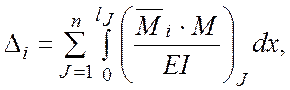
де        – будь-яке лінійне або кутове переміщення;

– функція згинального моменту, яка складена для j-ї ділянки інтегрування у допоміжному (одиничному) стані будь-якої основної системи методу сил;

       – функція згинального моменту, яка складена для j-ї ділянки інтегрування у заданій статично невизначній системі.

      Використання обчислювальної техніки зменшує трудомісткість розрахунку статично невизначних систем методом сил. При цьому найбільш раціональною є матрична форма розв’язання задачі.

2.1 Особливості розрахунку статично невизначних двошарнірних арок

      Різновиди статично невизначних арок. Вибір розрахункової схеми і методу розрахунку. Особливості розрахунку двохшарнірних та безшарнірних арок. Вплив обтиснення на арку (двохшарнірні арки із затяжкою). Поняття про регулювання напружень в арках.

Методичні вказівки

      Вивчаючи цю тему, в першу чергу необхідно звернути увагу на класифікацію арок, вибір основної системи. При розрахунках статично невизначних арок, як правило, використовують метод сил. Особливістю розрахунку арок є врахування при обчисленні переміщень криволінійності осі арки та можливої зміни її жорсткостей у межах прольоту, а також необхідність урахування поперечних і поздовжніх зусиль. Для спрощення розрахунків інколи замінюють криволінійну вісь арки окремими прямолінійними ділянками, кінці яких розташовані на її осі.

      Для статично невизначних арок із затяжкою необхідно проаналізувати вплив податливості затяжки на значення внутрішніх зусиль арки, а також можливість їх зміни шляхом регулювання зусилля у затяжці.

      При розрахунку двошарнірних арок із постійними жорсткостями, осі яких окреслені за квадратною параболою , з початком координат на будь-якій із шарнірних опор,  де   – стріла підйому арки;         – проліт арки, можна використати такі спрощення:

Ø при співвідношенні висоти перерізу арки до її прольоту (), а також  нехтують поперечними та поздовжніми силами при обчисленні коефіцієнта і вільного члена канонічного рівняння методу сил;

Ø коли , тоді інтегрування за довжиною дуги арки, при обчисленні коефіцієнта та вільного члена канонічного рівняння методу сил, замінюється інтегруванням за горизонтальною проекцією осі арки  ().