Министерство общего образования
Российской федерации
Уральский государственный технический университет-УПИ
филиал в г.Краснотурьинске
Кафедра вычислительной техники
Курсовая работа
По численным методам
Решение линейных уравнений методом простой итерации
c помощью программы Microsoft Excel
Руководитель Кузьмина Н.В.
Студент Нигматзянов Т.Р.
Группа М-177Т
2002
Задание.
Тема: «Нахождение с заданной точностью корня уравнения F(x)=0 на промежутке [a;b] методом простой итерации».
Контрольный пример: 0,25-х+sinx=0
Условия задачи: для заданной функции F(x) на интервале [0,5;2] найти корень уравнения F(x)=0 методом простой итерации.
Корень вычислить дважды(с помощью автоматического и ручного расчета).
Предусмотреть построение графика функции на заданном интервале.
Содержание.
Введение 4
1.Теоретическая часть 5
2.Описание хода работы 7
3.Входные и выходные данные 8
Заключение 9
Приложение 10
Библиографический список 12
Введение.
В ходе данной работы мне необходимо ознакомиться с различными методами решения уравнения и найти корень нелинейного уравнения 0,25-х+sin(x)=0 численным методом – методом простой итерации. Для проверки правильности нахождения корня необходимо решить уравнение графически ,найти приближенное значение и сравнить его с полученным результатом.
1.Теоретичесакя часть.
Метод простой итерации.
Итерационный процесс состоит в последовательном уточнении начального приближения х0 (корня уравнения). Каждый такой шаг называется итерацией.
Для использования этого метода исходное нелинейное уравнение записывается в виде: х=j(х), т.е. выделяется х; j(х) – непрерывна и дифференцируема на интервале (а; в). Обычно это можно сделать несколькими способами:
Например:
arcsin(2x+1)-x2=0 (f(x)=0)
Способ 1.
arcsin(2x+1)=x2
sin(arcsin(2x+1))=sin(x2)
2x+1=sin(x2)
x=0.5(sinx2-1) (x=j(x))
Способ 2.
x=x+arcsin(2x+1)-x2 (x=j(x))
Способ 3.
x2=arcsin(2x+1)
x=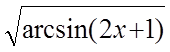 (x=j(x)),знак берется в зависимости от интервала [а;b].
(x=j(x)),знак берется в зависимости от интервала [а;b].
Преобразование должно быть таким, чтобы ½j(x)<1½ для всех принадлежащих интервалу [a;b].В таком случае процесс итерации сходится.
Пусть известно начальное приближение корня x=c0.Подставляя это значение в правую часть уравнения x=j(x),получаем новое приближение корня:c=j(c0).Далее, подставляя каждый раз новое значение корня в x=j(x),получаем последовательность значений
c2=j(c1)
…
cn=j(cn-1) n=1,2,3,…
Процесс итераций следует продолжать до тех пор,пока для двух последовательных приближений не будет выполнено условие: ½cn-cn-1½<e
Решать уравнения численными методами можно с помощью языков программирования, но программа Excel дает возможность справиться сданной задачей более простым способом.
Программа Excel реализует метод простой итерации двумя способами с помощью ручного расчета и с автоматическим контролем точности.
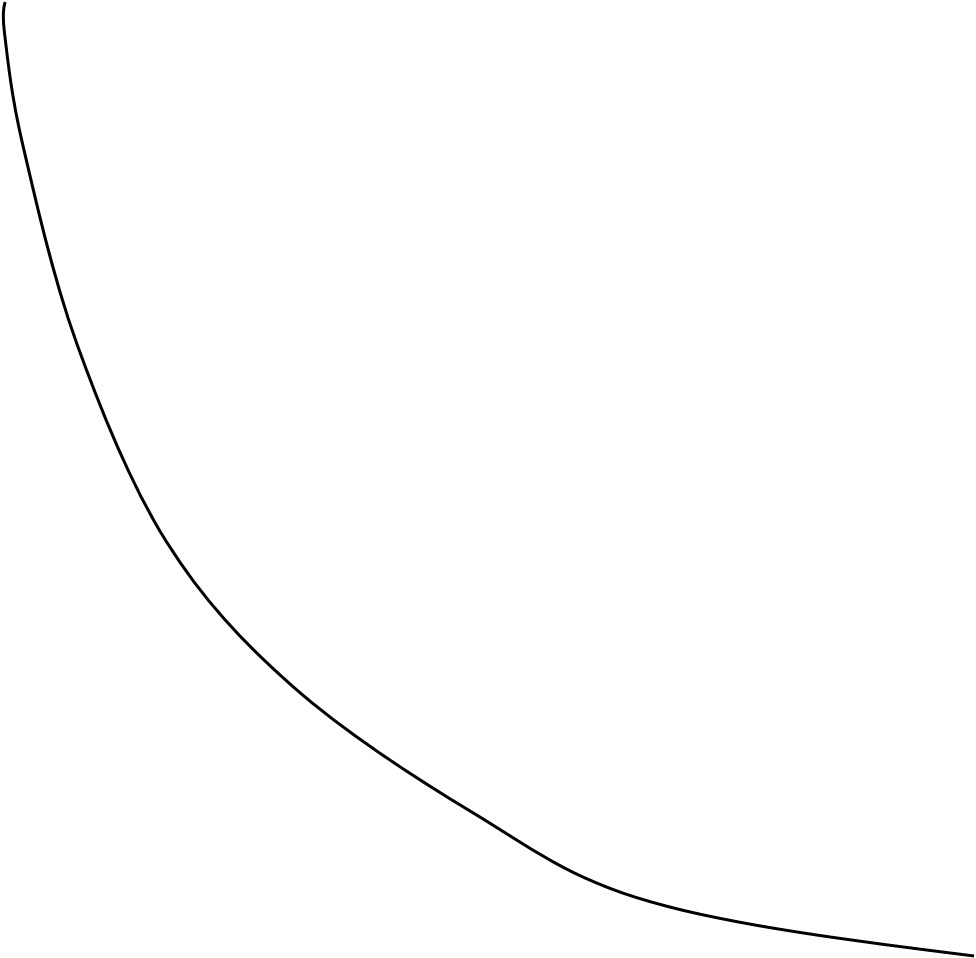
![]()

 у у=х
у у=х
 |


1.
 |
|||
j (с0)
(с0)
 |
|||||||||||||
с0 с2 с4 с6 с8 корень с9 с7 с5 с3 с1
х
|
2.Описание хода работы.
1. Запустил МЕ.
2. Построил график функции y=x и y=0,25+sin(x) на отрезке [0,5;2] с шагом 0,1 назвал лист «График».
3.
Выбрал команду Сервис®Параметры.
Открыл вкладку Вычисления.
Включил режим Вручную.
Отключил флажок Пересчет перед сохранением. Сделал значение поля Пре-дельное
число итераций равным 1,относительную погрешность 0,001.
4. Ввел в ячейку А1 строку «Решение уравнения x=0,25+sin(x) методом простой итерации».
5. Ввел в ячейку А3 текст «Начальное значение»,в ячейку А4 текст «Начальный флаг»,в ячейку В3 значение 0,5 ,в ячейку В4 слово ИСТИНА.
6.
Присвоил ячейкам В3 и В4 имя
«нач_зн» и «нач».
В ячейке В6 будет выполняться проверка,равна ли истина значению ячейки
«нач».Если это так,х будет установлено равным начальному значению, в противоположном
случае равным ячейке В7,т.е. 0,25+синуса х.В ячейке В7 выч-исляется 0,25-синуса
ячейки В6,и тем организуется циклическая ссылка.
7.
В ячейку А6 ввел y=x,и в
ячейку А7 y=0,25+sin(x).В ячейку В6 формулу:
=ЕСЛИ(нач;нач_зн;В7).
В ячейку В7 формулу: y=0,25+sin(B6).
8. В ячейку А9 ввел слово Погрешность.
9. В ячейку В9 ввел формулу: =В7-В6.
10. С помощью команды Формат-Ячейки(вкладка Число) преобразовал ячейку В9 в экспоненциальный формат с двумя цифрами после запятой.
11. Затем организовал вторую циклическую ссылку-для подсчета количества ите-раций.В ячейку А11 ввел текст «Количество итераций».
12. В ячейку В11 ввел формулу: =ЕСЛИ(нач;0;В12+1).
13. В ячейку В12 ввел =В11.
14. Для выполнения расчета установил табличный курсор в ячейку В4 и нажал клавишу F9(Вычислить) для запуска решения задачи.
15. Изменил значение начального флага на ЛОЖЬ,и снова нажал F9.При каждом нажатии F9 выполняется одна итерация и вычисляется следующее приближен-ное значение х.
16.
Нажимал клавишу F9 до
тех пор, пока значение х не достигло необходимой точности.
При автоматическом расчете:
17. Перешел на другой лист.
18. Повторил пункты с 4 по 7,только в ячейку В4 ввел значение ЛОЖЬ.
19. Выбрал команду Сервис®Параметры(вкладка Вычисления).Установил зна-чение поля Предельное число итераций равным 100,относительную погреш-ность равной 0,0000001.Включил ркжим Автоматически.
3.Входные и выходные данные.
Входные:
Начальный флаг ЛОЖЬ.
Начальное значение 0,5
Функция y=0,25-x+sin(x)
Границы интервала [0,5;2]
Точность вычисления при ручном расчете 0,001
при автоматическом ![]()
Выходные:
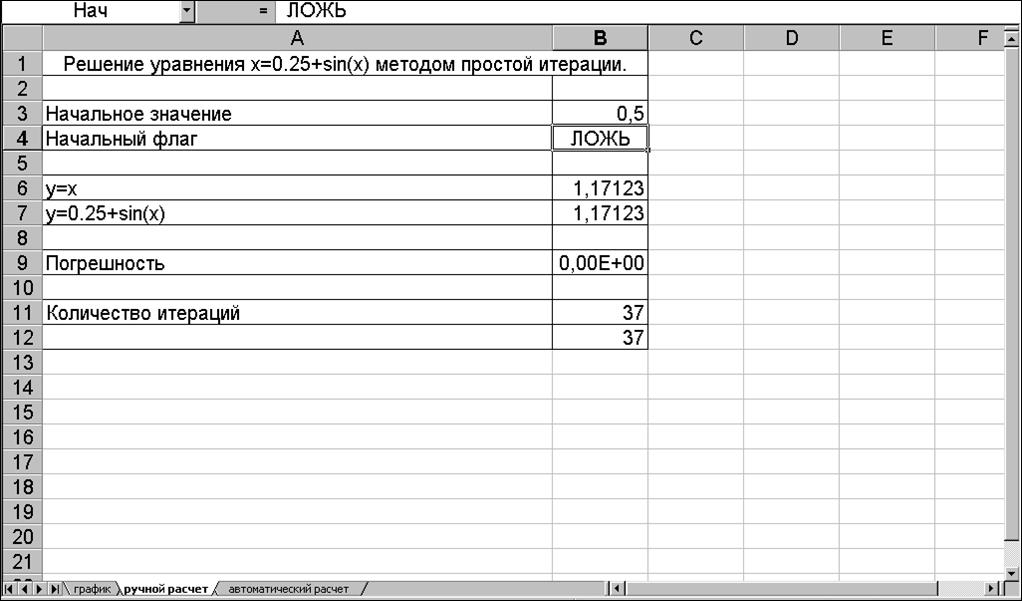
1.
Ручной расчет:
число итераций 37
корень уравнения 1,17123
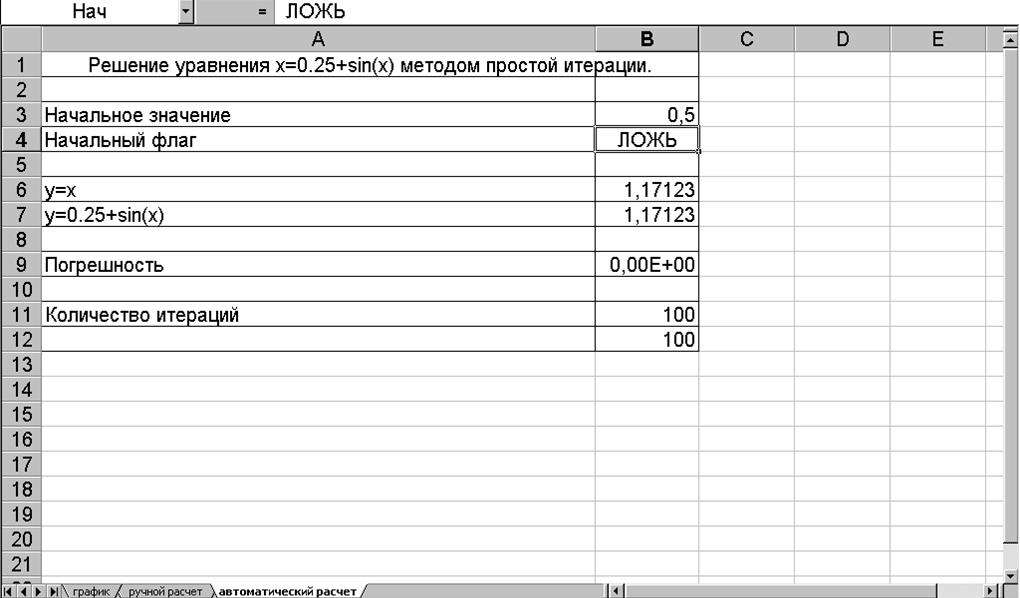
2.
Автоматический расчет:
число итераций 100
корень уравнения 1,17123
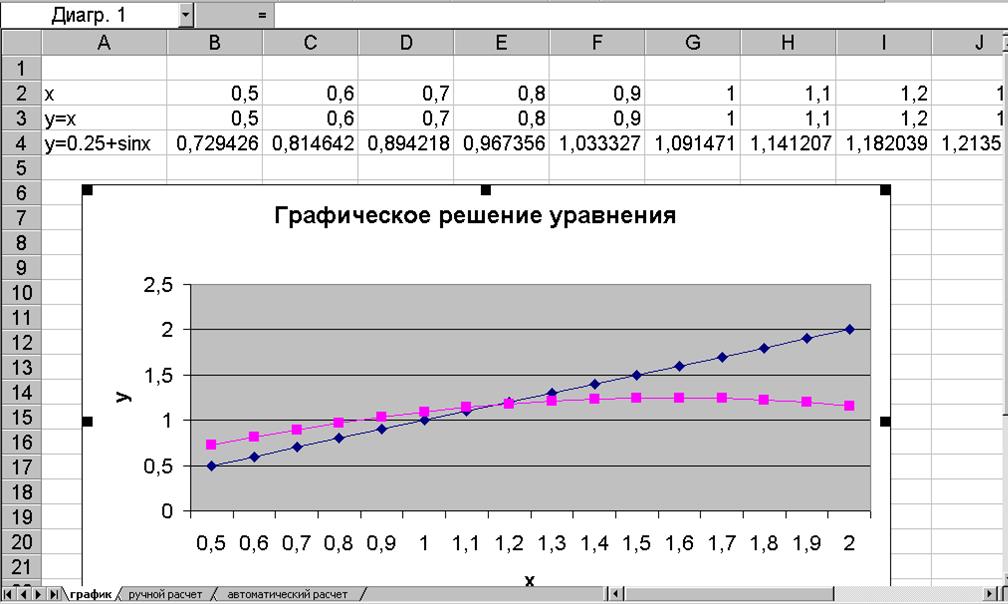
3.
Решение уравнения графическим
способом:
корень уравнения 1,17
Заключение.
В ходе данной курсовой работы я ознакомился с различными методами решения уравнений:
· Графическим методом
· Численным методом
Но так как большинство численных методов решения уравнений являются итерационными, то я на практике использовал этот метод.
Нашел с заданной точностью корень уравнения 0,25-x+sin(x)=0 на промежутке [0,5;2] методом простой итерации.
Приложение.
1.Ручной расчет.
2.Автоматический расчет.
3.Решение уравнения 0.25-x-sin(x)=0 графическим способом.
Библиографический список.
1. Волков Е.А. «Числовые методы».
2. Самарский А.А. «Введение в числовые методы».
3. Игалеткин И.И. «Числовые методы».
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.