Тема: “Линейная аппроксимация табличной функции методом наименьших квадратов”
Контрольный пример:
|
x |
1 |
2 |
6 |
8 |
12 |
17 |
19 |
20 |
23 |
|
y |
15 |
30 |
32 |
38 |
40 |
39 |
33 |
30 |
19 |
Условие задачи:
Аппроксимировать таблично заданную функцию y(x) линейной зависимостью y=kx+b, т.е. найти k и b. Построить график полученной зависимости y=kx+b и нанести на координатную плоскость заданные точки табличной функции. Предусмотреть вывод таблицы заданных значений функции и вычисленных.
введение
1. Теоретическая часть……………………………………………………4
2. описание структуры и программ………………………………….5
3. Входные и выходные данные……………………………………….6
Заключение……………………………………………………………………7
приложение………………..…………………………………………………..8
Список литературы………………………………………………………..17
Тема моей курсовой работы “Приближённое вычисление определённого интеграла методом трапеций”. В данной работе мне необходимо создать меню следующего вида:
Теория
Задание
Контрольный пример
График
Автор
Выход.
Кроме того, написать программу о приближённом вычислении значений определённого интеграла по заданной точности вычисляемого значения и по заданному количеству отрезков разбиения интервала интегрирования. А также построить график подинтегральной функции на заданном интервале.
“Метод трапеций”
Метод трапеций использует линейную интерполяцию, т.е. график функции y=f(x) представляется в виде ломанной, соединяющей точки (xi, yi). В этом случае площадь всей фигуры (криволинейной трапеции) складывается из площадей элементарных прямолинейных трапеций. Площадь каждой такой трапеции равна произведению полусуммы на высоту:
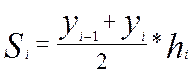 , i=1,2,…,n.
, i=1,2,…,n.
Складывая все эти равенства получаем формулу трапеций для численного интегрирования:

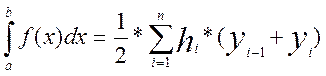
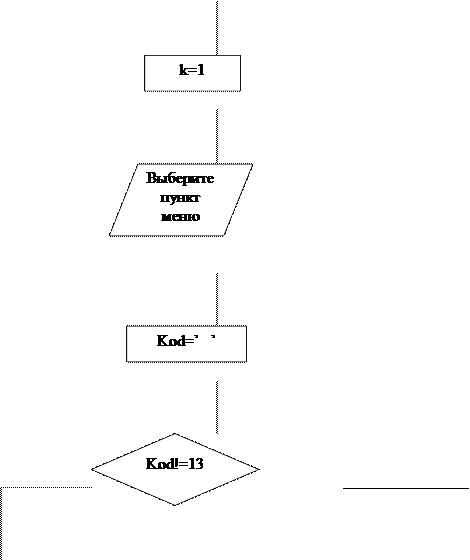
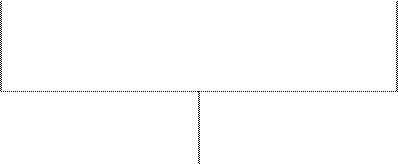
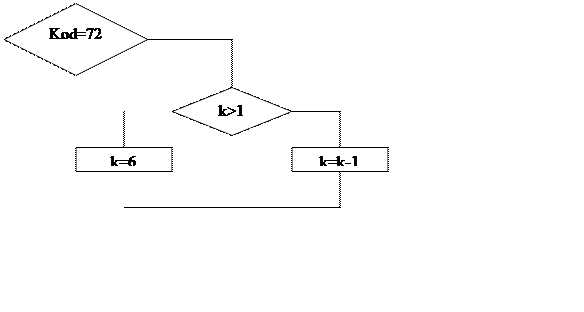
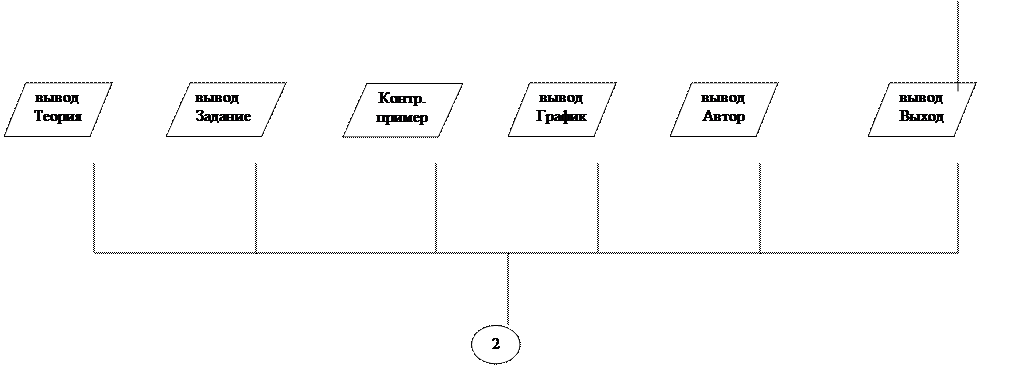
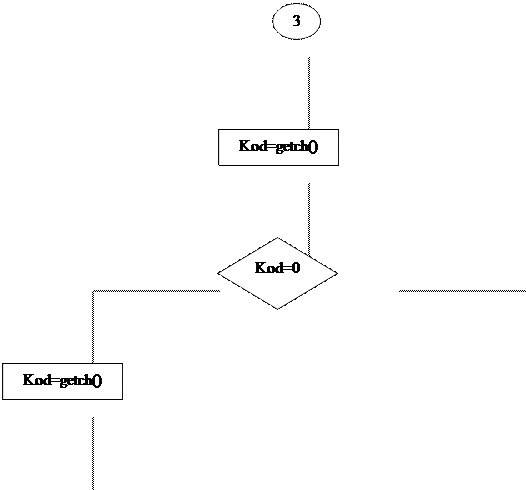
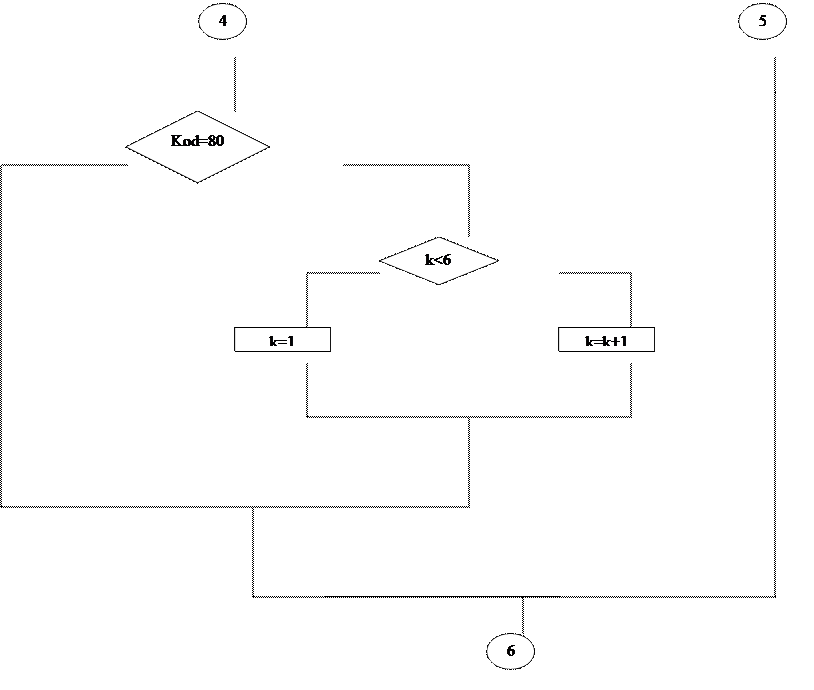
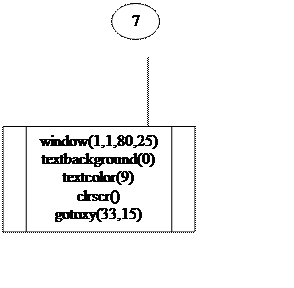
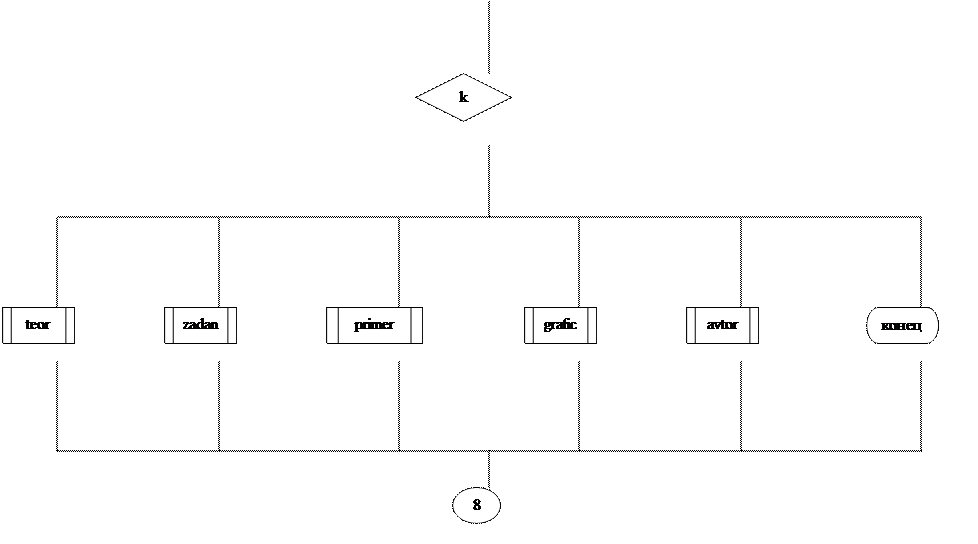
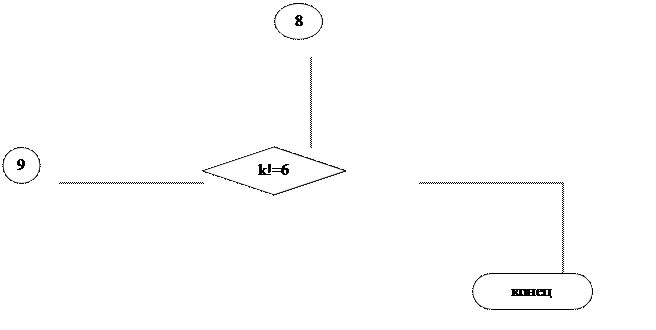
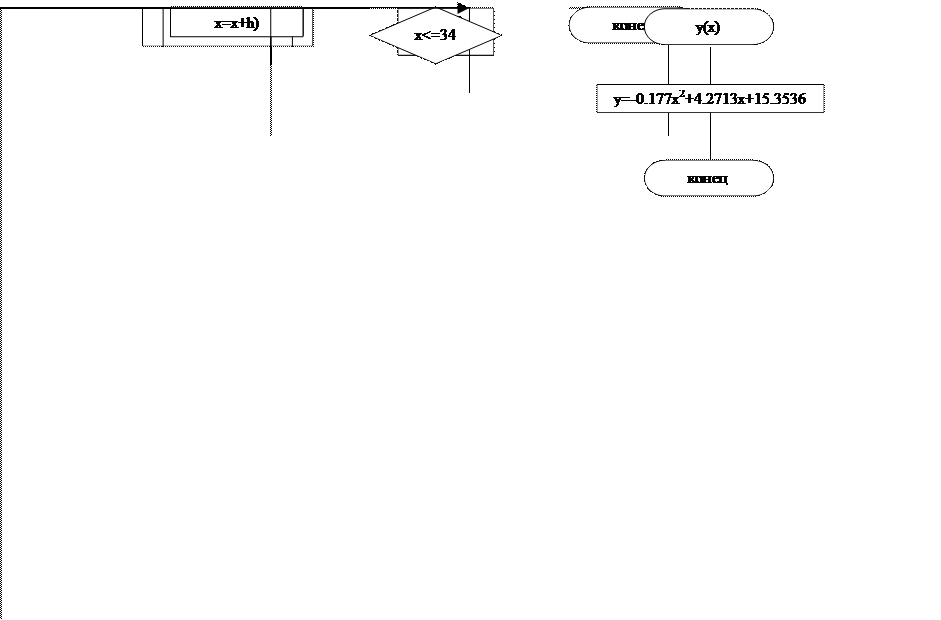
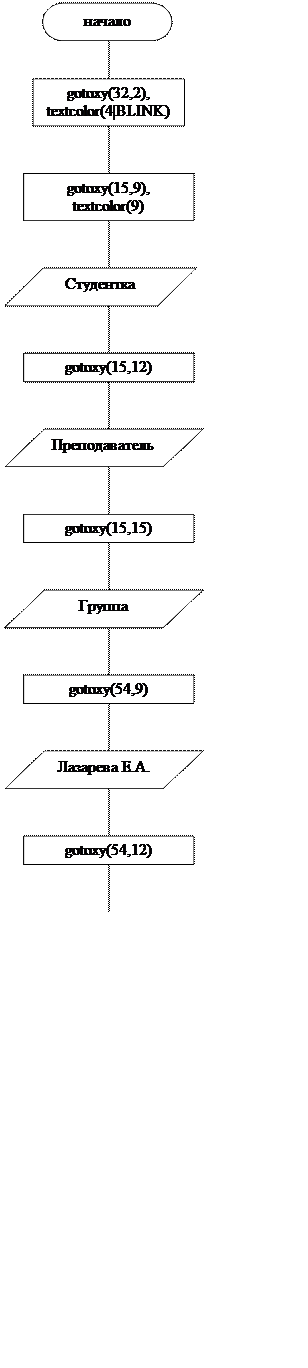
Блок-схема меню
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
 |
|||||||||||||||||||
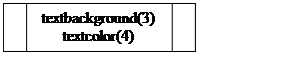 |
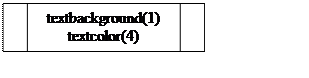 |
||||||||||||||||||
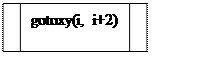 |
|||||||||||||||||||
 |
|||||||||||||||||||
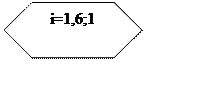 |
 |
|||||||
 |
|||||||
 |
|||||||
 |
|||||||

![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
 |
|||||
 |
|||||
 |
|||||
 |
|||||
 |
|||||
 |
|||||
 |
 |
|||
 |
|||
 |
 |
|||
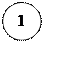 |
|||
 |
|||||||
|
|||||||
|
|||||||
 |
|||||||
 |
|||||
 |
|||||
 |
|||
 |
|||

 |
 |
||
 |
|
 |
 |
 |
 |
 |
 |
|||
 |
|||
 |
|
Входные данные программы Меню |
|
|
mas[6] |
Массив для хранения пунктов меню |
|
k |
Количество пунктов меню |
|
i |
Счетчик пунктов меню |
|
Kod |
Переменная, хранящая код нажатой клавиши |
|
Входные данные пункта «Пример» |
|
|
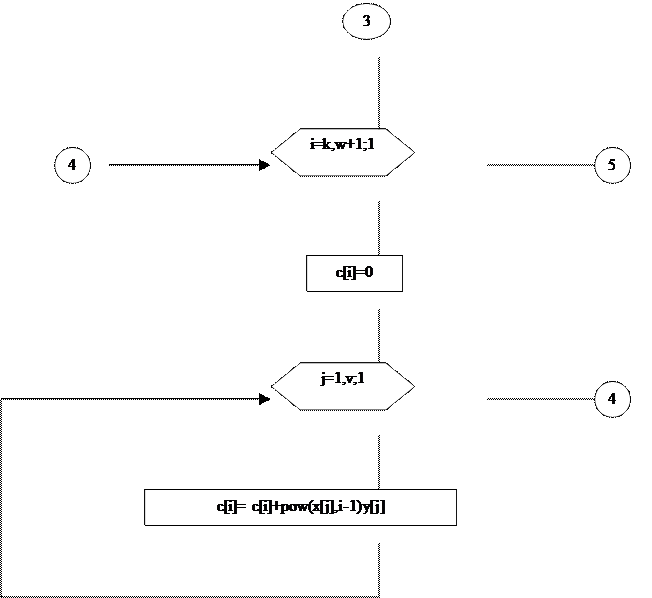
x[10], y[10] |
Массивы независимых переменных и значений таблично заданной функции |
|
b[10][10] |
Массив для хранения коэффициентов при неизвестных a, b, c |
|
c[10] |
Массив для хранения свободных коэффициентов системы |
|
a[10] |
Массив для хранения решений системы, т.е. a, b, c |
|
i, j, f |
Счетчики циклов |
|
n |
Переменная, хранящая количество уравнений системы |
|
w |
Переменная, хранящая степень аппроксимирующей функции |
|
v |
Переменная, хранящая количество заданных точек |
|
p[10] |
Массив для хранения вычисленных значений аппроксимирующей функции |
|
Входные данные для метода Гаусса |
|
|
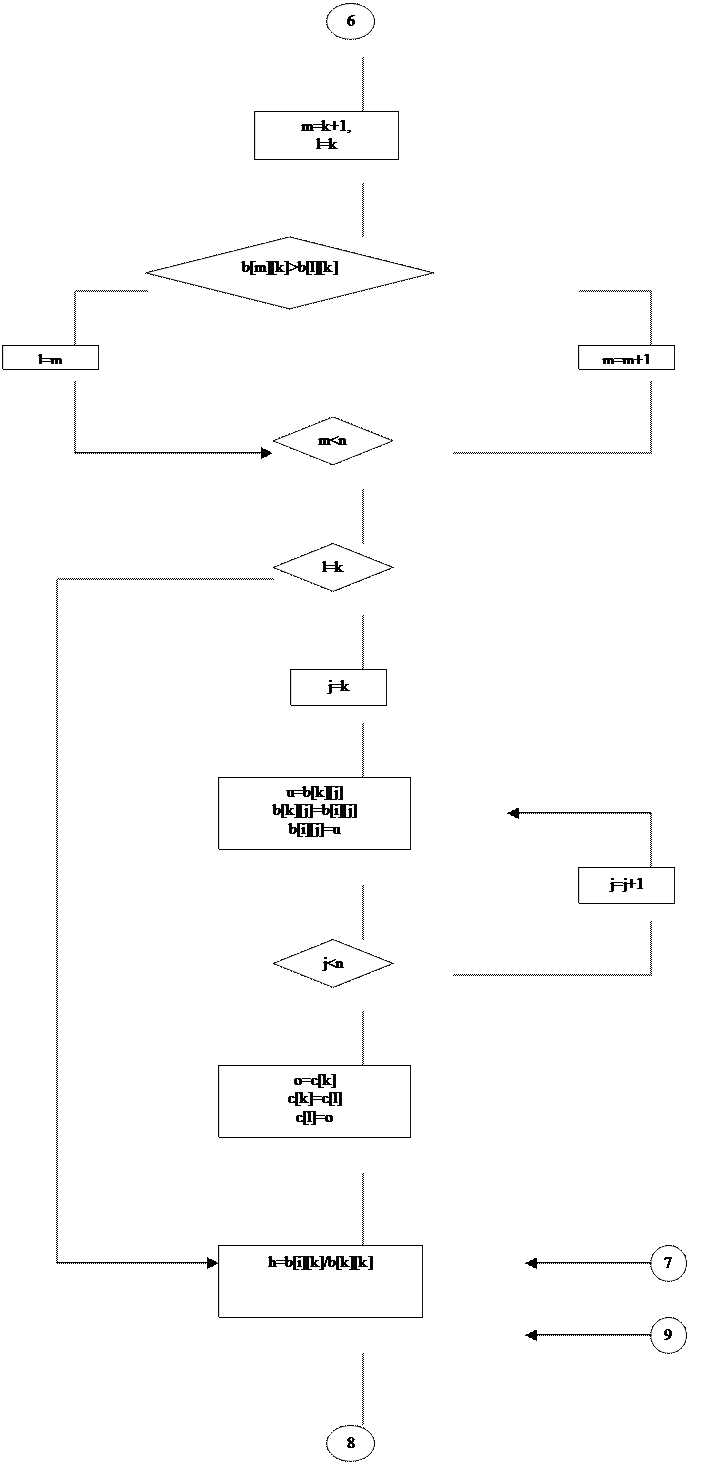
i |
Переменная, хранящая номер уравнения, из которого исключается неизвестное a[k] |
|
j |
Переменная, хранящая номер столбца |
|
k |
Переменная, хранящая номер неизвестного, которое исключается из оставшихся n-k уравнений, а также номер уравнения, с помощью которого исключается a[k] |
|
o |
Переменная, хранящая значение c[k] в перестановке c[k]-c[l] |
|
u |
Переменная, хранящая значение b[k][j] в перестановке b[k][j]-b[i][j] |
|
h |
Переменная, хранящая частное от деления b[i][k]/b[k][k] |
|
s |
Переменная, хранящая сумму произведений вида b[i][j]·a[j] в i-ом уравнении; j-номер столбца |
|
Входные данные для выбора главного элемента в методе Гаусса |
|
|
m |
Переменная, хранящая текущий номер элемента, с которым происходит сравнение |
|
l |
Переменная, хранящая номер наибольшего по модулю элемента системы в столбце с номером k |
|
Входные данные для обратного хода метода Гаусса |
|
|
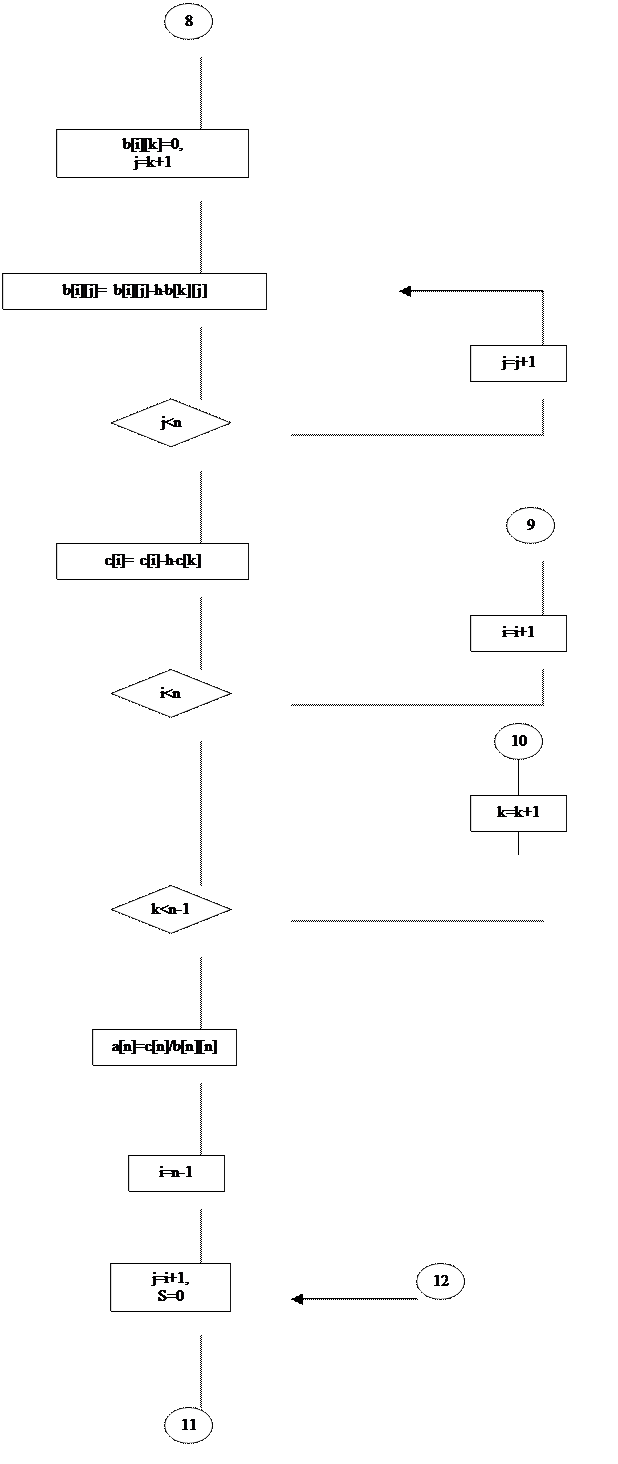
i |
Переменная, хранящая номер неизвестного, которое исключается из i-го уравнения |
|
j |
Переменная, хранящая номер уже науденных неизвестных |
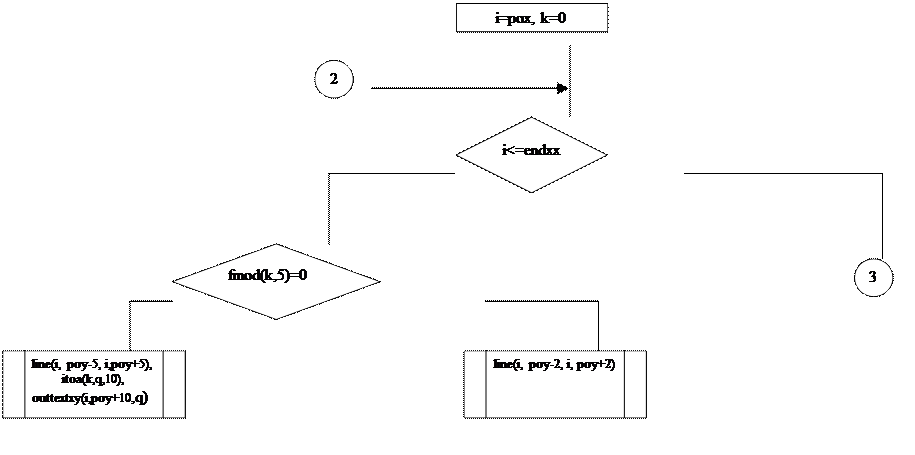
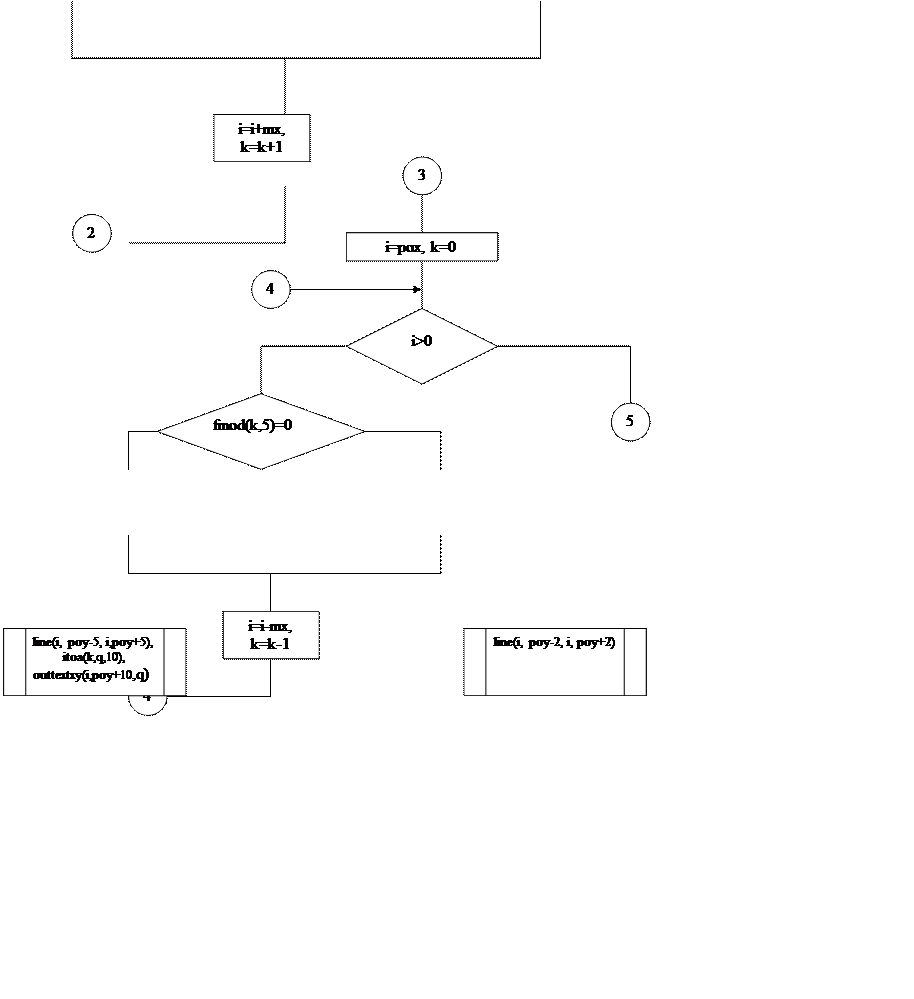
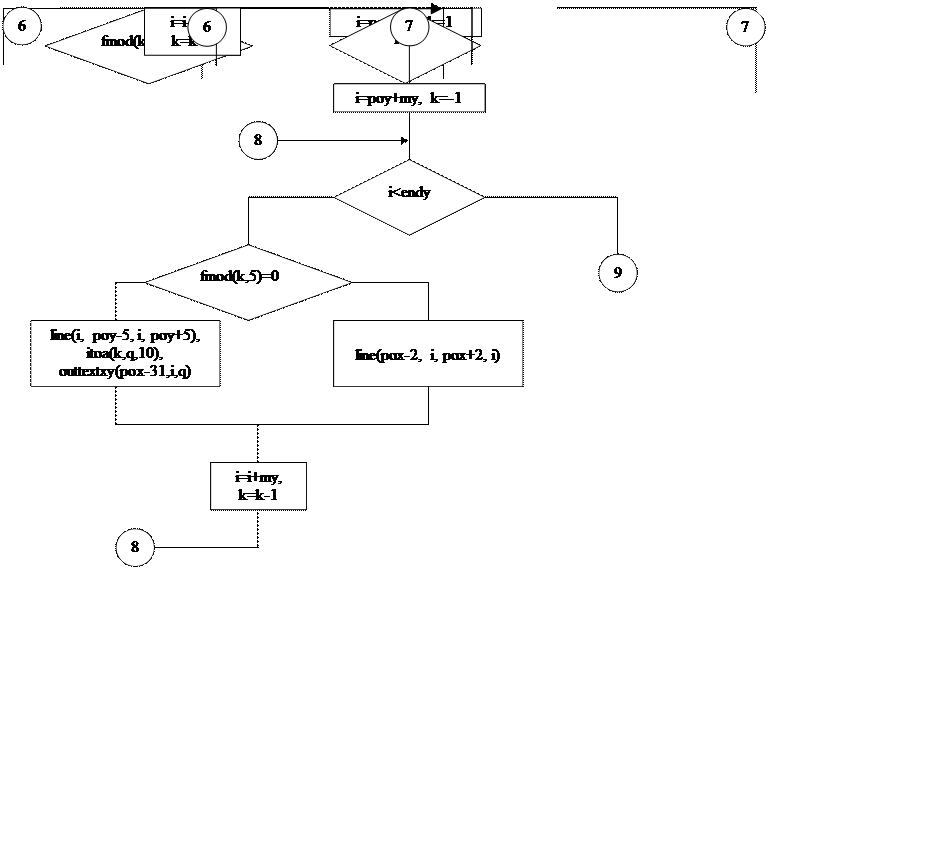
Входные данные пункта «График» |
|
driver |
Переменная для автоматического определения типа видеоадаптера |
mode |
|
endx, endy |
Максимальное разрешение по х и у |
pox, poy |
Координаты пересечения координатных прямых |
mx, my |
Масштаб по х и у соответственно |
kx, ky |
Переменные, хранящие координаты точки c учетом заданного масштаба |
i |
Счетчик циклов; количество разбиений (по полуосям) |
k |
Переменная, хранящая числа для подписей под осями |
h |
Шаг изменения переменной х |
x |
Координата независимой переменной относительно абсолютного окна |
q[25] |
Массив для хранения преобразованного в строку числа |
X[10], Y[10] |
Массивы независимых переменных и значений таблично заданной функции |
y(x) |
Функция для вычисления значения координаты y |
В ходе курсовой работы я изучила метод трапеций и как при помощи него можно вычислять определённый интеграл. Рассмотрела реализацию этого метода на ЭВМ в среде Turbo С.
Кроме того, я научилась организовывать меню. А также поработала со многими функциями текстового и графического режимов среды Turbo С.
Я надеюсь, что данная курсовая работа поможет мне в будущем решать более сложные математические задачи, связанные с численными методами, и реализовывать их на ЭВМ.
Список литературы
1. Демидович Б.П., Марон И.А., Шувалова Э.З. «Численные методы анализа».
2. Иносов В.Л. и др. «Вычислительная техника в инженерных и экономических расчетах».
3. Светозарова Г.И., Сигитов Е.В., Козловский А.В. «Практикум по программированию на алгоритмических языках».
4. Симаков А.Л. Арифметические и логические основы цифровой техники: Конспект лекций. Чебоксары: ЧГУ, 1984, 80с.
5. Турчак Л.И. «Основы численных методов».
6. Под руководством Анисимова Б.В. «Вычислительная техника в инженерных и экономических расчетах».
7. ГОСТ 19.701-90. Схемы алгоритмов, программ данных и систем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.