Содержание:
|
![]() Задание:
Задание:
![]() 1. Теоретическая часть
1. Теоретическая часть
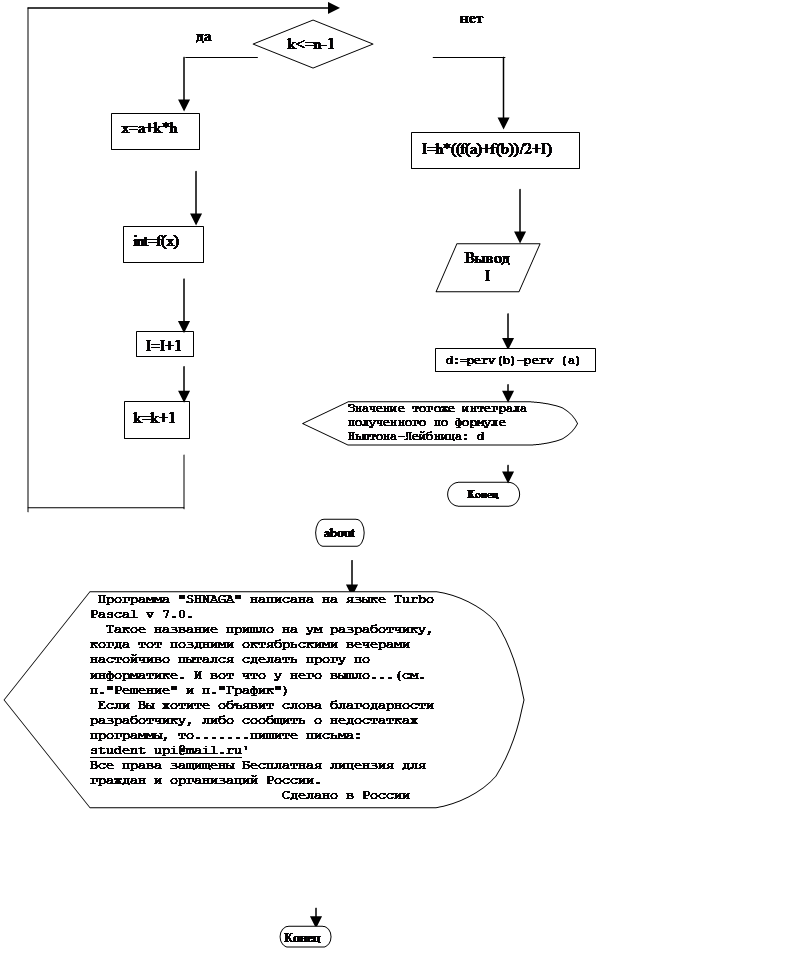
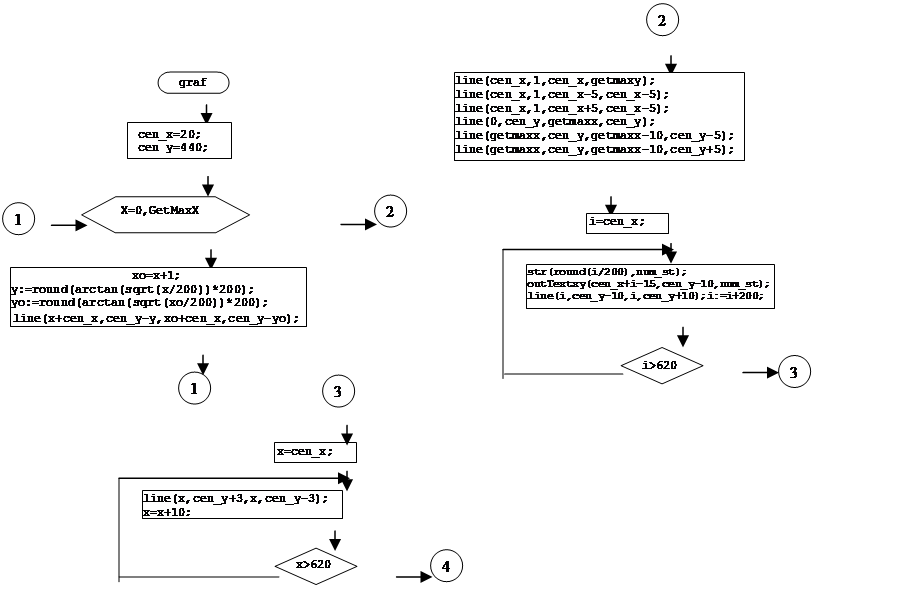
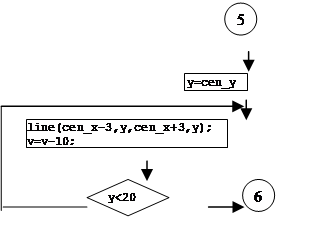
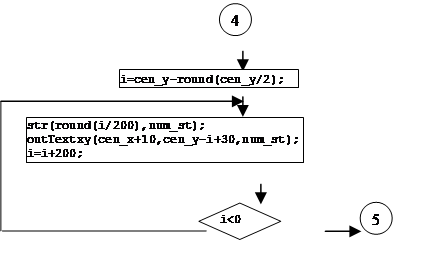
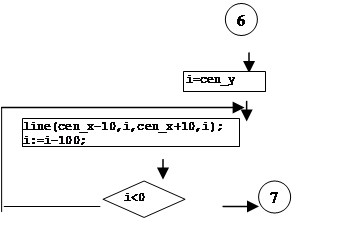
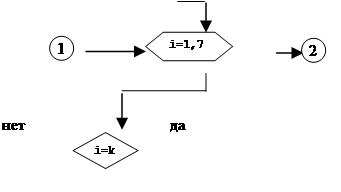
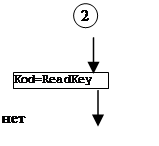
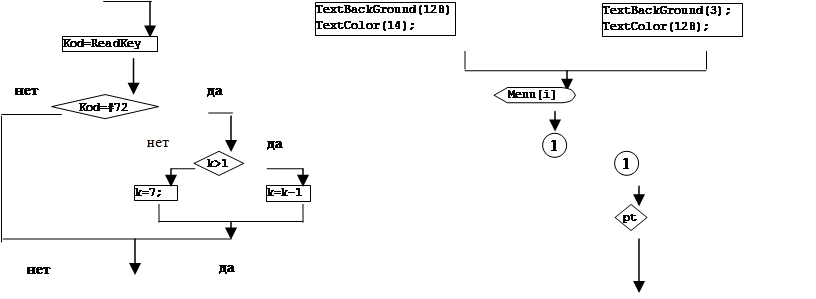
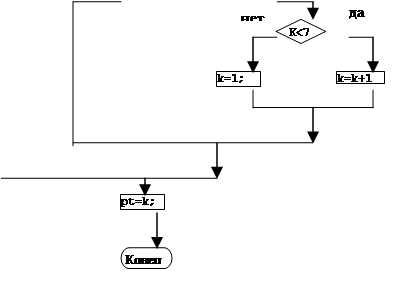
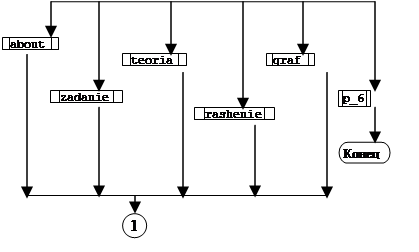
![]() 2. Описание структуры программы (блок-схема)
2. Описание структуры программы (блок-схема)
![]() 3.Входные и выходные данные (какие
переменные используются в структуре и что
обозначают)
3.Входные и выходные данные (какие
переменные используются в структуре и что
обозначают)
![]() Заключение
Заключение
![]() Приложение
Приложение
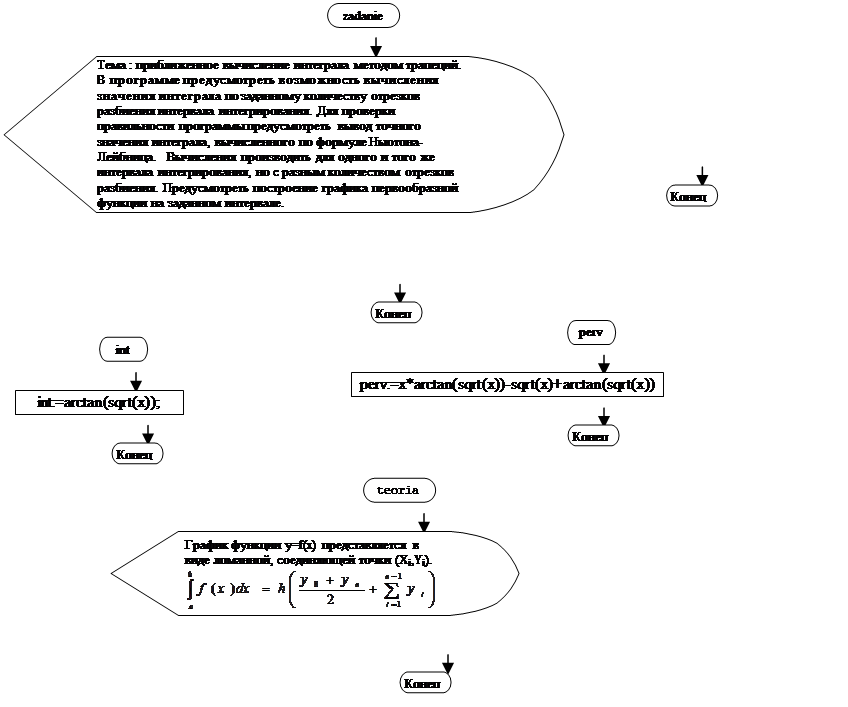
Задание :
Тема: "Приближенное вычисление определенного интеграла методом трапеций"
Контрольный пример:
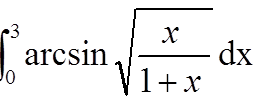 |
|||
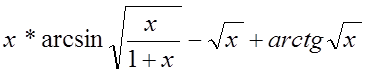 |
|||
Первообразная:
Условие задачи:
В программе предусмотреть возможность вычисления значения интеграла по заданному количеству отрезков разбиения интервала интегрирования. Для проверки правильности программы предусмотреть вывод точного значения интеграла, вычисленного по формуле Ньютона-Лейбница. Вычисления производить для одного и того же интервала интегрирования, но с разным количеством отрезков разбиения. Предусмотреть построение графика первообразной функции на заданном интервале.
1.Теоретическая часть.
МЕТОД ТРАПЕЦИЙ
![]()

![]()
![]() График функции y=f(x) представляется в виде ломанной,
соединяющей точки (Xi,Yi).
График функции y=f(x) представляется в виде ломанной,
соединяющей точки (Xi,Yi).
В этом случае площадь всей фигуры
Y (криволинейной трапеции) складывает-
ся из площадей элементарных прямо-
![]() (Xi,Yi)
линейных трапеций.
(Xi,Yi)
линейных трапеций.
Площадь каждой такой трапеции
равна произведению полусуммы
![]() оснований на высоту:
оснований на высоту:
Yi-1 (Xi-1,Yi-1) Yi
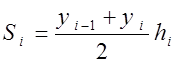 , i=1, 2,…n. (1)
, i=1, 2,…n. (1)
Xi-1 Xi X
Таким образом 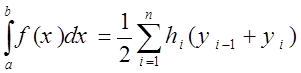 (2)
(2)
Частный случай рассмотренных формул является их применение при численном интегрировании с постоянным шагом
hi=h=const (i=1,2,…n)
Формулы (1) и (2) в этом случае принимают вид
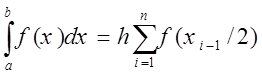
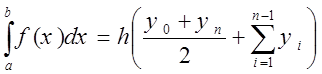
![]()
![]()
|
|


 |
|||
 |
|||
 |
|||||||||
 |
|||||||||
 |
|||||||||
 |
|||||||||
 |
|||||||||

![]()
 |
|||||
 |
|||||
|
|||||
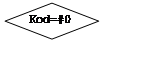
![]()
![]()
![]()
![]()
 |
|||
![]() 1 2 3 4 5 6
1 2 3 4 5 6
 |
 |
||
3.Входные и выходные данные (какие переменные используются в структуре и что обозначают)
Входные данные: вводятся границы отрезка [а; в] и количество отрезков разбиения n, затем рассчитывается h=(b-a)/n - длина отрезка разбиения. I i– это величина i-ой площади трапеции.
Выходные данные: I=h*((Ya+Yb)/2+I) – значение интеграла полученное методом трапеций.Ya, Yb- значение функции на концах отрезка
d=perv(b)-perv(a) – значение интеграла полученного по формуле Ньютона-Лейбница. perv(a), perv(b) – значение первообразной на концах отрезка
Заключение.
Если интервал разбиения от [0,3] и разбивается на 3 части, то программа выдаст результат вычисленный методом трапеций
y= 2,26431
Результат полученный по формуле Ньютона – Лейбница
y= 2,45674
Если же ввести тот же интервал разбиения, но количество отрезков на которые разбивается интервал 999, то программа выдаст такие результаты:
Методом трапеций
y=2.45671
Результат полученный по формуле Ньютона – Лейбница
y= 2,45674
И построит следующий график:
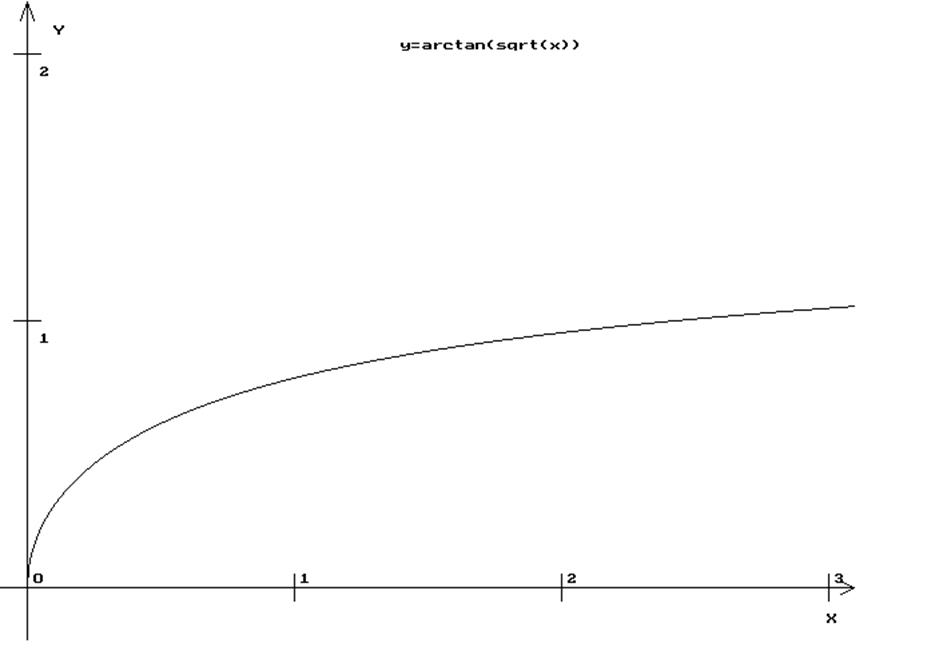
Приложение.
program shnaga;
uses Crt,Dos,graph;
Label 1,2;
{*************************************************************************}
procedure about;
begin
clrscr;
window(10,3,73,20);
textcolor(white);
clrscr;
gotoxy(21,1);
textcolor (12);
writeln('<-> О программе <->');
textcolor (15);
writeln(' Программа "SHNAGA" написана на языке Turbo Pascal v 7.0.',#10,#13,
'Такое название пришло на ум разработчику, когда тот поздними',#10,#13,
'октябрьскими вечерами настойчиво пытался сделать прогу по',#10,#13,
'информатике. И вот что у него вышло...(см. п."Решение" и',#10,#13,
'п."График")');
writeln;
writeln(' Если Вы хотите объявит слова благодарности разработчику,',#10,#13,
'либо сообщить о недостатках программы, то.......пишите',#10,#13,
'письма: student_upi@mail.ru');
writeln;
writeln(' [1] Все права защищены ',#10,#13,
' Бесплатная лицензия для граждан',#10,#13,
' и организаций России.',#10,#13,
' Сделано в России.');
textcolor(0);
readln;
end;
{*************************************************************************}
procedure zadanie;
begin
clrscr;
window(10,3,73,20);
textcolor(white);
clrscr;
gotoxy(21,1);
textcolor (12);
writeln('<-> Задание <->');
textcolor (15);
writeln(' Тема: "Приближенное вычисление определённого интеграла',#10,#13,
' методом трапеций."');
writeln;
writeln(' Условие задачи: ',#10,#13,
' В программе предусмотреть возможность вычесления зна-',#10,#13,
'чения интеграла по заданному количеству отрезков разбиения',#10,#13,
'интервала интегрирования. Для проверки правельности программы',#10,#13,
'предусмотреть вывод точного значения интеграла, вычеслнного по',#10,#13,
'формуле Ньютона-Лейбница. Вычисления производить для того же ',#10,#13,
'интервала интегрирования, но с разным количеством отрезков.',#10,#13,
'Предусмотреть построение графика первообразной функции на',#10,#13,
'заданном интервале.');
textcolor(0);
readln;
end;
{****************************************************************************}
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.